基于相对高程异常的GPS高程拟合方法探讨
2014-07-02陈艳红马全明刘瑞敏毛晓康
陈艳红,马全明,刘瑞敏,毛晓康
(1.石家庄经济学院,河北 石家庄 050031;2.北京城建勘测设计研究院有限责任公司,北京 100101;3.中南大学,湖南 长沙 410083)
基于相对高程异常的GPS高程拟合方法探讨
陈艳红1,马全明2,刘瑞敏2,毛晓康3
(1.石家庄经济学院,河北 石家庄 050031;2.北京城建勘测设计研究院有限责任公司,北京 100101;3.中南大学,湖南 长沙 410083)
在传统二次曲面GPS高程拟合的基础上,提出一种基于相对高程异常的GPS高程拟合方法。该方法首先通过相对正常高高程异常值的改正,把GPS点的相对大地高转化为相对正常高,然后将相对正常高与已知点的正常高高程连算,按照传统的水准测量计算方法平差解算,即能得到最优解的正常高。采用某山区工程实例数据进行了验证,表明该方法在地势起伏较大的测区比二次曲面拟合得到的精度要高。
大地高;正常高;GPS高程拟合;高程异常
一、引 言
近年来,GPS卫星定位技术已在测绘领域得到广泛应用,它不仅能获取高精度的平面位置,而且能获得高精度的大地高,如果将大地高转换为我国采用的正常高,代替部分的传统水准作业,具有较大的经济效益[1]。
目前,对GPS高程数据进行转换的常用方法有物理重力法和几何解析法两种。在实际工程应用中,由于无法获得必要的重力数据,故重力法难以普及[2]。因此,在工程应用中以几何解析法居多,其主要包括解析多项式法、加权均值法、多面函数法及近年来非常流行的神经网络法等[3-10]。这些 GPS高程拟合方法的精度受到联测水准点在测区的分布情况和数量的限制,只考虑了高程异常与点的位置间的关系,而没有考虑高程异常与点的高程间的关系。本文在GPS高程拟合时不仅考虑高程异常与位置的关系,以及与大地高的关系[11],并提出了基于相对正常高高程异常的GPS高程拟合模型。
二、基于相对正常高高程异常的GPS高程拟合原理
由于原有GPS高程拟合精度受到联测水准点在测区的分布情况和数量的限制,只考虑到高程异常与点的位置有关,而没有考虑到高程异常与点的高程的关系。因此本文在传统二次曲面GPS高程拟合的基础上,不仅考虑高程异常与位置的关系,还考虑与相对大地高的关系。
原有GPS高程拟合思路是先求出高程异常ζ,然后把大地高转化为正常高。本文在拟合时不求高程异常ζ,而是先把GPS点的相对大地高转化为相对正常高,须加一个改正数,即相对正常高高程异常值。在得到相对正常高高程后,再与已知点的正常高高程连算,按照传统的水准测量计算方法平差解算,就能得到最优解的正常高。
1.GPS相对大地高高程转化为相对正常高高程
将GPS大地高程数据转化为水准测量的相对正常高高程Δh0,即

式中,HA、HB分别表示A、B两点的大地高,大地高即GPS数据中的高程数据;分别表示A、B两点的正常高,即我国使用的高程系统;ΔhAB表示A点到B点的相对大地高,即 A、B两点的大地高差;表示A点到B点的相对正常高高差,即A、B两点正常高高差;ζAB表示A点到B点的相对正常高高程异常,即A、B两点的高程异常值的差值。
从式(1)中可以看出,只要得到两点的相对正常高高程异常ζAB,就可以把GPS大地高程数据转化为两点的相对正常高,再根据两点的相对正常高和已知点的正常高进行连算,利用间接平差进行计算,就可以得出测区所有点的正常高高程,把GPS大地高转化为正常高高程。
2.相对正常高高程异常求解
(1)建立相对正常高高程异常ζij模型
根据相对正常高高程异常ζij不仅与点的位置有关系,还与相对大地高有关,建立如下函数模型

式中,ζij表示i点到j点的相对正常高高程异常,ζij=ζj-ζi;Δhij表示i点到j点的相对大地高高程,Δhij=Hj-Hi;(Xj,Yj)表示j点平面坐标。
在测区中选定一个起始点,所有点的相对正常高高程异常都是基于这一个点的。这个起点最好选在测区的中间。
为了便于拟合计算,对上面的函数模型具体化,ζij与Δhij、Xj、Yj多项式关系为

式中,Ki(i=0,1,…,n+m+1)为系数。
对于不同的测区,根据已知数据来选择系数Ki的个数。
(2)相对正常高高程异常ζij的求解
利用已知点的平面坐标、大地高和正常高的数据按最小二乘法求解系数K。根据式(4)计算未知点的相对正常高高程异常的步骤如下:
1)明确测区已知点的个数,来确定式(4)中的系数K的个数,K的个数要少于已知点的个数。
2)在测区里选定一个起始点,计算其他已知点相对起始点的相对大地高高程、相对正常高高程和相对正常高高程异常,再利用间接平差按最小二乘法求解系数K。
3)计算待拟合点相对于起始点的相对大地高Δh起始点到未知点,然后代入式(4)中可求得待拟合点相对起始点的相对正常高高程异常。
3.GPS相对大地高转化为相对正常高
求解待定点相对于起始点的相对正常高高程异常后,通过式(2)求得待定点相对起始点的相对正常高,即
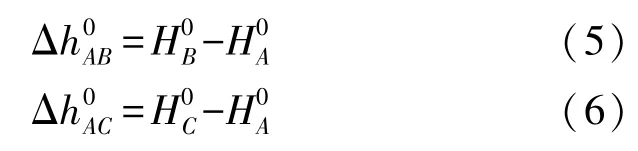
利用式(5)—式(6)就可以得到B、C两点的相对正常高。这样就能把待定点相对于起始点的相对正常高转化为任意两个待定点间的相对正常高。
4.相对正常高求解正常高高程
求得的两点间相对正常高和已知点的正常高高程数据按下列公式计算就得到待定点的正常高高程。

上式求出的待定点的正常高高程,由于待定点可以由不同的已知点来推求,这样就存在多余观测数据,利用平差计算优化待定点的正常高高程解。
三、实例数据分析
为了验证相对正常高高程异常的GPS高程拟合方法的可行性,本文采用二次曲面拟合的方法进行比较验证。某山区测区控制点共有15个,控制点的示意图如图1所示,在该区选取了平均对称的7个已知点,具体数据见表1,其余8个点作为待拟合点,具体数据见表2。
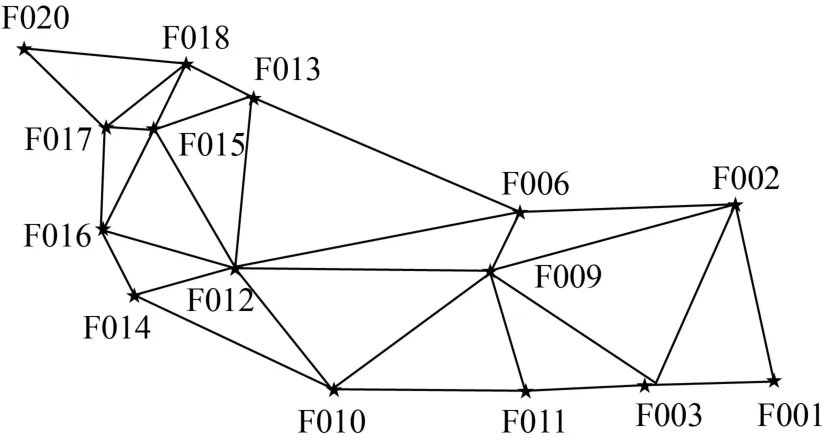
图1 山区GPS控制点示意图

表1 7个已知点的数据 m
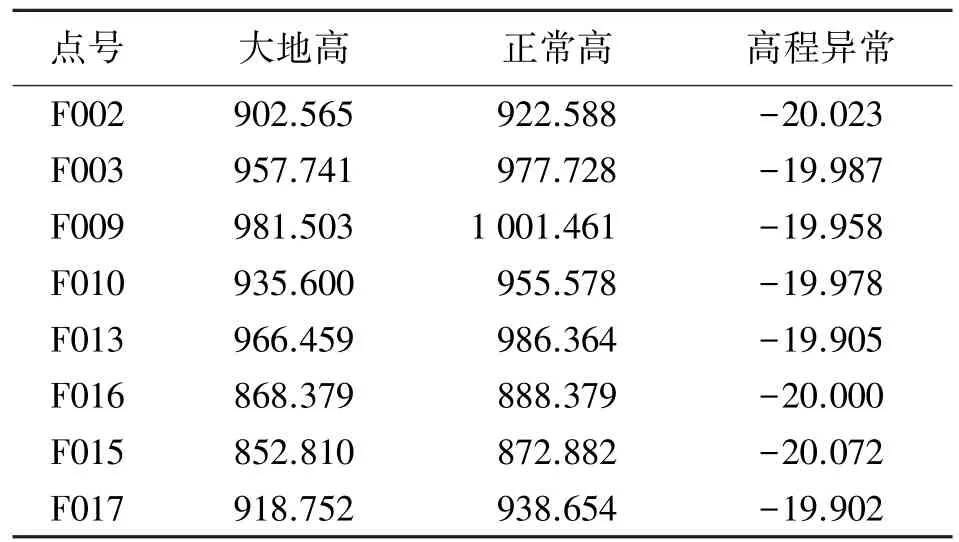
表2 8个待拟合点的数据 m
1.利用二次曲面进行GPS高程拟合
采用二次曲面拟合,用Matlab 7.0实现其算法,得到了8个待拟合点的正常高(见表3),内部符合
精度为1.4 cm,外部符合精度为23.0 cm。

表3 二次曲面拟合结果
2.基于相对正常高高程异常的GPS高程拟合
选取F012作为起始点,根据待拟合点和已知点组合的控制网模型,列出间接平差方程,求解待拟合点的正常高见表4,其内部符合精度为4.3 cm,外部符合精度为2.74 cm。3.二次曲面拟合与相对正常高高程异常拟合对比

表4 8个待拟合点结果
由表3、表4可以明显地看出,利用相对正常高高程异常的GPS高程拟合得到的待定点的精度好于传统的二次曲面拟合,其最大的残差为4.2 cm。测区的GPS点之间的平均边长在2 km左右,最大残差为4.2 cm,在普通几何水准测量误差允许残差范围内。在地势起伏较大的地区应用二次曲面拟合,其精度有的很差。从表中可以看出,二次曲面拟合的内符合精度很高但外符合精度很低,这是由于山区的高程异常变化大所决定的。
通过对比,充分地说明了基于相对正常高高程异常的GPS高程拟合在处理山区的数据时能明显地提高GPS高程拟合的精度。
四、结束语
传统的GPS高程拟合依赖于已知点平面位置数据,而没有考虑到高程异常值与地面高低起伏之间的关系。本文在进行高程拟合时不仅考虑了高程异常与平面的位置间的关系,而且还考虑了与地面的起伏高差之间的关系,在传统二次曲面GPS高程拟合的基础上,通过增加一个相对大地高拟合变量,提出了基于相对正常高高程异常的GPS拟合方法,并通过某山区工程实例验证了此方法的可行性,同时也验证了采用此方法的拟合精度比传统二次曲面的GPS高程拟合精度要高。
[1] 张正禄,邓勇,罗长林,等.利用GPS精化区域似大地水准面[J].大地测量与地球动力学,2006,26(4):14-17.
[2] 张小红,程世来,许晓东.基于Kriging统计的GPS高程拟合方法研究[J].大地测量与地球动力学,2007,27(2):47-51.
[3] 杨江波,李为乐,余代俊,等.GPS高程拟合方法的实验研究[J].测绘科学,2009,34(3):54-57.
[4] 黄祥雄,廖超明,曾教胜,等.区域精化似大地水准面在工程三维GPS控制网建设中的应用研究[J].测绘通报,2010(2):35-37.
[5] 杨明清,靳蕃,朱达成,等.用神经网络方法转换GPS高程[J].测绘学报,1999,28(4):301-307.
[6] 刘俊领,刘海生,王衍灵,等.GPS高程拟合方法研究[J].测绘与空间地理信息,2009,32(1):143-147.
[7] 魏立峰,何建国.GPS高程拟合似大地水准面的方法[J].地理空间信息,2010,8(4):72-73.
[8] 李秀海.平坦地区GPS高程拟合方法精度分析[J].黑龙江工程学院学报:自然科学版,2009,23(4):4-6.
[9] 陈本富,王贵武,沈慧,等.基于Matlab的数据处理方法在GPS高程拟合中的应用[J].昆明理工大学学报:理工版,2009,34(5):1-4.
[10] 高宁,高彩云,吴良才.GPS高程迭加拟合模型的研究[J].西安科技大学学报,2009,29(3):339-343.
[11] 吴晓平.似大地水准面的定义及在空中测量中涉及的问题[J].测绘科学,2006,31(6):24-25.
Discussion on the Relative Height Anomaly of GPS Elevation Fitting Method
CHEN Yanhong,MA Quanming,LIU Ruimin,MAO Xiaokang
P228.4
B
0494-0911(2014)12-0067-03
陈艳红,马全明,刘瑞敏,等.基于相对高程异常的GPS高程拟合方法探讨[J].测绘通报,2014(12):67-69.
10.13474/j.cnki.11-2246.2014.0400
2014-01-08
陈艳红(1977—),女,河北阜城人,硕士,讲师,主要从事大地测量数据处理的研究与工作。
