基于BG理论确定Phillips方法的正则化参数并评价反演结果

高 阳,肖立志,谢庆明

(1.中国石油大学理学院,北京102249;2.中国石油大学地球物理与信息工程学院北京102249; 3.重庆地质矿产研究院国土资源部页岩气资源勘查重点实验室,重庆400042)

基于BG理论确定Phillips方法的正则化参数并评价反演结果

高 阳1,肖立志2,谢庆明3

(1.中国石油大学理学院,北京102249;2.中国石油大学地球物理与信息工程学院北京102249; 3.重庆地质矿产研究院国土资源部页岩气资源勘查重点实验室,重庆400042)

正则参数的选取在Phillips-Twomey方法中起着关键性的作用,但一方面人们很难确定该参数的选取是否恰当,另一方面在参数选取时存在着很大的主观因素。研究利用Phillips-Twomey方法反演核磁共振横向弛豫时间谱时正则参数的确定,其确定方法是基于BG理论中的折中准则和正则参数最小准则;同时,还利用分辨率矩阵和协方差矩阵来评价反演所得横向弛豫时间谱。数值模拟和岩心分析均表明,基于BG理论的折中准则和正则参数最小准则方法适用于确定Phillips-Twomey方法反演核磁共振横向弛豫时间谱的正则参数r的选取。岩心分析结果表明,该方法反演效果比常规的SVD方法好,并且该方法避免了反演者的主观判断,因此反演结果没有反演者个人偏好影响。

核磁共振测井;Phillips-Twomey方法;分辨率矩阵;协方差矩阵;折中准则

Backus-Gilbert线性评价理论(即BG理论)[1-2]的核心是展布准则和折中准则[3-4]。目前已经有学者将BG理论中的分辨率矩阵和协方差矩阵应用到反演当中[3]。Phillips-Twomey方法在地球物理反演和核磁共振反演中都有着非常重要的作用[5-9],而正则参数r的选取往往是根据反演者的经验,使得反演结果带有反演者的主观判断。基于此,笔者引入BG理论中的折中准则。对正则参数r的不同取值分别计算出分辨率矩阵和协方差矩阵,再算出展布和协方差矩阵的模,利用折中准则和r值最小准则确定正则参数r。同时尝试利用BG理论评价核磁共振测井反演结果,确定反演结果的可信度。

1 Phillips-Twomey方法及其折中解

1.1 Phillips-Twomey方法

核磁共振测井多指数反演结果的好坏直接影响到有关岩石储集物性及流体特性参数的计算[10-15],该反演实际上是解超定线性方程组[16-17]Gm=d,其中G为M×N矩阵,m为N维列向量,d为M维列向量。假设d有误差δd。由于系数矩阵G的条件数很高——在核磁共振测井中G的条件数可能达到1015数量级,造成d的微小误差在m中都会被放大得很大,使得该问题严重不适定。Phillips-Twomey方法认为解应该是最光滑的,即解的二阶导数的模长应该最小。因此Phillips-Twomey方法定义光滑度量

并求s(m)在约束条件δd=Gm-d下的极小值点。由于误差项δd未知,只能要求‖δd‖=‖Gm-d‖尽量地小。 因此,定义E(m)=rs(m)+‖Gmd‖2,并将E的极小值点m^作为线性方程组Gm=d的解。其中r为正则化参数或权重参数,决定两部分在E中所占比重。 令有

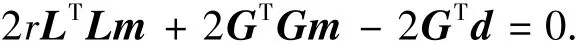
因此解m^=(GTG+rLTL)-1GTd。 此时,G的广义逆G-g=(GTG+rLTL)-1GT。

1.2 正则参数对反演结果的影响

在Phillips-Twomey方法中,正则参数r的选取是十分关键的。 随着r的增大,s(m)所占的比重增大,所得解就越光滑,但由于此时误差项δd所占的比重相应减小,因此原方程组在中所占的比重也减小;相应地,若r减小,δd所占的比重增大,原方程组在中所占的比重也增大,但这时s(m)所占的比重减小,因此所得解可能不够光滑。 如果r值选择不当,不管是过大还是过小,都会导致反演结果失真。图1说明了正则参数r的选取对反演结果的影响。从图中可以看出,恰当的r值为3,过大(如图中r= 10)或者过小(如图中r=0.5)都会导致反演结果失真。 考虑到反演的任务是解方程组,原方程组应起主要作用。 因此在保证解足够光滑的情况下,r值选取应尽量小,并称这一准则为r值最小准则。

1.3 正则参数的选取

按照BG理论,如果线性方程组Gm=d的广义逆为G-g,则分辨率矩阵R=G-gG,协方差矩阵cov[m]=σ2G-g(G-g)T[1-4],这里假设d的误差在统计上是独立的且它们有相同的方差σ2。 核磁共振测井仪器的设计可以保证误差独立。核磁共振测井所采集的回波串,经过相敏检波器可以分离为两道,一道是含噪声的回波串数据,一道是纯噪声,这样就可以得到噪声的方差[18]。 在Phillips-Twomey方法中,给定一个r,就可以求得一个广义逆G-g= (GTG+rLTL)-1GT,也就可以得到分辨率矩阵和协方差矩阵。 图2所示为r=0,数据方差σ2=1时的分辨率矩阵和协方差矩阵。

由图2可以看出,分辨率矩阵比较接近单位矩阵,分辨率最佳。这是因为=G-gd=G-g(Gm)= (G-gG)m=Rm。当R=I时,=m,即就是模型m。当R≠I时,的某个分量,它不仅与mj有关,而且还与其他的mi有关,实际上,它是模型m的一个加权平均。 因此,可以用矩阵R与单位矩阵I的相似程度来衡量的好坏。R与I越接近,与m越接近,就越好;反之,就越坏。在实际应用中,一般用矩阵R-I的L2模来衡量分辨率矩阵,并称它为矩阵R的非对角元素的展布。

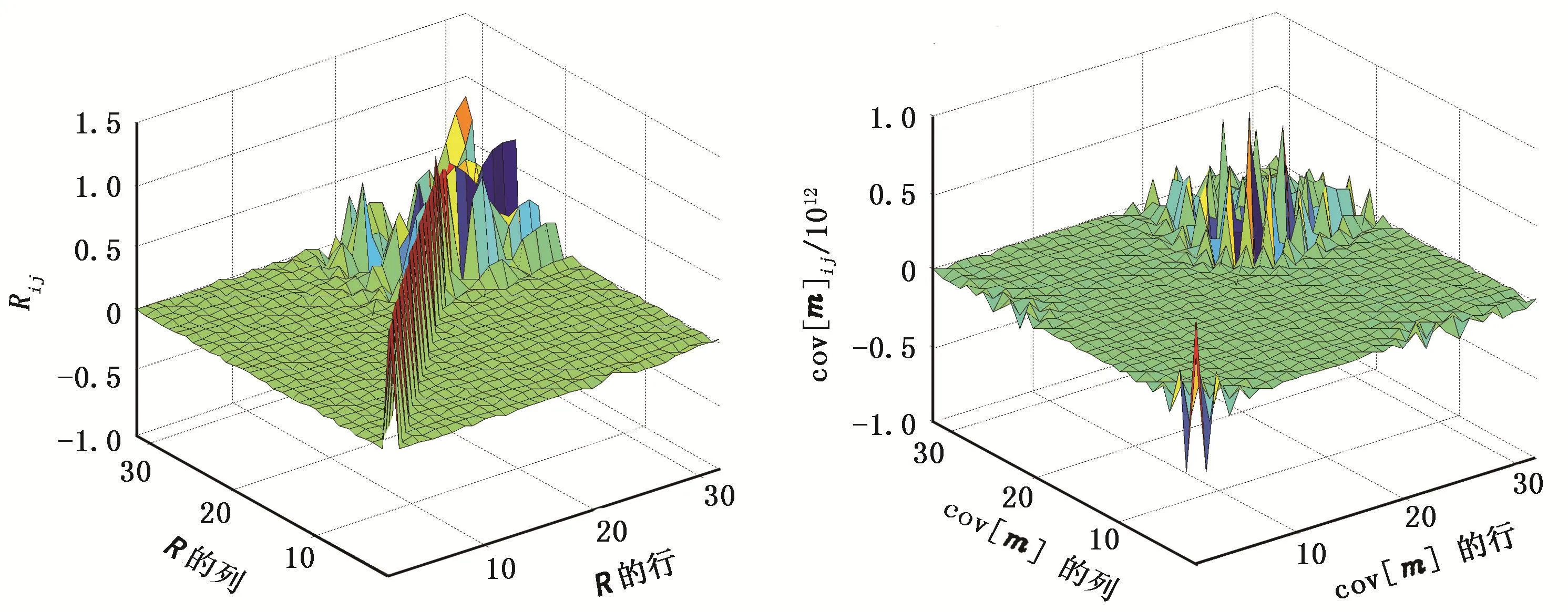
图2 r=0,σ2=1时的分辨率矩阵(左)和协方差矩阵(右)Fig.2 Resolution matrix and covariance matrix when r=0 and σ2=1

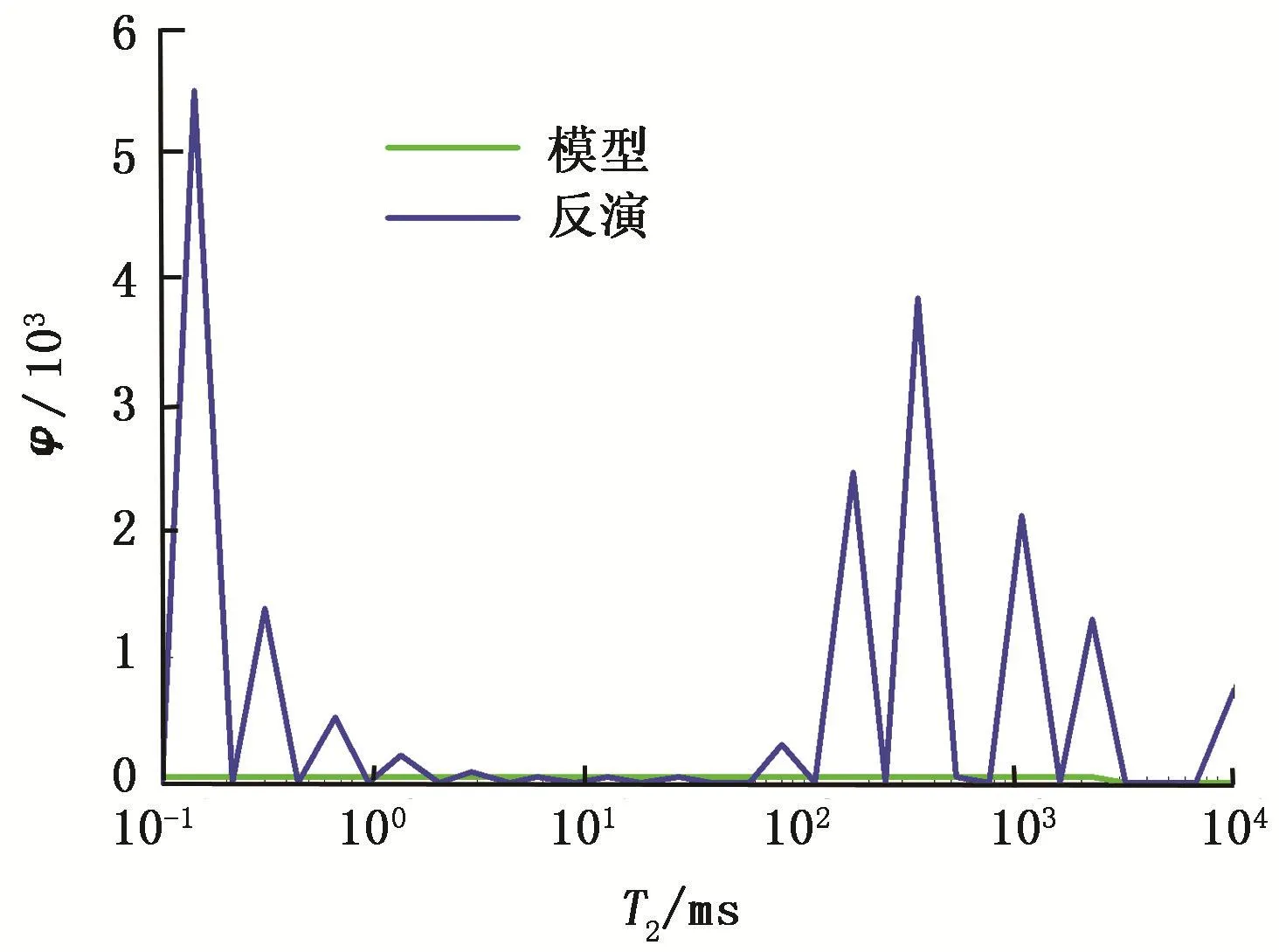
图3 r=0,σ2=1时的反演结果与模型对比Fig.3 Comparison of inversion result and model when r=0 and σ2=1

由于r=0,m^=(GTG)-1GTd,实际上就是最小方差解[2],因此是没有正则化的解。 没有正则化的解与真实解必然相距甚远,图3也正说明了这一点。

通过将r增大来观察模型分辨率矩阵和协方差矩阵。 图4是r=0.01,数据方差σ2=1时的模型分辨率矩阵和协方差矩阵。此时的模型分辨率矩阵与单位矩阵差别比较明显,说明分辨率减小了。同时,协方差矩阵的数量级已经从1012降低到了100,说明方差明显改善。但是这是以牺牲分辨率为代价的。从分辨率矩阵和协方差矩阵的变化看,这种牺牲还是值得的,因为这是以较小的分辨率为代价换取较大方差的改善。图5是r=0.01,数据方差σ2=1时,模型m与反演结果的对比。与图3相比,反演结果与模型接近了许多,也说明了这种以牺牲分辨率为代价换取方差的改善是值得的。当然,从图中也可以看到,小弛豫分量反演结果与模型相差还是很大,因此这还不是理想结果。BG折中理论中的最佳折中解是以牺牲最小分辨率为代价换取最大方差减小的解。

实际上,要使分辨率高,就要使模型分辨率矩阵与单位矩阵差别小,即小;要使解的误差小,就要使小。BG理论认为分辨率和协方差是一对矛盾,二者不可兼得,只能取折中:要么牺牲一定的分辨率来换取协方差的减小,要么以较大的协方差来获得较高的分辨率。这就是BG折中理论的核心思想。

图6所示为Phillips-Twomey方法中随r值的增加,spread(R)和的变化。

随着r的增加,展布越来越大,即分辨率越来越低;但是方差却越来越小。 这再一次说明要使spread(R)和同时达到极小是不可能的,因此BG折中理论定义

并对ε取极小。 此时的r值即为最佳折中解所对应的r值。 为了确定哪一个r值使得ε取极小,可以做ε-r关系图(图7)。

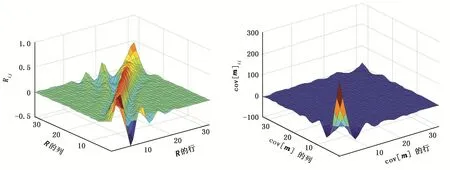
图4 r=0.01,σ2=1时的模型分辨率矩阵(左)和协方差矩阵(右)Fig.4 Resolution matrix and covariance matrix when r=0.01 and σ2=1

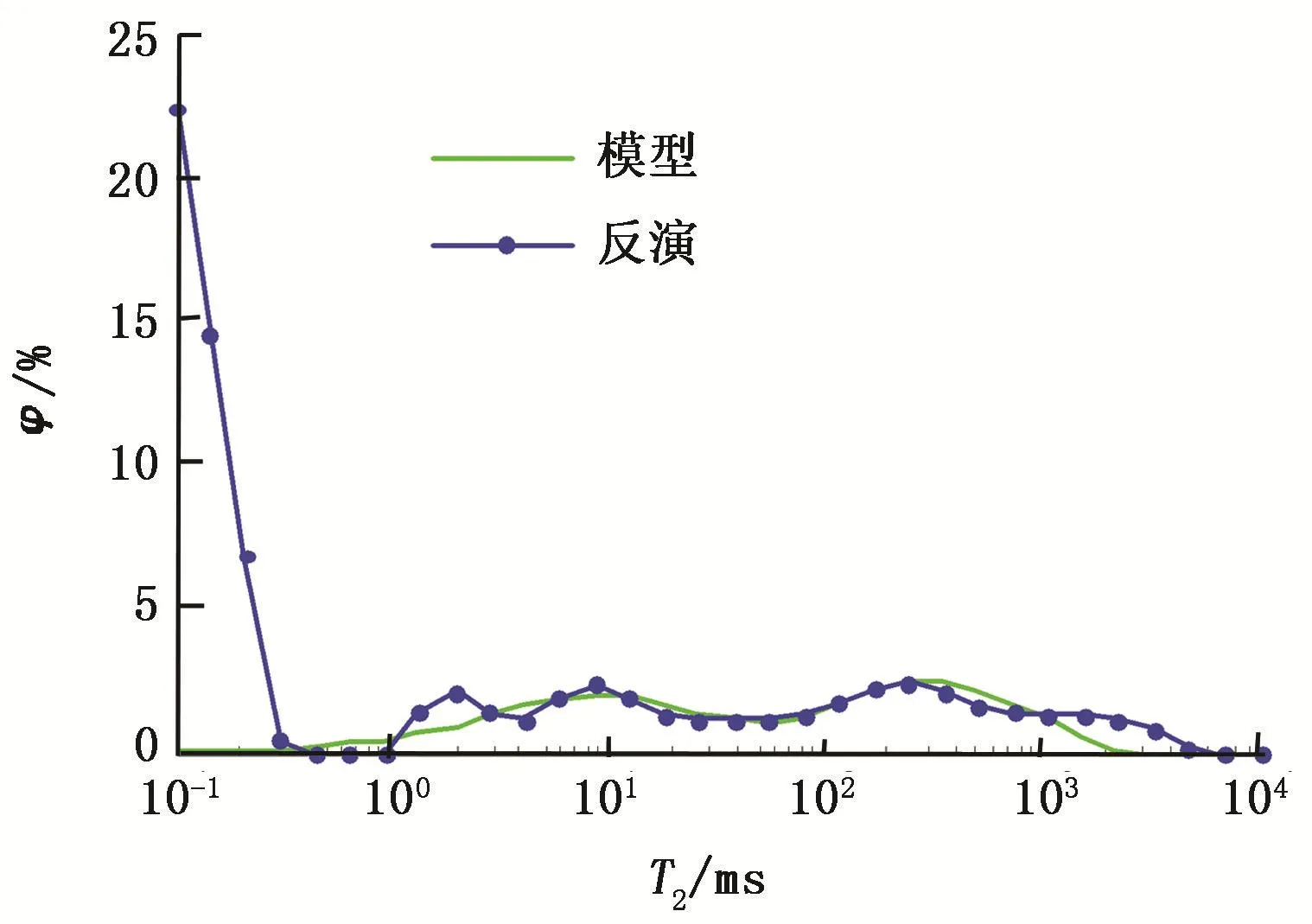
图5 r=0.01,σ2=1时的反演结果与模型对比Fig.5 Comparison of inversion result and model when r=0.01 and σ2=1

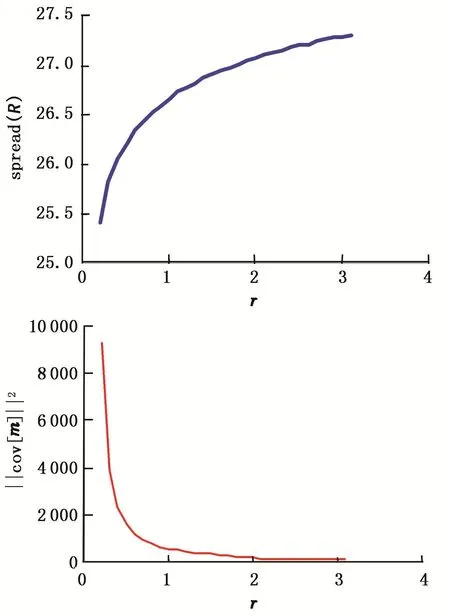
图6 spread(R)和‖cov[m]‖与r的变化关系Fig.6 Variaion of spread(R)and‖cov[m]‖with r

如图7所示,点A即为ε取极小的点即最佳折中点,但曲线在A点附近极为平滑,因此虽然B、C两点距离A点较远,但是它们的ε值与A点相差甚微。考虑到r值选取应尽量的小,结合折中准则和r值最小准则,定义

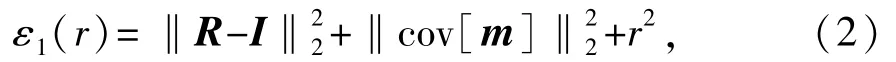
并对其求最小,将此时的r值确定为Phillips-Twomey方法所需要的r值。图8是利用最佳折中准则和r值最小准则确定Phillips-Twomey方法的正则参数r,反演不同信噪比(rSN)回波串得到的T2谱。

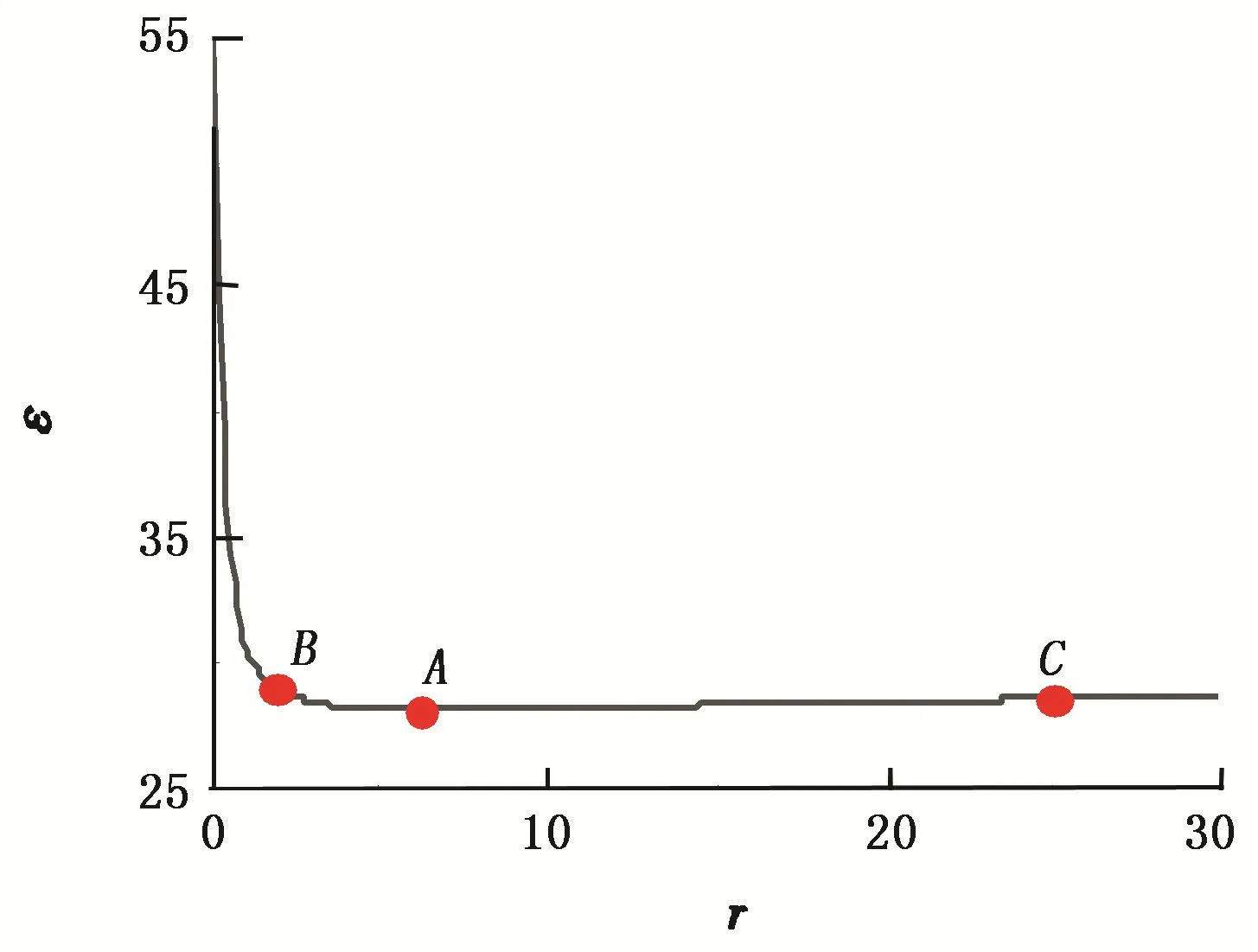
图7 ε-r关系图Fig.7 ε-r curve

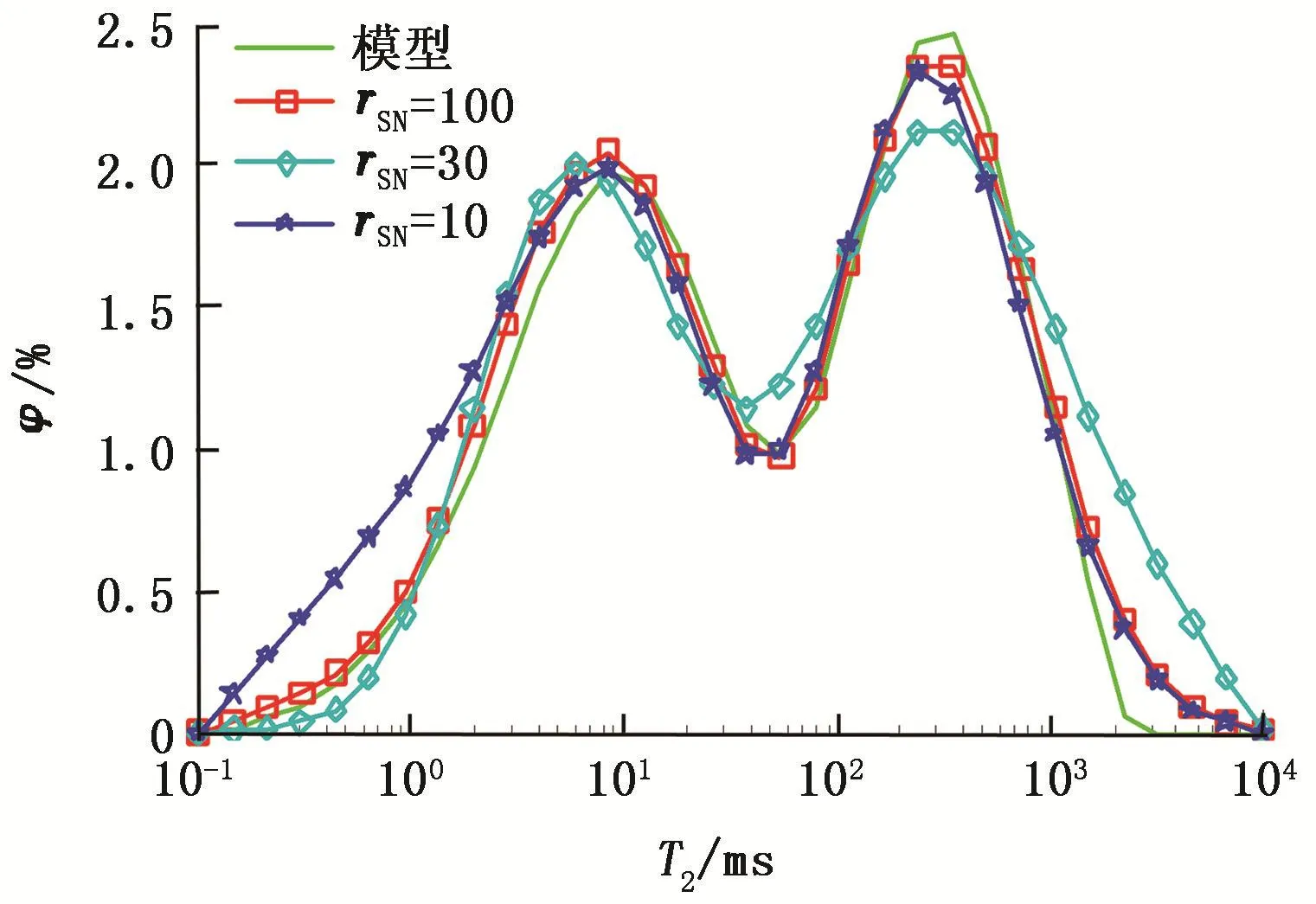
图8 不同信噪比回波串反演结果Fig.8 Inversion results of echoes with different rSN

2 反演结果评价

由图8可以看出,对于不同的信噪比来说,反演结果与模型相当符合,说明反演结果非常好。但在核磁共振测井反演时,并不知道真实的T2谱是怎样的。此时对反演结果的评价可以通过分辨率矩阵和协方差矩阵来实现。

图9是信噪比rSN=100,r=1.7时的分辨率矩阵和协方差矩阵。从整体上看,分辨率矩阵是对角占优矩阵,虽然对角线上的值小于0.3,但对角线及其前后两个的值加起来大部分都大于0.6(理论上R的行和应该为1,由于在做非负约束时磨平了系数矩阵,使得R有些行和不为1,这是导致不是所有的值都大于0.6的主要因素)。以R的第18行为例,最大值在第18列为0.2836,这说明m18是18的主要贡献者;而且第18行的第17列和第19列分别为0.2384和0.245 2,这三者加起来为0.769 2。因为T2谱是连续的,所以m17、m19与m18非常接近。从这个角度考虑,可以认为m18的贡献为0.7692。因此从分辨率矩阵的角度看,此次反演的可信度是比较高的。再从协方差矩阵看,绝对值最大值为0.0223,最小值几乎为0,而信号噪声的标准差为0.2947,这说明该方法明显地压制了信号的噪声。因此,此次反演的误差也是相当小的。

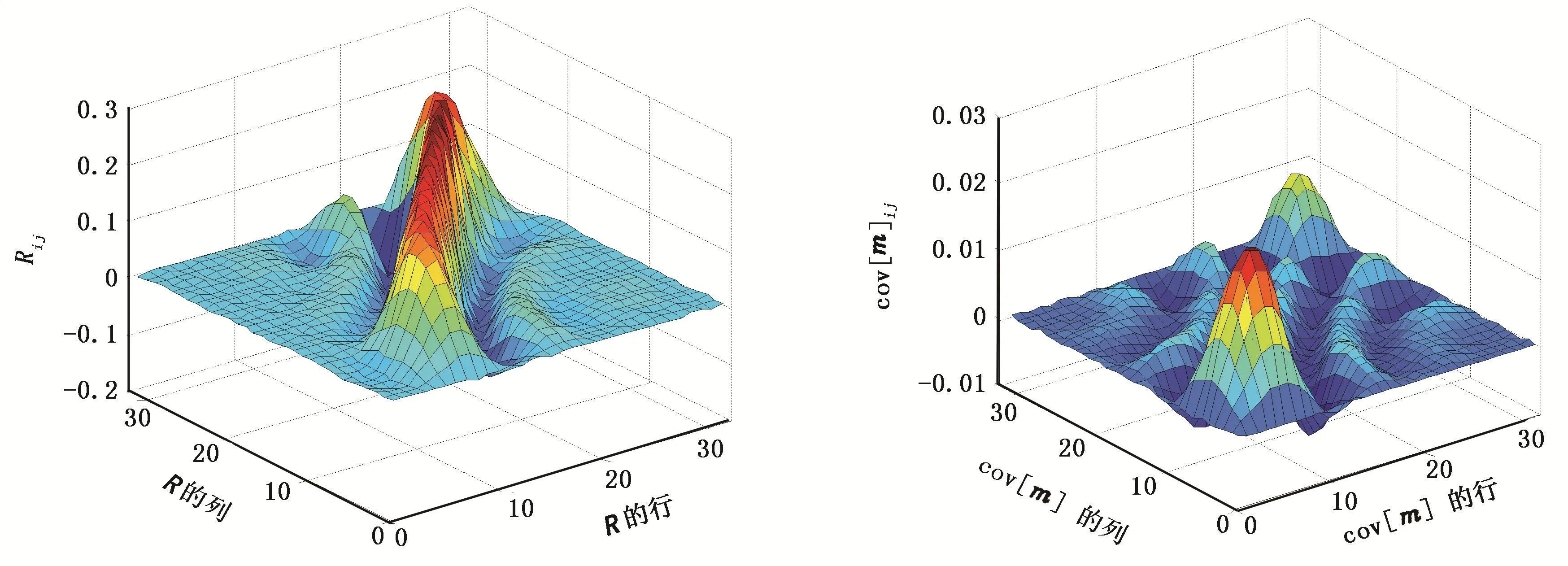
图9 rSN=100,r=1.7时的模型分辨率矩阵(左)和协方差矩阵(右)Fig.9 Resolution matrix and covariance matrix when r=1.7 and rSN=100

3 NMR岩心资料处理

图10是根据折中准则和r值最小准则反演某地区3块岩心所得T2谱(图中标有PH-T字样的曲线)和用SVD方法得到的T2谱(图中标有SVD字样的曲线)对比。这3块岩心都是碳酸盐岩,孔径比较大,岩石孔隙度也相对较大,这一点从反演得到的T2谱也可以看出。根据资料,确定束缚水的T2截止值为92 ms,泥质束缚水的T2截止值为4 ms[11-12]。

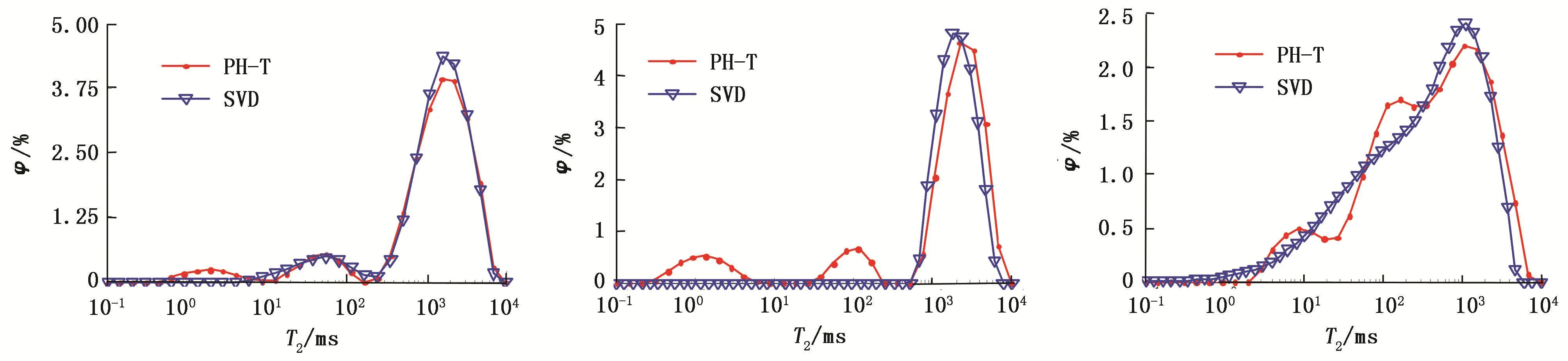
图10 岩心反演T2谱Fig.10 Inversed T2spectrums of cores

从图中可以看出,两种反演方法在长弛豫时间上基本一致。在短弛豫方面,用SVD方法得到的第一块岩心的T2谱只能反映出毛管束缚水,第二块岩心的T2谱根本不能反映出束缚水信息;而根据折中准则和r值最小准则,得到的这两块岩心的T2谱都可以清晰地分辨出泥质束缚水和毛管束缚水。由此可知,在短弛豫方面根据折中准则和r值最小准则得到的T2谱具有一定的优势。对于第三块岩心,两种方法反演的结果差别不大,说明本方法也不是每次都比SVD方法好。

图11是第一块岩心在上述r值下的分辨率矩阵和协方差矩阵。分辨率矩阵的峰值基本上都在对角线上,且峰值较高;同时协方差矩阵整体上来说值是比较小的,最大值没有超过0.04。因此,这次反演的可信度还是比较高的。

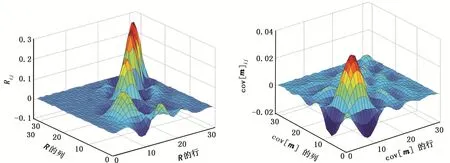
图11 第一块岩心的分辨率矩阵(左)和协方差矩阵(右)Fig.11 Resolution matrix and covariance matrix of the first core

4 结 论

(1)数值模拟和岩心分析均表明基于BG理论的折中准则和r值最小准则方法适用于确定Phillips-Twomey方法反演核磁共振横向弛豫时间谱的正则参数r的选取,且一般来说其效果比常规的SVD方法好。正则参数r的选取方法如下:首先对正则参数r的不同取值分别计算出分辨率矩阵和协方差矩阵,然后计算出分辨率矩阵和协方差矩阵的模,最后利用折中准则和r值最小准则确定正则参数r,即对公式(2)求极小。这样在选取r时,避免了反演者的主观判断,因此反演结果没有反演者个人偏好的影响。

(2)数值模拟所设定的地层岩性是砂岩,岩心分析中的岩心为碳酸盐岩,所以本文所述方法适用于砂岩和碳酸盐岩地层,对于其他常规储层,理论上是能够正确反演的。对于页岩等非常规储层,尚不清楚是否适用。

(3)利用BG评价理论评价核磁共振测井反演结果,确定反演结果可信度差别。其方法是看分辨率矩阵主峰是否都在对角线上,其他值是否接近0,协方差矩阵是否接近0矩阵。如果是,则反演结果比较好,反之则较差。如果想评价某一个分量,就看它所在的行是否满足上述条件。

[1] BACKUS G E,GILBERT J F.The resolving power of gross earth data[J].Geophysical Journal,1968,16(2): 169-205.

[2] BACKUS G E,GILBERT J F.Uniqueness in the inversion of inaccurate gross earth data[J].Philosophical Transactions,1970,266(1173):123-192.

[3] 王家映.地球物理反演理论[M].武汉:中国地质大学出版社,1998.

[4] 杨文采.地球物理反演的理论和方法[M].北京:地质出版社,1996.

[5] 肖立志,张恒荣,廖广志,等.基于Backus-Gilbert理论的孔隙介质核磁共振弛豫反演[J].地球物理学报, 2012,55(11):3821-3828. XIAO Li-zhi,ZHANG Heng-rong,LIAO Guang-zhi,et al.Inversion of NMR relaxation in porous media based on Backus-Gilbert theory[J].Chinese J Geophys,2012,55 (11):3821-3828.

[6] PHILLIPS D L.A technique for the numerical solution of certain integral equations of the first kind[J].J ACM, 1962,9:84-87.

[7] TWOMEY S.On the numerical solution of Fredholm integral equations of the first kind by the inversion of linear systems profuctuced by quadrature[J].J ACM,1963, 10:97-101.

[8] 高阳,肖立志,谢庆明.利用Phillips-Twomey方法对核磁共振弛豫测量结果的反演及其效果分析[J].西安石油大学学报:自然科学版,2012,27(5):32-38. GAO Yang,XIAO Li-zhi,XIE Qing-ming.Inversion of NMR transverse relaxation time using Phillips-Twomey method[J].Journal of Xiıan Shiyou University(Natural Science Edition),2012,27(5):32-38.

[9] 肖立志,于慧俊,刘化冰,等.新型核磁共振孔隙介质分析仪的研制[J].中国石油大学学报:自然科学版,2013,37(3):68-73.XIAO Li-zhi,YU Hui-jun,LIU Hua-bing,et al.A novel low field nuclear magnetic resonance analyzer for porous media[J].Journal of China University of Petroleum(E-dition of Natural Science),2013,37(3):68-73.

[10] MILLER A,CHEN S A.New method for estimating T2distributions from NMR measurements[J].Mag Re Imaging,1998,16:617.

[11] BUTLER J P,REEDS J A,DAWSON S V.Estimating solutions of first kind integral equations with nonnegative constraints and optimal smoothing[J].SIAMJ Numer Anal,1981,18(3):381-397.

[12] 葛新民,范宜仁,吴飞,等.岩石核磁共振T2谱与电阻率指数的对应性研究[J].中国石油大学学报:自然科学版,2012,36(6):53-56. GE Xin-min,FAN Yi-ren,WU Fei,et al.Correspondence of core nuclear magnetic resonance T2spectrum and resistivity index[J].Journal of China University of Petroleum(Edition of Natural Science),2012,36(6): 53-56.

[13] 王忠东,肖立志,刘堂宴.核磁共振弛豫信号多指数反演新方法及其应用[J].中国科学:G辑,2003,33 (4):323-332. WANG Zhong-dong,XIAO Li-zhi,LIU Tang-yan.New inversion method with multi-exponent and its application [J].Science in China(G),2003,33(4):323-332.

[14] 廖广志,肖立志,谢然红,等.孔隙介质核磁共振弛豫测量多指数反演影响因素研究[J].地球物理学报,2007,50(3):932-938. LIAO Guang-zhi,XIAO Li-zhi,XIE Ran-hong,et al. Influence factors of multi-exponential inversion of NMR relaxation measurement in porous media[J].Chinese J Geophys,2007,50(3):932-938.

[15] 谢然红,肖立志,张建民,等.低渗透储层特征及测井评价方法[J].中国石油大学学报:自然科学版, 2006,30(1):47-51. XIE Ran-hong,XIAO Li-zhi,ZHANG Jian-min,et al. Low permeability reservoir characteristics and log evaluation method[J].Journal of China University of Petroleum(Edition of Natural Science),2006,30(1):47-51.

[16] COATES G R,XIAO L Z,PRAMMER M G.NMR logging principles and applications[M].Texas:Gulf Publishing Company,1999.

[17] 肖立志.核磁共振成像测井与岩石核磁共振及其应用[M].北京:科学出版社,1998.

[18] 邓克俊.核磁共振测井理论及应用[M].东营:中国石油大学出版社,2010.

(编辑 修荣荣)

Evaluating regular parameter of Phillips method and assessing inversions based on BG theory

GAO Yang1,XIAO Li-Zhi2,XIE Qing-Ming3
(1.College of Science in China University of Petroleum,Beijing 102249,China; 2.College of Geophysics and Information Engineering in China University of Petroleum,Beijing 102249,China; 3.Key Laboratory of Shale Gas Exploration,Ministry of Land and Resources,Chongqing Institute of Geology and Mineral Resources,Chongqing 400042,China)

In the Phillips-Twomey method,it is essential to find a suitable regular parameter r.The selection of the parameter r remains practically difficult,and is often biased by researcherıs subjectivity.Finding a suitable regular parameter r in using Phillips-Twomey method to inverse nuclear magnetic resonance(NMR)logging transverse relaxation time was focused on.The way to finding the suitable r was based on the compromise criterion in BG theory and the r minimal criterion.The inversed transverse relaxation time was also assessed through the resolution matrix and the covariance matrix.Digital simulation and core analysis show that the approach in determining the regular parameter r of the Phillips-Twomey inverse method works very well for the inverse of NMR transverse relaxation time.Core analysis also shows that this method is better than the classical SVD method without subjective bias.

nuclear magnetic resonance logging(NMR logging);Phillips-Twomey method;resolution matrix;covariance matrix;compromise criterion

O 175.5

:A

1673-5005(2014)03-0050-07

10.3969/j.issn.1673-5005.2014.03.008

2013-10-11

中国石油大学(北京)科研基金资助(KYJJ2012-06-02);中国石油科技创新基金项目(2011D-5006-0307)

高阳(1979-),男,讲师,博士,主要从事核磁共振测井反演方法研究。E-mail:gaoyang1203@163.com。