试谈求函数值域的基本思想及方法

孔晓红

（甘肃省永靖县永靖中学，甘肃 永靖 731600）

试谈求函数值域的基本思想及方法

孔晓红

（甘肃省永靖县永靖中学，甘肃 永靖 731600）

本文简述了求函数值域（或最值）常用的基本方法函数的值域是研究函数不可缺少的一个重要方面。求函数值域是函数这部分内容的重、难点问题之一。求函数值域首先要考察定义域。以一次函数、二次函数、反比例函数、指数函数、对数函数、幂函数、三角函数等基本函数的图象和性质为基础，尤其要熟练掌握二次函数式在给定区间上值域的求法。应用化归思想、方程思想、相互制约思想、几何思想、基本不等式以及单调性、奇偶性、周期性等函数性质。

函数；值域；教学方法

一、求二次函数式在自然定义域上的值域，一般将函数式y=ax2+bx+c（a≠0）化为y=a（x-m）2+n的形式，这里化成这种形式体现两个优点：①知道图象的顶点坐标（m，n）、对称轴及函数最值；②函数的两个单调区间为（-∞，m]、[m，+∞）。这样，若a＞0，其值域为[m，+∞）；若a＜0，其值域为（-∞，m]

求二次函数式在限定区间D上的值域，先考察顶点横坐标m与区间D的关系。如果m∈D，那么一个最值就是n，再通过考察区间D的两个端点对应的函数值就能确定值域；如果m∉D，那么D必是函数的单调区间，利用单调性就能求出值域。

二、化归思想——通过替换或变形等方法把函数转化为基本函数式或基本函数有联系的形式，进而利用基本函数的图象和性质确定出值域

因此，可通过替换化归为幂函数后就可求出值域。

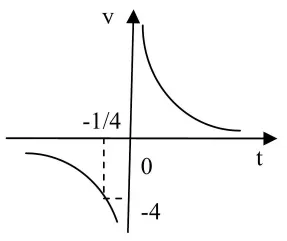
如图可知y≤-4或y＞0，∴函数的值域为（-∞，-4]∪（0，+∞）。

三、方程思想——一个函数式实际上就是关于自变量x与函数值y的方程，而根据函数的定义可知，这个方程必关于x有解，因此有时我们把函数式变形为关于x的方程后，利用方程有解的条件建立关于y的不等式关系，从而求出值域

【例3】：求函数y=log2ax+2logax+2的值域。

分析：把函数式视为关于x的方程，则这个方程关于x有解，因为x∈（0，+∞），所以logax∈R，这样把函数式看作关于logax的一元二次方程，那么这个方程恒有解，利用一元二次方程有解的条件就能求出值域。

解：因x＞0，∴logax∈R，设logax=t，则函数式可变形为t2+2t+（2-y）=0 由Δ=4-4（2-y）≥0解得y≥1，故函数的值域是[1，+∞）。

四、制约思想——自变量x与函数值y相互依存又相互制约。

分析：由于y受sinx的制约，而sinx∈（-1，1），因此从函数式解出sinx=f（y），通过-1≤f（y）≤1可求得值域。

分析：由于y受x2的制约，而x2≥0，因此从函数式解出x2=f（y），通过f（y）≥0能确定值域。

五、几何思想——几何思想即数形结合思想，通过作出函数的图象或根据函数式所表示的意义画出相应图形，进而求出值域

思路一：画出函数的图象，可观察出值域。思路二：由于|x-3|-|x+1|表示数轴上的点到3的距离与到-1的距离之差，因此，通过数轴可知值域是[-4，4]。

六、注意留意基本不等式即函数的单调性

【例7】：求函数y=x（3-2x），0＜x＜1的值域。

除以上基本思想方法外，要注意考察奇偶性与周期性。如果是奇函数或偶函数，我们只求正区间或负区间上函数值的范围，根据对称性就能确定值域；如果是周期函数，只求一周期区间上的值域。

总之，求值域是个较困难且较为灵活的问题，需灵活运用所学，灵活解决。

[1]史海平.一类函数值域的新求法[J].数学教学通讯，1989（05）.

[2]方亚娜.函数值域的求法[J].甘肃教育，1998（11）.

[3]李建标.关于函数值域的概念及其应用[J].中学教研（数学），2005（03）.

G623

A

1674-9324（2014）22-0100-02

孔晓红（1980—），女，甘肃永靖，现任中学一级教师。