求变力做功的方法

张志红

（天津市宝坻一中，天津 301800）

求变力做功的方法

张志红

（天津市宝坻一中，天津 301800）

变力做功问题综合性强，思维性强，知识面广，涉及的物理方法多，能力要求高，是高考的重难点之一。但无论是哪一类型的变力做功问题，都有相应的解题思路和方法。

微元法；等值法；平均力法；图像法；能量

功是中学物理的重要概念之一，它体现了力对物体的作用在空间上的积累，功尤其是变力做功是近年高考的热点，亦是考生应考的难点。但由于高中阶段所学的功的计算公式W=Fscosθ只能用于恒力做功，对于变力做功或物体运动轨迹是曲线的情况，就不能再用W=Fscosθ来计算。就此，总结如下几个求变力做功的方法。

一、力的大小不变，方向改变

1.等值法。若某一变力的功和某一恒力的功相等，则可以通过计算恒力的功，求出该变力的功。

例1：如图1，定滑轮至滑块的高度为h，已知细绳的拉力为F（恒定），滑块沿水平面由A点前进S至B点，滑块在初、末位置时细绳与水平方向夹角分别为α和β。求滑块由A点运动到B点过程中，绳的拉力对滑块所做的功。（忽略一切阻力）

解析：设绳对物体的拉力为T，显然人对绳的拉力F等于T。T在对物体做功的过程中大小虽然不变，但其方向时刻在改变，因此该问题是变力做功的问题。在忽略一切阻力的情况下，人对绳做的功就等于绳的拉力对物体做的功。而拉力F是恒力，所以F做的功可以用公式W=FScosa直接计算。由图1可知，在绳与水平面的夹角由α变到β的过程中，拉力F的作用点的位移大小为：

图1

2.微元法。当物体在变力的作用下作曲线运动时，若力的方向与物体运动的切线方向之间的夹角不变，且力与位移的方向同步变化，可用微元法将曲线分成无限个小元段，每一小元段可认为恒力做功，总功即为各个小元段做功的代数和。

图2

例2：如图2所示，某力F=10N作用于半径R=1m的转盘的边缘上，力F的大小保持不变，但方向始终保持与作用点的切线方向一致，则转动一周这个力F做的总功应为：

A.0J B.20πJ C.10J D.20J

解析：把圆周分成无限个小元段，每个小元段可认为与力在同一直线上，故ΔW=FΔS，则转一周中各个小元段做功的代数和为W=F×2πR=10×2πJ=20πJ，故B正确。

二、力的方向不变，大小改变

1.平均力法。若参与做功的力方向不变，而大小随位移线性变化，则可求出平均力等效代入公式W=Fscosθ求解。

2.图像法。若参与做功的力方向与位移方向始终一致而大小随时变化，我们可做出该力随位移变化的图像。如图3，那么图线下方所围成阴影部分的面积，即为变力做的功。

图3

例3：用铁锤将一铁钉击入木块，设木块对铁钉的阻力与铁钉进入木块内的深度成正比。在铁锤击第一次时，能把铁钉击入木块内1cm。击第二次时，能击入多少深度？（设铁锤每次做功相等）

解析：解法一：平均力法。

铁锤每次做功都用来克服铁钉阻力做的功，但摩擦阻力不是恒力，其大小与深度成正比F=-f=kx，可用平均阻力来代替。

如图3-1，第一次击入深度为x1，平均阻力做功为

图3 -1

图3 -2

第二次击入深度为x1到x2，平均阻力，位移为x2-x1，做功为

两次做功相等：W1=W2。

解法二：图像法。

因为阻力F=kx，以F为纵坐标，位移x为横坐标，作出F-x图像（图3-2）。曲线所围面积的值等于F对铁钉做的功。

三、从能量的角度

1.公式W=Pt。在机车启动的过程中，如果保持发动机的功率恒定，则牵引力是个变力，求牵引力的功用W=Pt。

2.动能定理。在某些问题中，我们可由其做功的结果——动能的变化来求变力F的功：W=ΔEk。

例4：一辆汽车在平直公路上从速度v0开始加速行驶，经时间t后，前进了距离s，此时恰好达到其最大速度vmax，设此过程中发动机始终以额定功率P工作，汽车所受阻力恒为F，则在这段时间里，发动机所做的功为（ ）。

解析：解法一：在汽车启动过程中功率恒定，所以直接使用公式W=Pt；解法二：在汽车启动过程中，只有牵引力和阻力做功，合外力的功等于动能的变化，有.故BC正确。

3.功能关系法。能是物体做功的本领，功是能量转化的量度。由此，对于大小、方向都随时变化的变力F所做的功，可以通过对物理过程的分析，从能量转化多少的角度来求解。

例5：两个底面积都是S的圆筒，放在同一水平面上，桶内装水，水面高度分别为h1和h2，如图4所示，已知水的密度为ρ。现把连接两桶的阀门打开，最后两桶水面高度相等，则这过程中重力所做的功等于_____。

图4

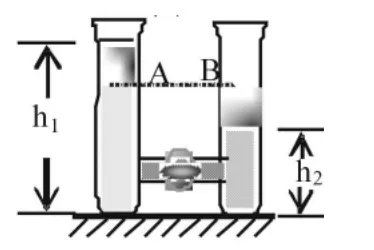
图5

分析与解：由于水是不可压缩的，把连接两桶的阀门打开到两桶水面高度相等的过程中，利用等效法把左管高以上部分的水等效地移至右管，如图5中的斜线所示，最后用功能关系，重力所做的功等于重力势能的减少量，选用AB所在的平面为零重力势能平面，则画斜线部分从左管移到右管所减少的重力势能为：

G632.0

A

1674-9324（2014）21-0085-02