谈谈错例资源在数学教学中的作用
2014-07-01张启淼
张启淼
(福建省尤溪县八字桥中学,福建 尤溪 365100)
谈谈错例资源在数学教学中的作用
张启淼
(福建省尤溪县八字桥中学,福建 尤溪 365100)
数学练习中学生出现错误是美丽的,是他们朴实思想最真实的流露。用资源的眼光看待学生学习中的错误,错误其实是学生在学习过程中创造出的一种宝贵的教学资源,是一种来源于学习活动本身,直接反映学生学习情况的生成性教学资源。结合我多年教学的实践,谈谈个人的几种看法。
教学资源;错例;求知欲
在平时的教学中,我们常常会遇到这样的现象:重要的知识点讲过多次之后学生还是会出错,大有“野火烧不尽,春风吹又生”之势。而且学生在课堂上、作业中出现的错误经常是类同的,有些错误是一犯再犯,甚至有的学生一道题目需要订正好几次才能订正好。但长期以来,对待学生学习上的错误,我们缺乏一种“主动应对”的理念和策略,导致在教学实践中经常可以看到有相当一部分学生对于相同的错误屡犯不止,学生学习时间的无效流失,影响着教学质量。
俗话说:“失败是成功之母”,错误是正确的先导,是通向成功的阶梯,是创新火花的表现,我们要懂得“变废为宝”。教师要善待学生的错误,并善于挖掘学生错误思维中的合理因素,学会欣赏错误思维中的创新因素,将错误转化为宝贵的教学资源,让错误发挥出它最大的价值和功能。下面,我根据多年的教学实践,从以下几个方面谈谈我个人的看法。
一、错例是激发学生求知欲的有效措施
错例分析具有正例示范所不可替代的作用,两者相辅相成,构成完整的解题教学。教师做好典型错例分析,寻找跟进对策是帮助学生学会学习的方法之一。教师通过错题分析或者通过师生的共同分析,找到错题的症结所在,采取相应的方法辅导、改进后,再让学生进行相应的练习,学生的正确率会有较大的提高,面对自己的学习效果,加上教师的激励性评价,学生的信心大大增强,是激发学生求知欲的有效措施。
例如,在“分式的运算”课中让学生做了这样的一道题:

请三位同学上黑板解,其中一位同学的解法是:
解:原式=2(x-2)+5(x+2)-4(x+3)=3x-6
他的解法显然错了。当教师点评到这位同学的解法时,引来了下面学生的一些嘲笑。教师问其他同学:“他这道题的解法错在哪呢?”这下,课堂气氛一下子活跃起来了,同学们七嘴八舌地说:“他把分式方程变形(去分母)搬到计算题上了,结果丢了分母。”这位同学一下子红了脸,不好意思地低下了头。这时教师对同学的说法不予置评,沉思了一会儿,干脆来个“将错就错”。“刚才这位同学把计算题当作方程来解了,虽然解法错了,但是给了我们一个启示,若能将该题去掉分母来解,其‘解法’确实简洁明快,因此,我们能否考虑利用解分式方程的解法来解它呢?”教师这么一说,刚才这位同学的头也慢慢地抬了起来。“一石激起千层浪”,其他同学也纷纷议论起来,寻找解决问题的新方法。在大家的踊跃探求下,一个新的解法也就诞生了。

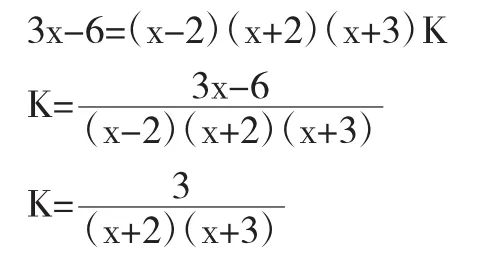
学生很开心:“我们又掌握了一种新的解法,太好了。”大家都体验到了成功的喜悦。教师接着又对这位同学作了激励性的评价:“刚才,你的解法虽然错了,但你的这种‘用方程的思想解分式计算题’的思想却是一种寻求简便的思想,是自己思维的真实展示,给了我们有益的启示。”这位同学的脸上也露出了笑容,脸上洋溢着自信。令教师没想到的是,这位同学以后上数学课都特别的认真,而且信心十足,对数学也分外的喜爱,上课更是大胆发言,对有些问题的解决也常常有自己的独到之处。
二、错例是加深理解基础知识的重要手段
学生新学一个定义、法则、公式和性质的时候,往往把其间的关键性词语忽略或对其符号意义不明而造成错误,这时的错例就成了加深理解和记忆的重要手段。
例如,在利用配方法解一元二次方程时,教师出示了以下例题:

教师让学生仔细观察后问:“以上解答过程是否正确?若不正确,请同学们找出错误原因,并做出正确解答。”在观察过程中许多不细心的学生根本看不出破绽,感到很疑惑,都产生了想得到正确答案的渴望,教师让学生思考几分钟后,叫一位学习成绩优异的学生在错例旁板出正确的解答过程:
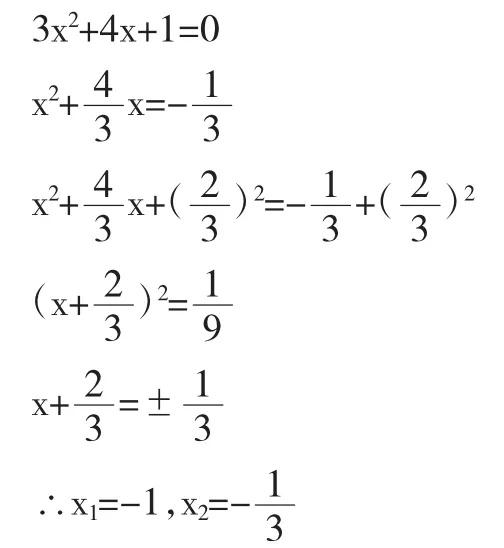
教师让学生观察、比较错例和正例,通过观察、比较不难看出,错例在解答过程中没有先将二次项系数化为1,学生因此牢牢记住了在利用配方法解一元二次方程时,应先将二次系数化为1,加深理解和掌握解题方法。
三、错例是纠正错误的常用方法
对一些学生在认识上的模糊,从正面又难以说清的问题,教师能举出一个或几个生动而击中要害的错例,引导学生讨论,往往能收到比较好的效果。
例如,在七年级学生学习数轴时,教师画了这样一条数轴:

图1
问:“这是数轴吗?”班级同学几乎异口同声大声回答:“不是数轴!”一个个显得得意的样子,这答案很明显错了,他们总认为数轴哪有这么简单,所为数轴应该要像这样(如下图):

数轴既要有负坐标又要有正坐标,他们对数轴的“三要素”理解还不够透彻,所以教师又问:“真不是吗?”他们还是回答:“不是!”教师说:“好,下面请同学们在图1中找出原点、正方向和单位长度。”通过教师帮忙,同学们很快就找出了图1中数轴的“三要素”,同时也确认了图1是数轴,并很好地掌握了关于数轴的基础知识。
往往像以上这样的问题,教师通过设置错例的方式来帮助学生巩固知识,对学生纠正答题中的错误肯定很有帮助。
四、错例是发现问题的重要途径
教师讲清了概念,学生记住了概念,并不等于真正理解和掌握了概念,还要通过计算和解题实践来加以检验。教师精心设计一些易错题让学生练习,是一个发现教学上存在问题的重要途径。
例如,在一元二次方程这一章解题中,往往学生容易忽略二次项系数a≠0及最高次数为2次的方程,所以教师可设计易错题如:若方程(m-2)x(m2-2)-4x+3=0是一元二次方程,则m满足条件:____。在教学过程中很多学生会只考虑m2-2=2,得出答案是m=±2,这时教师问:请m=2把带回方程看看,学生就会发现二次项为0,才知道m-2≠0这一条件,即二次项系数a≠0,所以本题m只能为-2,不能为2.
又如,在教学“三角形的内角和”练习中,教师在黑板上出示下面三组角:
第一组∠1=35°,∠2=75°,∠3=70°;
第二组∠1=15°,∠2=25°,∠3=60°;
第三组∠1=100°,∠2=65°,∠3=90°。
要求学生分别做出这三个三角形。片刻之后,学生做成了第一个三角形。但按第二组和第三组的条件,无论如何也不能做成三角形。学生顿生疑团,议论纷纷,不知所措,急需求教于教师。这时,教师让学生分别画一个直角三角形、锐角三角形和钝角三角形,量一量它们的三个角,看一看三角形内角和有什么规律。这样,通过测量、验证,学生恍然大悟,原来三角形的内角和是180°,而二、三组两个三角形的内角和不等于180°,所以无法做出这两个三角形。
利用错误拓展师生共同成长的空间,使课堂中的错误成为一种重要的课程资源,这是新课程改革背景下教师促进学生学习、达成教学目标的必由之路。当我们以满腔的热情,严谨的态度,科学的方法来对待、亲近它时,它将给我们呈现教学的革新。
G632.0
A
1674-9324(2014)21-0084-02
