超声振动切削温度场的建模及试验研究

2014-07-01王国力郑菲菲李媛

河南科技 2014年4期

关键词：切削速度热源温度场

王国力郑菲菲李媛

(1.卡特彼勒（郑州）有限公司，河南郑州 450103；2.济源华新石油机械有限公司，河南济源 454650；3.河南机电高等专科学校机械工程系，河南新乡 453002）

超声振动切削温度场的建模及试验研究

王国力1郑菲菲2李媛3

(1.卡特彼勒（郑州）有限公司，河南郑州 450103；2.济源华新石油机械有限公司，河南济源 454650；3.河南机电高等专科学校机械工程系，河南新乡 453002）

本文针对超声振动切削温度场进行了计算和分析研究，从解析法入手，建立了关于超声切削温度场的传热学模型；并根据现场情况和试验条件，简化处理了该模型，最终求得了一个符合实际加工要求的超声切削传热学模型；根据试验条件确定了模型中的参数值，并进行了理论公式计算结果和试验结果的对比，验证了该模型的正确性。

超声振动；温度场；理论计算；试验研究

1 引言

切削热和因此产生的切削温度是切削过程中存在的重要现象，它是分析刀具磨损、破损和加工质量的重要因素。刀具体内的热应力分布直接受切削温度的影响，特别是在超声切削的过程中，刀具将会受到周期性的热冲击，这将使得硬质合金刀具产生热裂纹进而导致破损[1]。因而，对温度场进行分析研究是十分必要的，在这里我们运用热源温度场迭加法建立了超声切削过程中工件表面的温度场，其原理是运用固体导热微分方程的热源解，经过迭加从而求解出复杂温度场的传热学模型[2，3]，该方法尤其适用于分析计算各种热源状态的非稳态温度场。

2 超声振动切削温度场建模

刚切入工件时，刀具产生的热量小，因而它的热强度小，当快切出时，刀具的热强度最大，而切出后刀具的热强度为零，因此热源密度可以按照三角形分布的情况来进行考虑，如图2所示。三角形分布的热源密度公式为[4]：

T1——切削周期，η——切入工件的时间与切削周期T1之比。

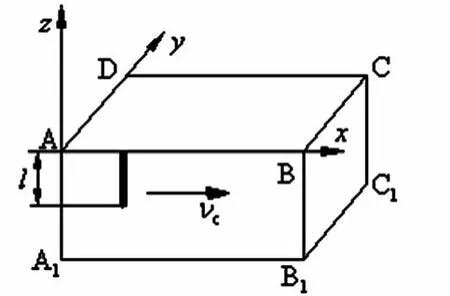
图1 热源移动模型

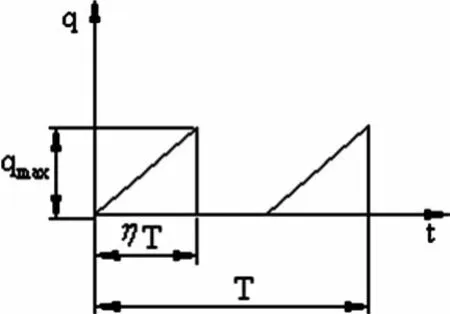
图2 热源密度分布

此处求的是以速度Vc沿轴向移动的线热源，经过一段时间t以后工件上任意一点M（x，y，z）处的温升。可以采用微元法将整个时间段t分解成无数个微小的时间段dti，并且取其中在ti时刻的一个微小时间段dti来进行分析。在dti瞬间该运动着的线热源所发热量为q(ti)dti，从该时刻到观察时刻的时间间隔为τ，τ=t-ti，这时热源离观察点的距离为：x轴方向的距离为（xυcti），y轴方向的距离仍是y。由此就可以把微小时间段dti内的线热源视作瞬时有限长线热源。在此依据文献[4]的瞬时有限长线热源的温度场公式并且考虑到镜像热源有：

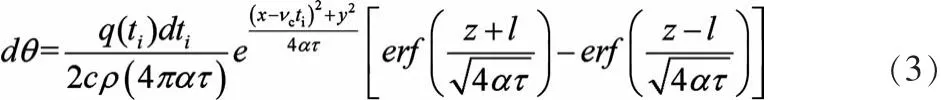
将三角分布的热源密度公式（6）带入上式后两边积分得：

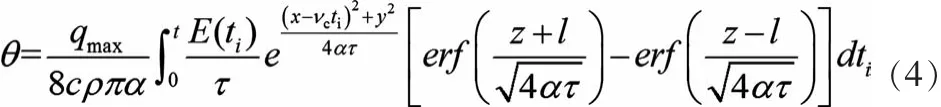
由于为热源开始时刻到观察时刻的时间，所以τ=t-ti，则dτ=-dti，当ti=0时τ=t，当ti=t时τ=0。带入上式得：

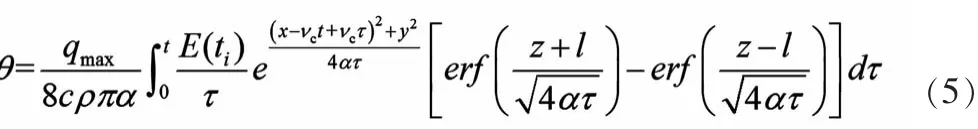
线热源强度可用如下公式计算，根据切削用量知，

式中：v为切削速度，cm/s；Fz为切削力，g；J为热功当量g· cm/cal；l为线热源的长度；β1为热量传入工件的传热比。

再来考虑一下镜像热源，因为对移动平面镜像过后的镜像热源同其原热源是完全一致的，因此将式（5）的结果改成两倍就行了。最后就可以得出关于工件表面温度场的一个解析公式：

第二，提升成人网络学习特质。当成人学习者特质与网络媒体特性交互作用时，会影响学习结果。尽管基于ICT的成人学习者会有不同的学习倾向，但是，成人学习者具有的自我导向学习倾向、批判反思性品质，以及善于合作、互动、应用、建构知识等学习特质，都有助于成功的成人学习。学习者必须于网络环境中学习如何学习，在学习ICT有关知识的同时，更需要思考如何利用ICT进行学习。只有提升这些学习品质，学习者才会依据自身的需要，主动制定学习目标，寻找学习资源，执行学习策略以致评估学习成果。

工件表面温度场就能使用公式（7）来计算了，从公式（7）中容易看出，工件表面上的温度与很多的因数都有关，它不仅仅与热源的作用位置和时间有关，还与切削力、工件的材料特性、切削速度等有关系。

3 超声振动切削温度的理论计算及试验研究

3.1 根据试验条件简化温度场解析式

在本文中是使用自然热电偶的方法来测量切削区平均温度的，相应的试验条件为：超声波功率为P=70W，振幅为A= 13μm，频率为f=19.39KHz；试验所使用的刀具为YG6刀具，该刀具的主偏角kr=75°；切削条件为干切；切削参数以切削深度αp= 0.1mm，切削速度v=27.5m/min，进给量f=0.043mm/r为基础试验参数，从而能计算出切削宽度aw=0.104mm；工件材料为SiCp/Al，其密度ρ=2.76g/cm3、导热率λ=174w/（200℃）、比热容c=883J/ （kg·℃）；热源的移动速度vc=v/K，K为切屑收缩系数，一般切削情况下，K=1.7～2.2，本文中取K=2.0，可计算得vc=13.75m/min。

试验测的是切削区的平均温度，计算过程中的观察点也就是切削点的位置，那么的坐标为（0,0,0），将其带入公式（7）得：

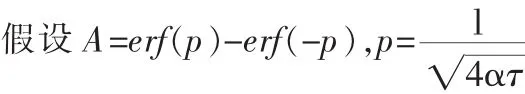
由于误差函数是一个奇函数，所以A=2erf（p）。热源长度l等于切削深度0.01mm，导热介质的导温系数α=λ/（c·ρ），带入数值得α=71.47mm2/s。因为观察点就是切削点，也就是线热源所在点，所以τ→0，则p→∞，此时的erf（p）→1，在此情况下可近似看成erf（p）≈1，则A=2，那么公式（8）又可简化为：

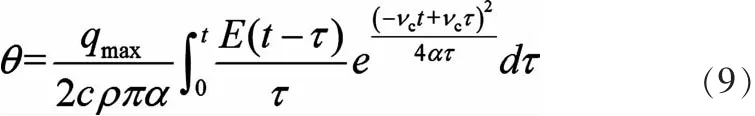
3.2 解析式中参数值的确定

式（9）中的部分参数可以通过计算和试验得出，式中的切削周期T=1/f=5×10-5s，η为切入工件的时间与切削周期T的比值。在超声切削过程中则是一个周期的净切削时间Tc与周期T之比，由计算得：

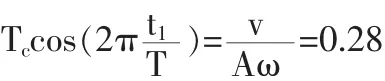
由文献[5]表3.1可查得，η=0.33。

传热比β1是一个难以确定的参数。不同的加工材料，不同的加工参数，不同的刀具对传热比都有影响的。此处我们通过计算与试验结果来反求传热比β1。超声切削的试验结果与求的β1值如表1所示。试验参数为：f=0.03mm/r，0.043mm/r，0.064mm/r，n=125r/min，αp=0.1mm，试验条件见《超声振动辅助车削PRMMCs的温度试验研究》论文，切削SiCp/Al平稳后取其温度的平均值。

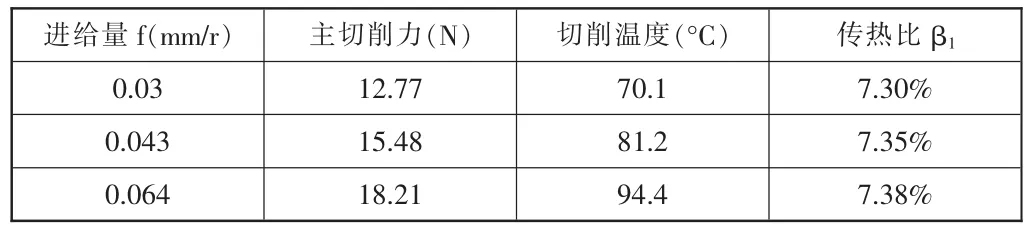
表1 试验结果与的计算结果表

从表1容易看出，进给量对热量传入工件的传热比的影响是很小的。对表1中传热比的值求平均后作为理论计算的传热比β1，即β1=7.34%。

3.3 理论结果与试验数据的对比

为了验证推导出的超声切削的温度理论模型，依据理论计算公式针对不同切削速度条件下的切削温度进行计算，与得出的试验数据对比从而来判定温度理论模型正确与否。理论计算及试验参数为：进给量f=0.043mm/r，切削深度αp=0.1mm，改变工件转速n=90r/min、125r/min、180r/min、250r/min，干切削，YG6刀具，工件材料为SiCP/Al复合材料。

图3 超声切削温度的理论计算值与试验结果

试验数据结果和计算结果图3所示。由图可知，试验结果与计算值之间有一定的偏差，但是偏差不大，最大的偏差不超过8°C。在误差允许的范围之内，说明计算结果与试验结果还是比较吻合的。

从图3还可以看出，在n=125r/min时计算值与试验结果的偏差最小。这是因为在计算传热比β1时是以其为基本参数的，切削速度变化时，传热比β1也发生变化，但是在计算时把它看作了一个定值。如果考虑传热比β1的影响，在切削速度低于125r/min时，传热比要比7.34%大，在高于125r/min时，传热比要比7.34%小，那么计算值在低于125r/min时就应该比图中的计算值大，而在高于125r/min时就应该比图中的计算值小，这样计算结果会更趋近试验值。

试验结果与理论计算值之间有一定偏差的原因还有以下两点[4]：

（1）在建模时，转换了切削的工况条件；在推导解析式的时候，对切削过程进行了理想化、简单化了。比如在建模时，把工件视作无限大的平面，而实际上工件是有一定体积的；在切削过程中，工件、刀具和空气之间存在着对流热交换，虽然不大，但却把这个热交换忽略为零了。

（2）由最终的理论公式容易看出，它是需要以一定的试验结果为输入量的，比如切削力是由试验测量得出的，传热比β1是由实验结果逆推出来的，这些都会使得理论计算结果产生一定的误差。