江河水质模型预测初探
2014-07-01刘建国刘建华郭洪光
刘建国,刘建华,郭洪光
(1.长春师范大学传媒学院,吉林长春 130032;2.吉林省环境研究院,吉林长春 130000)
江河水质模型预测初探
刘建国1,刘建华2,郭洪光2
(1.长春师范大学传媒学院,吉林长春 130032;2.吉林省环境研究院,吉林长春 130000)
本文以某江为例,针对江河水质的污染状况,对实测所提供的数据进行研究与分析,建立一个完全混合水质系统数学模型,利用目标函数求解,采用灰色理论中的相关参数估计法预测江河干流水质的情况。
水质模型;完全混合水质系统;灰色系统;预测
1 某江及其沿线地区的水质评价
对某江近两年来水质情况进行定量综合评价.其中,监测值的精确性和统计方法的合理性是决定评价精度的重要因素.
1.1 评价参数
一般来说,评价河流的参数包括水质参数、氧平衡参数、重金属参数、有机污染物参数、无机污染物参数以及生物参数.而某江河流以DO(氧)、CODMN(无)、NH3-N(无)污染为主,pH值(水)对某江水质影响不大,一般情况都保持在(6~9)酸碱平衡状态.
1.2 超标倍数
定义1 超标倍数:测试值和目标准限值的差值与准限值的比值.公式记作k=|c0-c|/c,其中,c0为测试数值,c为目标准限值.
根据表1提供的数据进行统计,观测期BOD最大值达11.0,DO最大值可达12.69.
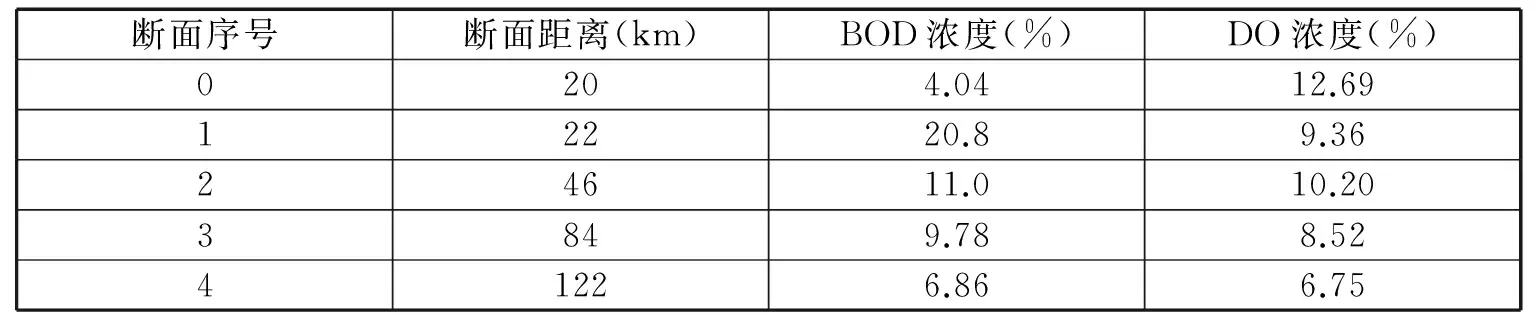
表1 某江各时期水质类别统计表
1.3 某江年度水质变化分析
按观测期统计各时期水质类别百分比,研究某江水质变化情况.第一、第二江段k值实际计算结果如表2所示.
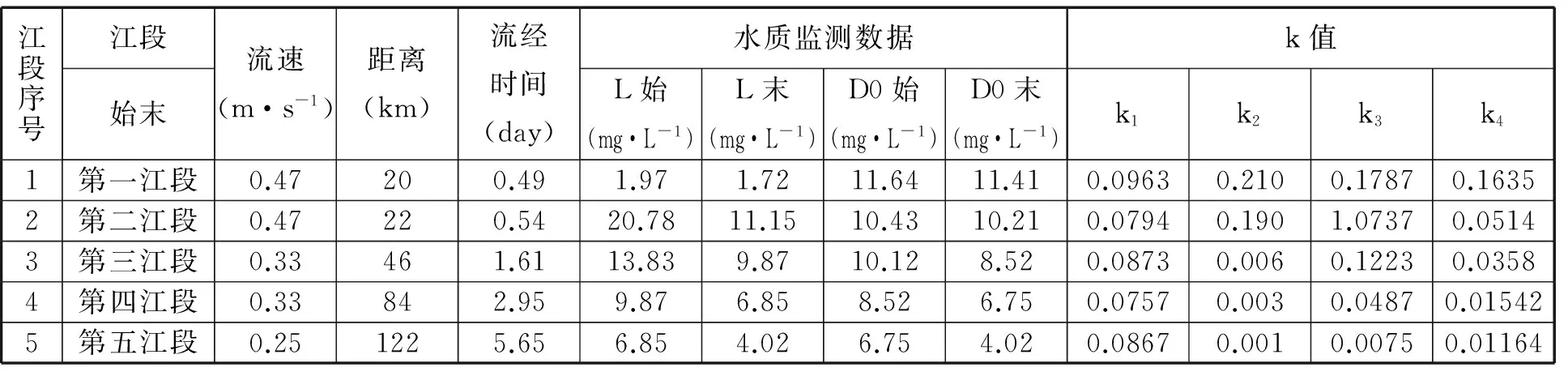
表2 某江第一、第二河口水质参数计算结果
注: (1)江段1计算结果k值使用范围(13km);(2)江段5计算结果k值使用范围(第5江段)。
由表2可以看出,每个江段k1值波动不大,在0.096~0.075之间波动.其主要原因是参数k1值波动受江水温度和主要污水成份含量的影响.冬季,某江的第一、第二河口江段,受其上游泄排热水的影响,部分水域水温高于总体均值;其余各部分江段常年水温均控制在1℃~0℃间.主要污水成分含量对k1值的影响,呈现在最严重的第二断面污染较明显.第三河口和第四河口因为没有主要污染成份的江水排入,所以其污染主要成份多无变化,主要参数k1值变化不大.
以第二江段为界参数k2值,分为两个阶段.上游江段的 k2值在0.220~0.190之间;下游江段主要参数k2值骤然下降至0.006~0.001之间,其主要原因是k2属温度和流动状态的双重函数.第三江段因上游来水受水坝阻断和热污染的影响,冬季江水不封冻,复氧条件较好,主要参数k2值较高.该江段江水溶解氧高于10mj·L-1.而下游江段江水冬季封冻,复氧条件极不利,主要参数k2值骤降.关于封冻状况下复氧速率的研究国内外鲜见报导.我们参考国外的研究,提出某江冬季冰封江水参数k2值低于0.033/日.
参数k3值主要源于悬浮物颗粒的构成和河流水纹条件,污水中BOD存在形态主要为悬浮物、胶体粒子和水溶性物质三类.BOD在河水中的衰减主要原因(大于80%)是沉积作用.在第三江段,BOD中的悬浮物含量较少,k3值为0.178;在第四江段,BOD中的大量悬浮物排入江中,水流沉积较快致使该江段k3值迅速增至1.095;第二江段以下部分,江水流速枯水期值均在0.4~0.2M·S-1之间,悬浮物沉降条件有利,前江段悬浮性BOD沉降较多,故k3值迅速降低,依次降为0.122、0.049、0.008,降幅明显.同时随着汛期重新到来,BOD中的悬浮物会泛起(再悬浮)并继续向下游输运,再次对水体的耗氧过程产生影响.本研究不对此进行讨论.
2 建立完全混合水质系统的数学模型分析污染源的分布
2.1 完全混合水质系统的数学模型的建立
根据水文动力学模型,运用物质守恒原理,描述水体中污染物随时间和空间迁移转化的规律,建立稳定的水质模型.假设降解系数K=0.2不变,对主要污染物BOD和DO在某江干流中的浓度值(主要受水流量Q与水流速v的影响)进行分析.在一个完全混合的水质系统中,假定系统的所有参数不随时间变化,物质平衡可描述为一个微分方程.
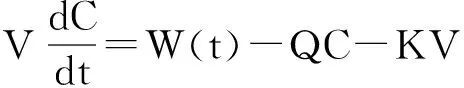
(2.1)
其中,V-容积(L3);W-排污物(M/T);C-产生浓度(M/L3),C按一级反应分解;Q-通过系统的流量为 (L3/T);K-衰变系数为 (T-1).
边界条件为T=0时,C=C0.
上式方程的解为C(t)=W/(Q+KV)*(1-exp(-(Q/V+K)t)).
在稳定状态下,有
C=W/(Q+K*V).
(2.2)
(2.2)式即为完全混合水质系统下的数学模型.
2.2 计算机程序求解目标函数最值
完全混合水质系统下的数学模型为C=W/(Q+K*V),设W设置为常量,横截面积为S,长度为L,流速为v,则
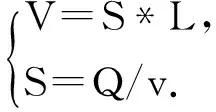
(2.3)
从而推出
C=W/(Q(1+KL/v).
(2.4)
当W为恒量时,浓度与Q(1+KL/v)成反比(K=0.2/天).用C语言二维矩阵求解上式,并用冒泡法对均值排序.
设矩阵
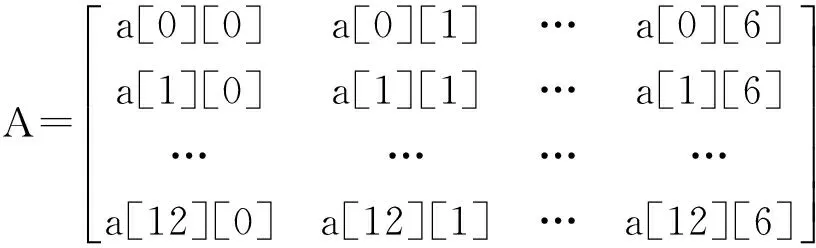
程序段如下:
Main()
{int i,j;
float Q,L,v,x,temp;
float a[12][6],c[12][6],K=0.2;
/*置入初值*/
for (i=0;i<=12; i++)
for(j=0; j<=6; j++)
a[i][j]=0; }
/*输入数据*/
for(i=0; i<=12; i++)
for(j=0; j<=6 ;j++)
{printf(“Please input the parameters!Volumn Q,length L,speed of flowing”/n);
scanf(“%f,%f,%f/n”,&Q,&L,&v);}
for(i=0; i<=12 ;i++)
for(j=0; j<=6; j++)
{{m=K*L;n=m/v;
c[i][j]=Q*n;
printf(“%f,c[i][j]”)}
printf(“/n”);}
/*计算各观测点全年浓度均值*/
X=0;
for(j=0; j<=6; j++)
{for(i=0; i<=12; i++)
X=x+c[i][j];
d[j]=x/13;
printf(%f,d[j]);}
/*用冒泡法排序*/
i=0; j=0;
for (i=0; i<=5; i++)
for(j=i+1;j<=6;j++)
if(d[i]>d[j])
{temp=d[i];
d[i]=d[j];
d[j]=temp;}
for(i=0;i<=6;i++)
printf(“%d”,d[i]);}
3 进行基于灰色系统的某江水质预测
3.1 灰色系统的引入
数列预测是对某现象随时间的顺延而发生的变化所作的预测.灰色系统的预测一般分为数列预测、灾变预测、系统预测和拓扑预测4种类型.某江的年平均流水量为34674.47亿立方米,由于全流域内干支流分布复杂,河段水质在枯水期与丰水期呈现较大差异.根据某江流域近10年水质报告中所显示的现象,水质数值在不同年份呈现随机的、有序的、有界的状态.因此,可以就某江废水排放量建立灰色预测模型,对某江年废水排放总量进行预测.
3.1.1 GM(1,1)模型
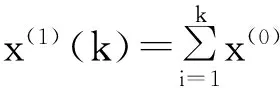
(3.1)
采用累加法生成新时间序列,以弱化原始序列的随机性和波动性.
(3.1)式中,x(0)为原始时间数列,由x(0)(1),x(0)(2),…,x(0)(n)组成;x(1)为累加时间数列,由x(1)(1),x(1)(2),…,x(1)(n)组成.
GM(1,1)模型为一阶微分方程:
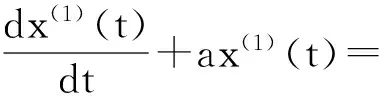
(3.2)
方程x(1)(t)为x(0)(t)的依次累加值,即系统的逐年累计总量;而方程左边第一项为系统的逐年增量,即系统的发展速度.求微分方程的解,可得到时间函数.
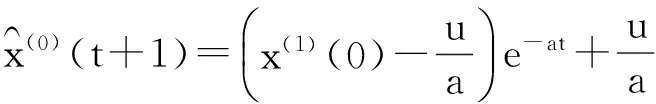
(3.3)
再累减还原,得到
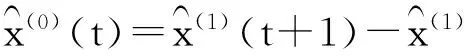
这两个方程即为模型时灰色预测的基本计算公式.
3.1.2 估计参数方法
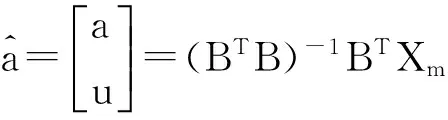
3.2 建立灰色预测模型
3.2.1 给出累加时间数列预测模型
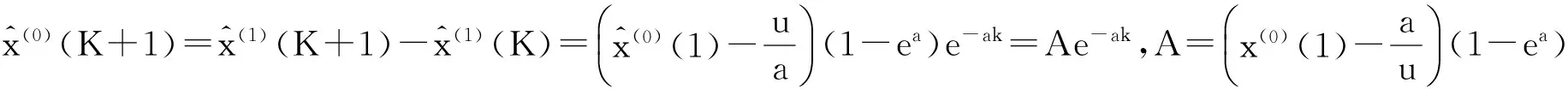
3.2.2 原始数列预测模型
对累加时间数列预测模型进行累减,得到

(3.4)
其中,K=1,2,3,…
3.3 江水排量的计算与预测
3.3.1 计算
以某流域2000-2010年废水排放量作为原始序列建立GM(1,1)模型,求得
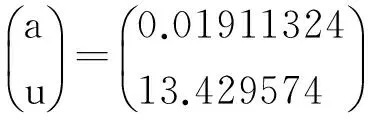
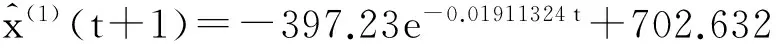
3.3.2 检验
构造方差比和小误差概率,对模型作检验
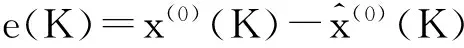
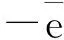
由灰色模型认为,通过检验的标准为精度等级越小越好,四级为不通过.精度等级表如表3所示.

表3 GM(1,1)模型等级
根据拟合数据,对模型精度进行检验计算,测得方差比值C=0.47,小误差概率P=0.91,两项检验指标都通过,精度等级为二级;曲线拟合度好,模型精度较高,灰色预测成功.
[1]程声通,陈毓龄.环境系统分析教程[M].北京:高等教育出版社,2000:59-63.
[2]傅国伟.河流水质数学模型及其模拟计算[M].北京:中国环境科学出版社,1985.
[3]谢永明.环境水质模型概论[M].北京:中国环境科学出版社,1996.
[4]廖振良,宋卫锋.应用水质模型方法研究河流污染控制[J].环境与开发,2010(15):15-16.
[5]中国环境影响评价[Z].北京:化学工业出版社,2013(2)36-38,(5)174.
[6]国家环境保护总局.2012年中国环境状况公报[J].环境保护,2013(7):3-13.
2014-08-11
刘建国(1972- ),男,吉林长春人,长春师范大学传媒学院副教授,从事计算数学与信息技术教学研究。
X52;O29
A
2095-7602(2014)06-0004-05
