“逐差法”在高中物理实验中的应用值得商榷

2014-06-29邹会坤

物理通报 2014年4期

关键词：钩码差法间隔

邹会坤

（山东英才学院山东济南 2501 04 ）

逐差法是针对自变量等量变化，因变量也做等量变化时，所测得的有序数据等间隔相减后，取其逐差平均值得到数据的方法．逐差法的优点是充分利用了测量数据，具有对数据取平均的效果，减小了随机误差的影响．它是物理实验中处理数据常用的一种方法．

逐差法有其具体使用条件，但如果没能从实验的实际出发，一味地使用逐差法处理数据以减小随机误差，有时可能只是做了表面文章，得不到减小误差的效果．在高中教材“匀变速直线运动的实验探究”的实验中，利用逐差法求加速度就有不妥之嫌，现分析如下．

1 逐差法分析纸带求加速度的初衷

如图1所示为研究匀变速直线运动时打点计时器所打出的一条纸带，图中的0，1，2，3，4，5，6为计数点，相邻计数点间的时间间隔为T，所测的相邻计数点间的位移分别为x1，x2，…，x6．

图1

由Δx＝a T2求得加速度

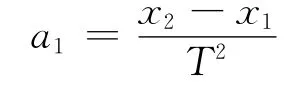
再取它们的平均值

从式（1）可以看出，在计算平均值的过程中，中间数值x2，x3，x4，x5都被消去，只利用了首尾两个数据x1，x6，显然不能利用多个数据减小随机误差．因此，教材和教参中就提出了隔项逐差法．

将连续的数据（必须是偶数个）x1，x2，…，x6从中间对半分成两组，再利用间隔相减求加速度

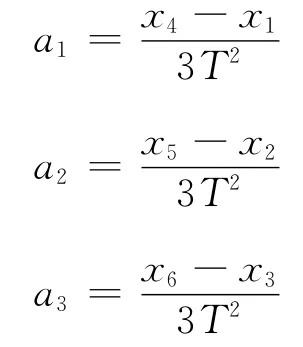
然后求平均

从式（2）可以看出，隔项逐差法利用了全部数据，减小了测量造成的随机误差．

2 逐差法分析纸带求加速度的缺陷

前面逐差法求加速度的初衷分析看似天衣无缝，但从减小实验误差的实际操作分析，就会发现有很多不妥之处．

从测量角度来看，这种分段测量连续相等时间通过的位移的方法不利于减小随机误差，因为在用刻度尺测量操作时，往往需要多次移动刻度尺的位置，读数带来的随机误差不仅与末端的读数估计有关，还与起始端是否与某刻线对齐的估计有关，这样，会导致更大随机误差的产生，而且操作也不方便．另外，在相同条件下，用同一把刻度尺测量长度时，被测量的长度越长，其相对误差会越小，分段测量多段较小长度，相对误差会更大．因此，在实际实验操作时，一般采用固定刻度尺直接读取每个计数点的位置坐标的方法，然后，再利用位置坐标计算所需的位移，这样，刻度尺某刻线是否与起始点对齐产生的零误差就会完全相互抵消了．这也是目前多数考题中提供实验数据的方式．

图2

如图2所示，在图2提供的原始数据条件下，计算出连续相等时间的位移

x1＝s1

x2＝s2－s1

x3＝s3－s2

x4＝s4－s3

x5＝s5－s4

x6＝s6－s5

然后把它们代入到逐差法得到的式（2）中得

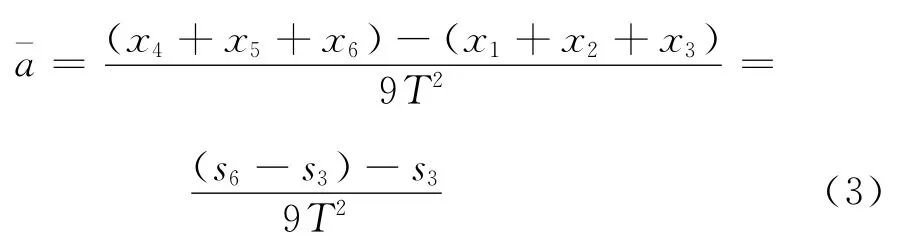
由式（3）结果来看，利用前面的逐差法，经过比较复杂的计算，最后却只用了s3，s6两个数据，而且相当于只是利用了两段连续相等的位移（s6－s3）和s3的差求得了加速度，这又何谈提高数据利用率，减小随机误差呢？显然，这与逐差法最初的设计思想相悖．

鉴于前述，该实验利用Δx＝a T2求加速度的方法颇为简单，如图3所示．

图3

选择间隔较远的3个计数点0，1，2（相邻计数点间的时间间隔为T），采用刻度尺定位法测量1，2点分别到0点的距离，而且每个距离利用多次测量求平均的方法，最后，用两段连续相等时间间隔的位移差计算加速度，即

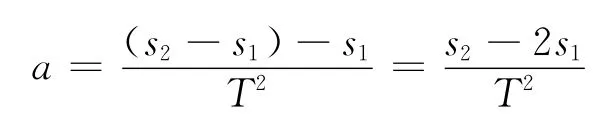
显然，与“逐差法”相比，这种测量和计算及对原理的理解都大大简化了，所以可得出结论，即在“匀变速直线运动的实验探究”实验中，由于“逐差法”的引入，使本该容易理解的原理变得复杂，使容易进行的测量和计算变得繁琐，不仅没有减小测量随机误差，反而增大了测量随机误差．同时也导致大量不切实际考题的出现，误导了大批学生和教师．