玻尔兹曼因子等温线对气液相变与临界系数的数学描述

2014-06-29吴义彬

物理通报 2014年6期

吴义彬

（南昌市老科学技术工作者协会江西南昌 3300 03 ）

1 引言

“热力学的统计理论（即微观的）基础的发展是19 世纪物理学的卓绝成就之一．虽然，这个发展的许多观念都源出于麦克斯韦和玻尔兹曼，但正是吉布斯的工作更直接地影响着现代对平衡态统计力学的表述．近70 年来，我们对相变和临界现象的理解与进展，本质上，体现在吉布斯表述在各种各样的物理问题中的应用．其中有些直接紧密地联系着实验的事实，其他则表现为一些理想问题，它们用萃取理解各物理现象特征的观点表达出来．如果用单个简洁的结论能概括70 年以来这个领域的发展，那就是平衡态热力学的统计理论基础取得的辉煌胜利．”［1］杨振宁先生殷切期望的“单个简洁的结论”，至今仍是人们梦寐以求、不懈奋斗的目标．

与“吉布斯表述”方法不同，直接从玻尔兹曼观念出发，在平衡体系边界区域的表面保守力场中应用玻尔兹曼分布律，导出分别描述气体与液体的玻尔兹曼因子方程，不仅可以对液气相变过程中的相变潜热［2］（气化热与沸点气化熵）、液体表面张力系数及其温度变化率［3］等在定量上进行准确的数值计算，而且还可以得到与安德鲁斯实验实测等温线［4］完全一致的玻尔兹曼因子等温线．真正实现了用简洁的数学语言在定量上准确描述气液相变和临界系数的目标．

2 玻尔兹曼因子等温线

图1是1869 年安德鲁斯仔细地对C O2气体的等温压缩做了实验后而得出的几条实验等温线［4］．

图1 C O2实验实测的等温线

图1所示的p－Vm图（图中的横坐标为摩尔体积Vm）表明：

（1）当温度低于临界温度Tc时，该二氧化碳实际气体的等温线有气液相变的直线段，随着温度的升高，相变过程的直线段逐渐缩短．

（2）当温度增加到临界温度Tc时，饱和液体与饱和气体之间的界限已完全消失，呈现出模糊状态，称为临界状态．二氧化碳的临界压力pc为72 ．3 a t m，临界温度Tc为31 ．1℃．在p－Vm图上，临界温度等温线在临界点上是拐点．临界温度以上的等温线也具有拐点．

（3）当温度在48 ．1℃以上时，等温线才成为相对较为均匀的曲线．

图2 C O2玻尔兹曼因子等温线

图2是在反思范德瓦尔斯等温线“公认缺陷”的基础上，采用气体的玻尔兹曼因子方程［5］和液体的玻尔兹曼因子方程［3］共同描述等温压缩二氧化碳全过程的玻尔兹曼因子等温线．其中，气体的玻尔兹曼因子方程式为

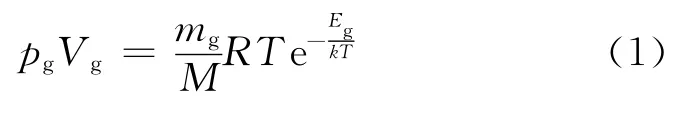
或

式中mg为气体质量；pg为气体的压强；Vg为质量为mg的气体体积；Vgm为气体摩尔体积；M 为气体摩尔质量；Eg是紧靠容器壁的气体分子所具有的表面自由能，数值上等于体系内部一个分子通过表面保守力场溢出体系（节流）过程中所必须做的功．液体的玻尔兹曼因子方程为

或

式中pg为饱和蒸气压；Vi为质量为mi的单元液体的体积；Vim为液体摩尔体积；M 为摩尔质量；Ei为液体表面自由能，数值上等于液体内部一个分子穿越液气界面区域转化为蒸气分子过程中必须克服界面保守力场作用所做的功．

与图1相对照，图2除新增了A1，A2，A3，a1，a2，a3，o1，o2，o3，b2，b3等拐点标识之外，与图1完全一致．换言之，玻尔兹曼因子等温线可以逐点对应地描述等温压缩C O2的全过程，特别是，在低于临界温度时，可以如实地描述从气体体系到气体与液体共存的非均匀体系，再到液体体系的等温压缩全过程．

3 玻尔兹曼因子等温线的数学描述

3．1 表面自由能与分子间合力曲线的对应关系

图3［4］所示的体系内部两相邻分子之间相互作用力的合力，完全对应地决定了体系边界区域表面保守力场中表面自由能Eg与Ei的有无、正负与大小［5，6］．

（1）如图3所示，当气体内部两相邻分子之间的间距r趋近于∞时，体系内部分子间将处于完全没有任何作用力的理想状态，边界区域界面保守力场将不存在，故此时Eg＝0．

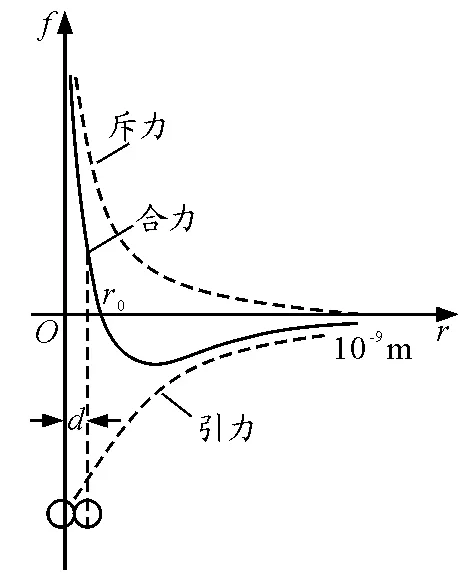
图3 分子力示意图

（2）当气体（或液体）内部两相邻分子之间处于相互吸引状态（F合力＜0）时，边界区域表面保守力场就会表现为引力势场状态，故此时表面自由能Eg（或Ei）＞0，且其大小随着图3中r0～∞区段内合力曲线的变化而对应变化．

（3）当气体（或液体）内部两相邻分子之间的吸引力与排斥力正好处于相互抵消（也即是r等于r0，合力等于零）的平衡点状态时，边界区域表面保守力场区域也将不存在（瞬态），故此时的表面自由能Eg（或Ei）＝0，是吸引力与排斥力相互抵消瞬间的（平衡点）状态参量．

（4）当气体（或液体）内部两相邻分子之间处于相互排斥状态（也即是r＜r0，F合力＞0）时，边界区域表面保守力场表现为斥力势场状态，故此时表面自由能Eg（或Ei）＜0，其绝对值的大小随着图3中小于r0区段内合力曲线的变化而对应变化．

所以，体系边界区域表面保守力场中的表面自由能Eg与Ei的有无、正负与大小，是随着图3中合力曲线的变化而对应变化的，且正、负号相反．

3．2 临界温度（含临界温度）以上C O2实验实测等温线的数学描述

（1）r＝∞（见图3）时的数学描述

由于C O2气体的体积Vg足够大（pg足够小）或温度足够高时，体系内部分子间的间距r≈∞时，分子之间的相互作用力可以忽略不计，气体体系的表面自由能Eg≈0，玻尔兹曼因子＝1．故描述摩尔C O2气体体系的玻尔兹曼因子方程式（2）［6］变为

与理想气体物态方程完全相同．所以

故此时的摩尔C O2等温压缩线为双曲线，与理想气体的等温压缩线完全相同．

解析表明，在C O2气体的体积Vg足够大（pg足够小）或温度足够高时，气体的玻尔兹曼因子方程与理想气体物态方程相同，摩尔C O2等温压缩线为双曲线，如图2中48 ．1℃以上的C O2实验实测等温线和临界温度等温线上的A2a2线段所示意．

（2）合力由零（r≈ ∞ 处）逐步递减至最小值区段内的数学描述

随着等温压缩过程，C O2气体的体积从“足够大（r≈∞处）”不断减小，相邻分子的平均间距r也就不断减小；两相邻分子间相互作用的合力（F合＜0表示为引力）也就随之逐步递减，直至最小值；表面自由能Eg（＞0）也就对应地递增，直至最大值．此时，描述C O2摩尔气体体系的玻尔兹曼因子方程式（2）变为

因为 Eg＞0

这也就是说，在表面自由能Eg随着Vgm的减小而逐步增大至最大值的过程中，图2中的a3o3，a2o2，a1o1等温线段会随着Eg的增大而越来越向Vm轴方向偏离由式（6）所描述的理想气体双曲线．a3o3，a2o2，a1o1线段还清楚地表明，温度越低，气体体系的表面自由能Eg就越大，玻尔兹曼因子就越小，式（8）右边的也就越小于式（6）中的，等温线也就越向下偏向Vm轴，越背离理想气体双曲线．直至合力（F合＜0）递减至最小值时，表面自由能Eg（Eg＞0）也对应递增至最大值，式（8）右边的取最小值，对应的点o3，o2是等温线向下偏向Vm轴的终止点，也就是等温线由向下偏向Vm轴转变为向上偏离Vm轴的拐点．在临界温度等温线上，o2点与临界点K点相重合．

解析表明，应用气体的玻尔兹曼因子方程可以逐点对应地定量描述图2中C O2实验实测等温线段a3o3，a2o2，a1o1偏离双曲线，偏向Vm轴方向的变化规律．

（3）合力（F合＜0）由最小值逐步递增至零（r＝r0处）区段内的C O2实验实测等温线

如图2所示，在o3或o2点之后进一步压缩，相邻分子的平均间距进一步减小，直至r＝r0的过程中，相邻分子相互作用的合力（F合＜0）将从最小值逐渐递增，直至等于零；表面自由能Eg（Eg＞0）也就随着合力的递增而从最大值对应地变小，直至等于零；故在此区段内，玻尔兹曼因子随着Eg趋近于零而趋近于1，式（7）也就越来越接近于式（5），等温线也就越来越向上偏离Vm轴，越来越接近于式（5）所描述的理想气体等温线．直到r＝r0（见图3）时，分子间的引力与斥力正好互相抵消，合力为零，表面自由能Eg＝0，玻尔兹曼因子，）＝1式（7也就变得与描述理想气体等温线的式（5）完全一致．故此时的等温线与理想气体的等温线相交于b点．如图2中C O2实验实测等温线上的o3b3，o2b2所示意．

解析表明，应用气体的玻尔兹曼因子方程可以在定量上精确描述图2中C O2实验实测等温线段o3b3，o2b2偏离Vm轴方向，直至与式（5）所描述的双曲线相交于b点的变化规律．

（4）在r＜r0（见图3）区段内的C O2实验实测等温线

在r＜r0区段内（即b点之后的）进一步等温压缩过程中，由于分子间的斥力与引力的不对称特性，两相邻分子之间的相互作用的合力将进入强大的斥力区段（见图3），表面保守力场将随之对应由引力势场转变为强大的斥力势场，表面自由能Eg也就会由等于零转变为小于零，且随着Vgm的减小，r的相应减小，合力（F合＞0）的急剧递增，趋向＋∞；Eg（Eg＜0）也就急剧递减，趋向－∞．故描述C O2摩尔气体体系的玻尔兹曼因子方程式（2）变为

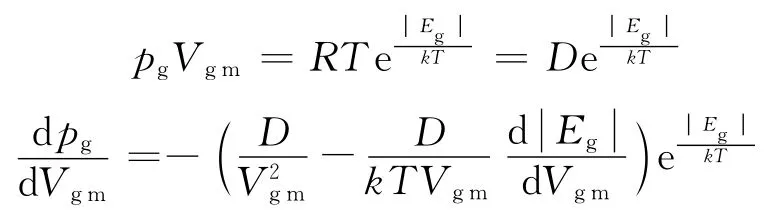
故此，在b3或b2点之后继续压缩的过程中，等温线的斜率随着V的减小迅速趋向于－∞．gm等温线脱离与理想气体双曲线相交的点b，直至与p轴近似平行．如图2中几条b3D，b2D所示意．这也就是说，气体变得越来越不可压缩．

解析表明，应用气体的玻尔兹曼因子方程可以在定量上精确地描述图2中C O2实验实测等温线段b3D，b2D的变化规律．

3．3 临界温度以下C O2实验实测等温线的数学描述

（1）饱和点之前的数学描述

由于达到饱和点之前的C O2气体体系仍遵守摩尔气体的玻尔兹曼因子方程式（2）所以，等温压缩过程与3．2节的分析类同，等温压缩线如图2中的A B，A1a1所示，当r→∞时，Eg≈0，

，

）≈1等温线近似为式（6所描述的理想气体双曲线；当Vgm减小，r随之减小的过程中，Eg＞0，且随着Vgm的减小而递增，等温线也就越来越向下偏离理想气体的双曲线，如图2中的a1o1所示．必须指出，当温度较低时，B点所对应的饱和蒸气仍可以近似为理想气体，Eg≈0，则图2中的A B线段仍可近似认为与理想气体双曲线相重合，如图2中的13 ℃以下的实际等温线均近似为双曲线．

解析表明，应用气体的玻尔兹曼因子方程，可以在定量上精确描述图2中C O2实验实测等温线段A B，A1a1，a1o1的变化规律．

（2）气液共存相变过程的数学描述

等温压缩C O2气体到达饱和点（如B点）之后，由于凝结核的作用而出现气体的液化，体系转变为由饱和气体与液化了的液体两个均匀部分共同组成，且液体所受到的压力等于饱和蒸气压．对于总体积为V，总质量为摩尔质量M的气液共存体系，等温压缩时的气液相变过程，可由分别描述气体与液体的两个玻尔兹曼因子方程式（1）、式（3）（即饱和蒸气物态方程及液体的物态方程）组成的下列方程组来描述

其中式（9）为质量守恒方程，式（10 ）为体积方程．

式（1）与式（3）相加，得

在温度较低（如13 ℃）时，等温压缩气、液共存体系的过程中，饱和蒸气和液化了的液体内部的分子数密度都可以近似认为保持不变，也即两均匀体系内部相邻分子之间的平均间距都保持定值不变，饱和蒸气与液体各自的表面自由能Eg与Ei也保持定值不变．也就是说，达到饱和点B之后的等温压缩过程中，T，pg，Eg与Ei都保持定值不变．故对式（11 ）两边微分得

由于式（9）两边微分得

dmg＝d M－dmi＝－dmi

所以

由于T，pg，Eg与Ei均为定值，且

故此式（12 ）可改写为

其中D1为常量，且D1≥0．由直线方程式（13 ）可知，在气体达到饱和点B之后的等温压缩过程中，体系的饱和蒸气压保持不变，总体积随着液化质量mi的增加等比率地减小，这一过程持续到气体全部液化时（即mi＝M）的C点为止．等温压缩线如图2（或图1）中气液相变的直线段B C所示．

在图2中，B点代表饱和蒸气开始液化尚未液化的起始点，B点的横坐标就是饱和蒸气的摩尔体积Vgm；C点代表的是饱和蒸气全部液化的终止点，C点的横坐标就是液体的摩尔体积Vim．由于随着等温压缩温度的升髙，饱和蒸气的分子数密度会增加，Vgm变小，液体的分子数密度会减小，Vim变大，所以，在图2中气液相变的直线段B C会随着等温压缩温度的升髙而缩短，如图2中与B C近似平行的直线段所示．当温度升高到临界温度Tc（31 ．1℃）时，Vgm＝Vim，B C线段缩短变为一个点，即临界点K．

必须指出，在温度T趋近于临界温度Tc条件下等温压缩气液共存体系的过程中，饱和蒸气压与气体、液体内部分子数密度的变化将不再是可以忽略的，饱和蒸气的pg，Eg会随着等温压缩过程而变大，液体的Ei会随着等温压缩过程而变小，式（13 ）中的因子也会随着压缩过程而不断变小．也就是说，随着压缩过程的进行，液化质量dmi的等量增加所导至的总体积V的减小量dV，会越来越小．等温压缩会变得越来越困难，等温压缩的液气线段将不再与较低温度时的直线段平行，会发生相应向上偏移的变化，如图2中21 ℃等温线中a1o1线段所示意．

解析表明，应用气体的玻尔兹曼因子方程式（1）与单元液体的玻尔兹曼因子方程式（3）组成的方程组，可以在定量上精确描述图2（或图1）中等温压缩C O2气液共存体系时的直线变化规律，从而，实现了用简洁的数学语言精确描述气液相变的目标．

3．4 临界系数趋同性的数学描述

由于在临界点上，Vgm＝Vim＝Vgmc，故描述临界点C O2摩尔气体体系的玻尔兹曼因子方程式（2）变为

由式（14 ），C O2气体的临界系数可表示为临界玻尔兹曼因子的倒数，即

代入数据得

Kk≈e1．250＝3．490 （气体公共的临界系数）

进一步对“气体数据手册［6］”中所列156 种气体（除空气外，其余155 种均为单一纯气体产品）进行实际计算考察表明，气体公共的临界系数3．490 相对于156 种气体临界系数Kk的实验值，相对误差小于5%的气体有81 种；小于10 %的有123 种；而小于20 %的有147 种．分别占气体总数的51 ．92 %，78 ．84 %与94 ．23 %．相对误差大于20 %的气体仅9种，只占气体总数的5．77 %．这一事实也有力地说明了，实际气体的临界系数虽然与范氏理论给出的“普适常量2．667 ”相差甚大，但确实存在趋同的特性．这也就是说，若将支配临界玻尔兹曼因子的参量定为经验常量1．25 ，则在20 %误差范围之内，有94 ．23 %的各种类型气体的临界系数都可以近似认为是相同的，为临界玻尔兹曼因子的倒数，即

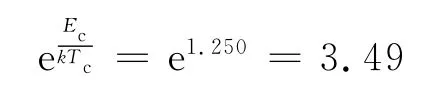
3．5 气体全部液化之后的C O2实验实测等温线的数学描述

由于等温压缩气液共存体系至C点时，mi＝M，即气体已全部液化，再进一步压缩时，液体所受到的压力将由饱和蒸气压pg转变为外力对液体体系的压力pi．随着pi的增大，液体体积变小，液体内部两相邻分子间的平均间距r也就迅速由趋近、等于r0，变为小于r0，相邻分子间相互作用的合力即随之转化为强大的斥力，Ei也就随之由大于零转变为小于零，且其绝对值随着Vim的减小而急剧增大，描述摩尔单元液体体系的玻尔兹曼因子方程变为