基于Matlab 的可调磁力减振镗杆控制系统参数优化*
2014-06-29罗红波
陈 可,李 伟,罗红波
(四川大学 制造科学与工程学院,四川 610000)
0 引言
镗杆是镗削加工工艺系统中刚性最薄弱的环节。目前一些已有的一些对于镗杆的研究已经系统地研究了内置式动力单减振、双减振镗杆,设计出了减振性能良好的镗杆,获得了相应的成果,但是这些内置式减振镗杆也存在一些不足:
(1) 弹性支承元件橡胶圈容易疲劳老化,且耐热性欠缺,容易失去设计刚度值;
(2) 橡胶圈与阻尼液直接接触,易被腐蚀;
(3) 阻尼液的粘度受温度影响明显,阻尼值容易减小;
(4) 需要考虑阻尼液的密封,镗杆在镗削过程中在不停地振动,容易泄漏,对密封性能要求高。
因此提出利用电磁场提供的刚度阻尼代替橡胶圈和阻尼液,设计一种新型动力减振镗杆,克服上述内置式动力减振镗杆的不足。
1 控制系统数学模型建立

图1 磁力减振镗杆结构示意图
可调磁力减振镗杆的结构如图1 所示,镗杆体内有高密度大质量的减振块4,减振块两端安装有减振块铁芯7,减振块铁芯外是电磁铁6。镗削加工时,电磁铁通电产生磁场,减振块铁芯在磁场作用下受到电磁吸力,电磁铁中通过适当的电流,上端的电磁吸力大于下端电磁吸力,使减振块悬浮在镗杆体中,即磁支承,并提供设计的刚度阻尼,达到动力减振目的。只要结构参数和控制参数设置得当,就可以使镗杆具有很好的减振性能。
磁力减振镗杆中电磁力主要是由电磁铁为减振块提供适应减振要求的刚度和阻尼,因此拟采用四个独立的单自由度控制系统来进行磁力减振镗杆的电磁铁控制系统简化。磁力减振镗杆是利用电磁铁产生的电磁力使减振块悬浮于镗杆的减振腔中,在镗杆工作过程中,减振块受到外力干扰会离开平衡位置,此时需要电磁力作用把减振块吸回原来的平衡位置,因此比较好的设计方案是电磁铁绕圈采用差动联接方式。磁力减振镗杆一个自由度的电磁力控制系统结构如图2 所示。

图2 磁力减振镗杆电磁铁差动控制示意图
这种设置使得电磁铁能够在两个方向上对减振块铁芯产生磁力,整个磁力减振镗杆由四个这样的磁力控制系统构成。此控制系统是采用的差动联接,设减振块在坐标正方向有位移,减振块x方向电磁力与电流和位移的关系推导如下:
在图2 所示的差动联接励磁方式下,磁极1 的励磁电流为偏置电流io与控制电流ix之和io+ix,磁极2 的励磁电流为偏置电流与控制电流ix之差io-ix。磁极1 处的气隙为设计气隙s与气隙变化量x之差s-x,磁极2 处的气隙为设计气隙x与气隙变化量x之和s+x。减振块受到的电磁力线性化后为:
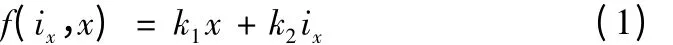
式中
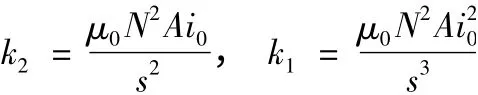
假设干扰力p(t)=0 ,可得

对上式进行拉普拉斯变换,得
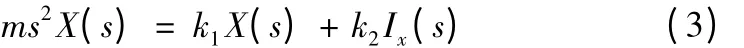
即可得到磁力减振镗杆电磁铁以位移X为输出,电流I为输入的传递函数模型

磁力减振镗杆电磁铁闭环控制框图如图3 所示,此控制系统由控制器Gc(s)、功率放大器Ga(s)、传感器Gb(s)和对象模型G(s)组成。对象模型就是磁力减振镗杆电磁铁和减振块组成的被控对象。
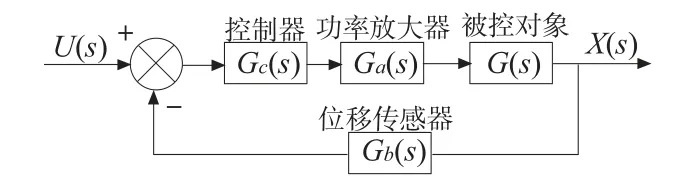
图3 磁力减振镗杆电磁铁闭环控制示意图
控制方式采用目前工业上广泛应用的PID 控制,其结构改变灵活,参数调整方便,在工业控制过程中效果显著且易于实现。控制器的传递函数为[10]
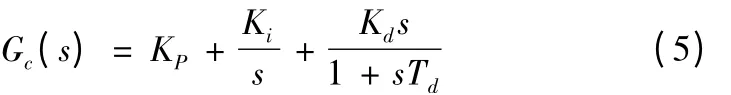
式中,Kp为比例系数,KI为积分系数,KD为微分系数,Td为微分时间常数。由于微分时间常数很小,可以忽略不计,因此式(5)可以简化为:

由此可建立如图3 所示的计算机闭环控制系统框图。框图中为使用计算机控制增加了A/D 转换器及D/A 转换器,设A/D 转换器增益为Kad,D/A 转换器增益为Kad。
将PID 控制的磁力减振镗杆等效于一般的弹簧阻尼减振镗杆,则
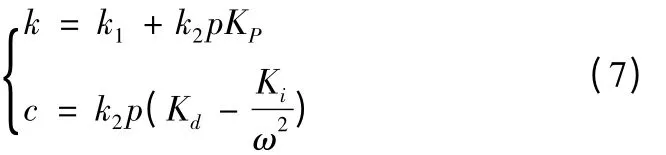
式(7)即为磁力减振镗杆时域刚度和时域阻尼与控制系统参数之间的函数关系。由式子可见只要结构和控制系统设计得当,就可以得到所需要设计的刚度和阻尼。
2 控制系统仿真
根据磁力减振镗杆的计算机闭环控制示意图3,可以在数学软件Matlab 的Simulink[10]进行控制仿真。此时PID 控制器参数及被控对象参数都还是未知量,镗杆设计时一对磁极面积,线圈匝数,气隙,减振块质量,偏置电流。假设PID 控制器比例系数取,积分系数取、微分系数;增益系数取P=2.0,增益系数取Q=10。由式f(ix,x)= k1x + k2ix
可以计算出k1=5.026×104N/m,k2=33.51A/m。称以上参数赋值为赋值1。给控制系统参数赋值后,可在Simulink 中进行仿真了。假设减振块此时有一个幅值为0.2mm 的振动,模拟控制系统此时作出的响应。这个振动可以用一个阶跃信号表示,其作用时间步为5e -5s,初值为0.0002m,终值为0。系统响应如图4 所示

图4 赋值1 时控制系统阶跃响应曲线
由图可见在控制系统参数在赋值1 时,PID 控制能够使系统回复平衡位置附近,但系统静、动态误差大,因此需要对控制系统的参数进行优化,包括三个方面:
1)PID 控制器的三个参数,分别为比例系数KP,积分系数Ki和微分系数Kd;
2)D/A 转换器增益为Kda与功率放大器的增益Aa之积增益系数P;
3)A/D 转换器增益为Kad与功率放大器的增益Aa之积增益系数Q;
3 控制系统参数优化
由仿真分析可以看出PID 控制器参数对控制效果有直接的影响,如果控制参数取得不当时,对系统的控制性能十分不利。这些控制参数必须要进行适当的调整,使得控制系统性能最优化。优化的目的是希望整个控制系统具有良好的动态、静态特性,使系统具有很好的稳定性,并且要求响应速度快,超调量小。在这里我们选用ItAE 误差函数,
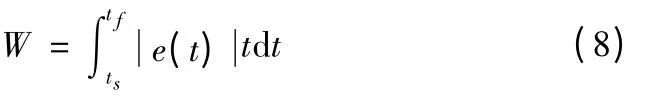
优化目标就是使式(8)W取得最小值。将其描述为数学模型:
目标变量:Kp、Ki、Kd、P、Q;
优化目标:优化函数取得最小值;
约束条件:100 ≤Kp≤5000 ,100 ≤Ki≤50000 ,
而根据减振块的刚度阻尼要求,即要使磁力减振镗杆刀尖相对振幅获得较小值时,根据在Maple 中编写好优化程序计算得到修正后的参数a =0.79 ,u =0.20 ,ζ1=0.09 ,ζ2=0.23 ,计算可得k =3.2×105N/m,c=753.48N·s/m。根据式(7),可以得到Kp,Ki,Kd,P,Q,i0之间的约束关系为:
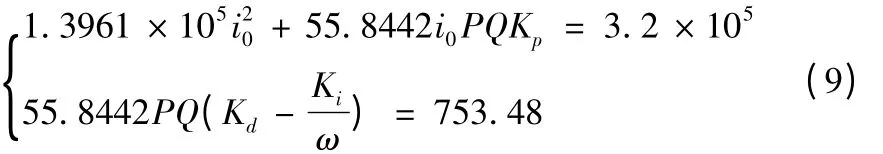
式中,ω 为刀尖受到外界激振力频率。由于当外界激振力频率与镗杆体固有频率相等时会产生共振,振幅将会达到最大值,因此设计时ω 取镗杆固有频率值,使减振镗杆在这个频率的外界激振力作用下也能够有较好减振性能。即取

在上述优化数学模型中还应该加入式(9)的等式约束。
这个优化过程可以利用Simulink 与Matlab 优化工具箱相结合进行优化。首先在Simulink 中绘制控制系统与误差函数模型,由于要对系统参数进行优化,而在Simulink 中各模块参数是Simulink 里的局部参数,不能传递到Matlab 工作空间中,因此需要对各参数所在子系统进行封装,以便能够设置成全局变量进行优化。图中PID 框为PID 控制器子系统的封装,设置Kp、Ki、Kd为参数;CLTG 框为磁力减振镗杆电磁铁子系统的封装,设置偏置电流io为参数;P框为增益封装,设置P为参数;Q框为增益封装,设置Q为参数。
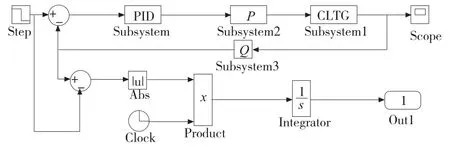
图5 控制系统参数优化模型
设置好参数后,就可以利用Matlab 的优化工具箱中的有约束优化函数fmincon()进行参数优化。
程序编制好后,直接在Matlab 中运行,即可根据ItAE 准则得到一组优化参数。

用优化的控制参数进行仿真,可以看到控制系统具有较小的超调量,较快的响应速度和动、静态稳定性。如图6 所示。
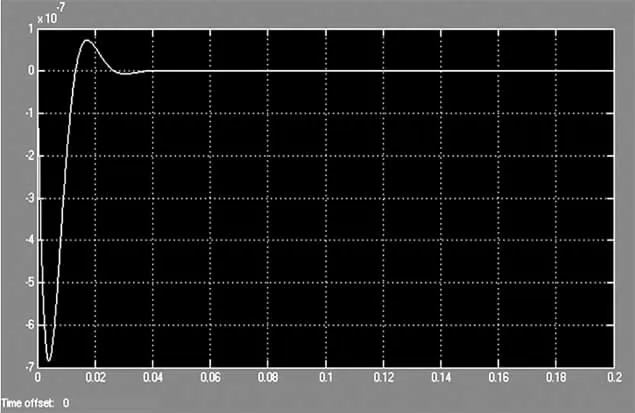
图6 优化后系统响应曲线
4 结论
通过建立可调磁力减振镗杆的控制系统模型,并经过对磁力减振镗杆减振块刚度阻尼与传统弹簧阻尼液刚度阻尼的等效,利用Matlab 中Simulink 模块及优化工具箱,根据ItAE 准则,得到一组优化的控制参数KP =590 、Ki =540.77 、Kd =3.3 、P =2 、Q=8.04。
利用此优化参数进行仿真,可以看到控制系统具有较小的超调量,较快的响应速度和动、静态稳定性,控制参数影响可调磁力减振镗杆减振块的刚度阻尼,最终影响镗杆的减振性能,说明此优化方法是可行的。
[1]LEE D G,YUN HWANG H,KOOK KIM J. Design and manufacture of a carbon fiber epoxy rotating boring bar[J].Composite Structures,2003,60(1):115 -124.
[2]EDHI E,HOSHI T. Stabilization of high frequency chatter vibration in fine boring by friction damper[J]. Precision engineering,2001,25(3):224 -234.
[3]NAGANO S,KOIZUMI T,FUJII T,et al. Development of a composite boring bar [J]. Composite Structures,1997,38(1):531 -539.
[4]于德介,程军圣,杨宇. 机械振动学[M]. 长沙:湖南大学出版社,2010.
[5]王民,区炳显,昝涛,等. 镗杆颤振控制技术发展综述[J]. 北京工业大学学报,2011,37(8):1143 -1147.
[6]秦柏. 深孔加工动力减振镗杆的动力学仿真与参数化分析[D]. 哈尔滨:哈尔滨理工大学,2006.
[7]罗红波,李伟,唐才学. 内置式双减振镗杆动力学模型参数优化[J]. 四川大学学报(工程科学版),2012,44(5):207 -212.
[8]齐涤非. 镗削加工中的冲击式减振器减振性能研究[J].湘潭矿业学院学报,1999,14(2):70 -74.
[9]杨夷梅,杨玉军. 分支定界算法优化研究[J]. 中国科技信息,2008,21(1):42 -43.
[10]姚俊,仿真技术,马松辉. Simulink 建模与仿真[M].西安电子科技大学出版社,2002.
[11]王军,徐龙祥. 无传感器磁轴承转子位置自检测原理研究[J]. 传感器世界,2004,10(11):22 -24.
