双丝杠驱动直线进给系统动态特性分析*
2014-06-29丁喜合袁军堂汪振华董香龙
丁喜合,袁军堂,汪振华,董香龙
(南京理工大学 机械工程学院,南京 210094)
0 引言
双滚珠丝杠驱动直线进给系统具有良好的抗振性、高系统刚度以及快速系统响应性等优点[1-2],能够有效地抑制数控机床在高速和高加减速情况下产生的振动,因此其在高速和高精类数控机床中的应用日益广泛。
国外学者在双丝杠驱动的理论和实践方面有着较为深入的研究[1-2],日本森精机公司最早提出了双丝杠驱动的概念并将其应用于数控机床,有效地提高了机床的进给速度和加减速度,进而保证了加工精度。在国内,关晓勇[3]和严江云[4]等人建立了双驱动的动力学模型,从理论上证明了双丝杠机构能够抑制各轴驱动时产生的回转振动和弯曲。周勇[5]和郭崇嵩[6]等人建立了双丝杠驱动的有限元模型并进行了动态特性仿真分析,验证了双驱动相对于单驱动的优势。然而,这些研究在动力学特性方面还相对不足。此外,国内在双驱动进给系统设计时,多数参照国外机床,以经验法和类比法作为主要设计手段,对于影响双驱动进给系统动态特性的因素缺乏研究。因此,深入研究双丝杠驱动直线进给系统的动态特性及其影响因素,具有十分重要的意义。
本文以数控机床双滚珠丝杠驱动直线进给系统为研究对象,采用单因素分析法,建立其ANSYS 有限元模型并进行动态特性分析,同时,基于二自由度系统振动模型分别研究丝杠跨距和导轨跨距对进给系统动态特性的影响规律,为双丝杠进给系统的设计提供理论参考。
1 双丝杠驱动直线进给系统模型简述
文中共建立了10 组双丝杠驱动直线进给系统有限元模型。采用单因素分析法,分别研究丝杠跨距和导轨跨距对进给系统动态特性的影响规律,其中,滚珠丝杠全长1600mm,直径为50mm。
在导轨跨距D不变,取1300mm 时,丝杠的跨距依次取值300mm、450mm、600mm、750mm 和900mm,记为S300、S450、S600、S750和S900。在丝杠跨距S不变,取1050mm 时,导轨的跨距依次取值150mm、300mm、450mm、600mm 和750mm,记为D150、D300、D450、D600和D750。
为保证分析结果的可比性,在建立有限元模型时,对各模型采取相同的单元类型、实常数、简化方式和网格划分方式。整个结构实体单元类型选择solid187 单元。采用自由网格划分。
结合面建模时,选用MATRIX 27 弹簧阻尼单元来模拟固定结合面和滚动结合面的连接[7-9],结合面的参数为本课题组针对相应型号和规格的部件试验测定,具体数值如表1 所示。图1a 和图1b 分别为S300和D300的有限元模型。
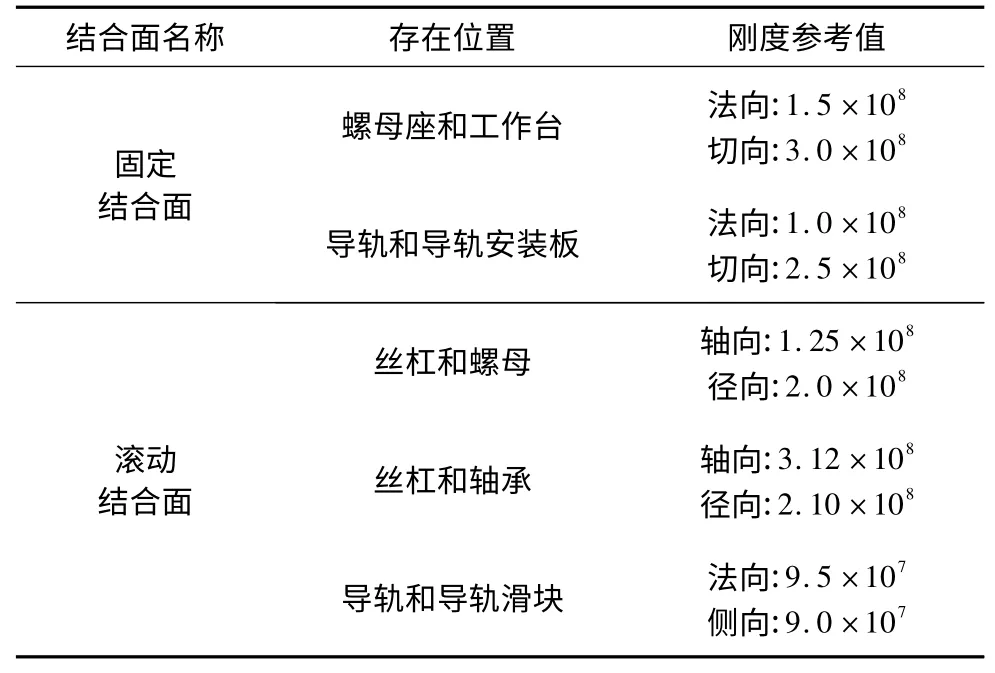
表1 各结合面弹簧阻尼单元刚度参考值
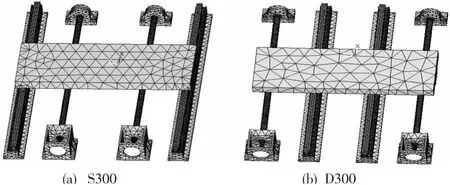
图1 S300和D300进给系统有限元模型
2 丝杠跨距对进给系统动态特性影响
低阶模态对进给系统工作时影响最大,高阶模态振型复杂,远离工作频段,因此这里只关注系统的低阶模态。在ANSYS 中采用BlockLanczos 模态提取法分别对S300、S450、S600、S750和S900进行模态分析。
有限元分析结果显示,系统的低阶模态主要表现为工作台沿三个方向的振动以及绕三个方向的扭转变形。比较相同振型下各组模型的固有频率值,如表2所示。其中,丝杠轴向为X向,工作台上表面法向为Z向,垂直于工作台侧面为Y向。
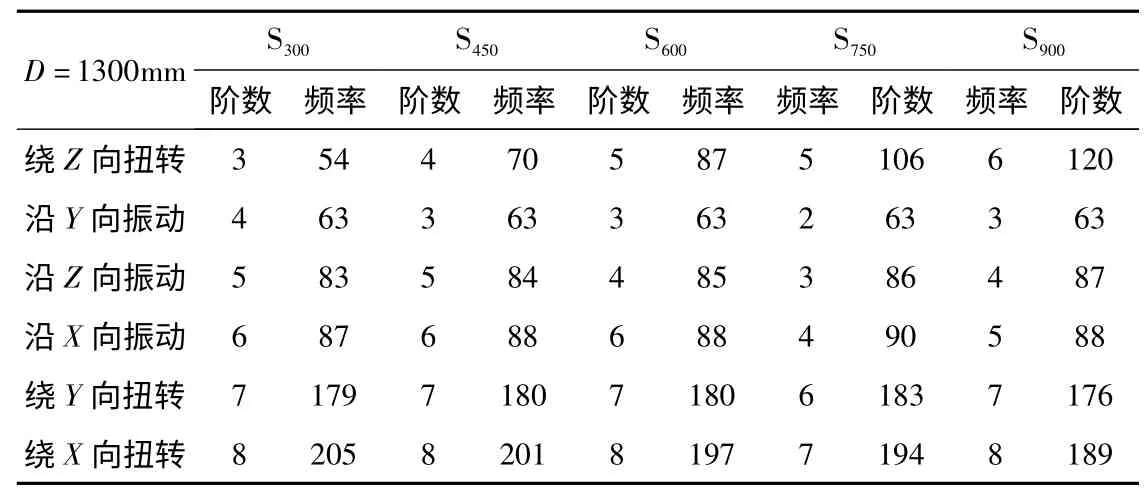
表2 S300、S450、S600、S750和S900各阶振型下的固有频率值
由表2 可知,在导轨跨距不变的情况下,丝杠跨距的改变主要影响工作台绕Z向的扭转振动,且随着丝杠跨距的增加,该振型下的固有频率上升明显,说明系统抑制扭转振动和变形的能力更强。图2 为S300 和S900 的工作台绕Z向扭转振动的振型图。

图2 绕Z 向扭转振动的振型图
产生这种现象的原因可以用系统的二自由度振动模型[10]来解释。滚珠丝杠副作为进给系统的传动部件,主要承受轴向力的作用,而滚动导轨由于摩擦系数很小(一般在0.0025 -0.005 之间),相对于滚珠丝杠和丝杠螺母的接触刚度,其进给方向的刚度可以忽略不计。同时,由于丝杠自身沿进给方向的拉压变形极小,忽略其影响。因此,以工作台为研究对象,其在进给方向上的动力学模型可简化为如图3a 所示的二自由度系统振动模型。
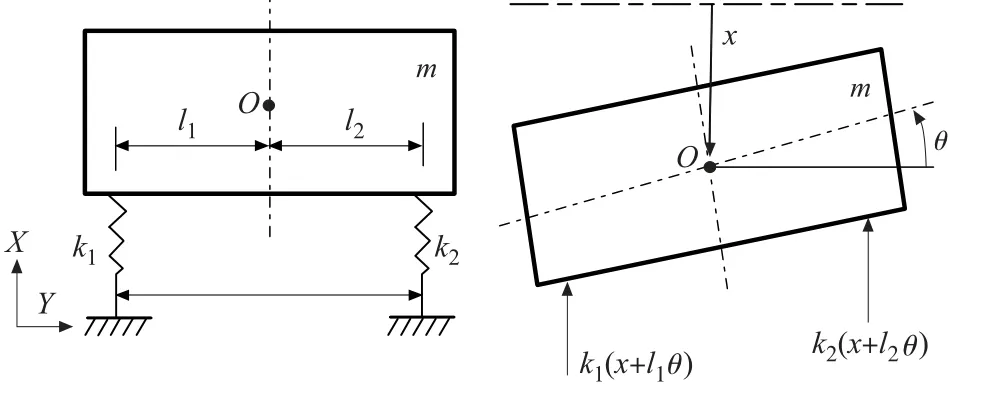
图3 工作台在进给方向上二自由度系统振动模型
设工作台质量为m,左、右两滚珠丝杠的间距为l,它们与工作台质心O的水平距离分别为l1和l2,滚珠丝杠和丝杠螺母的接触刚度分别为k1和k2。取工作台质心O沿X向坐标x和绕横向水平质心轴的转角θ为广义坐标。
设在某瞬时,质心O相对于静平衡位置移动距离为x,相应转角为θ,则左、右两弹簧的变形为(x+l1θ)和(x-l2θ),如图3b 所示。运动微分方程可表示为:
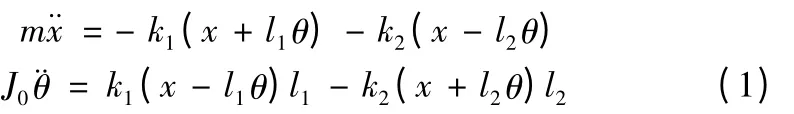
写成矩阵形式:

设x = Xsin(wt +φ),θ=Θsin(wt +φ),代入振动微分方程有:

特征方程为:
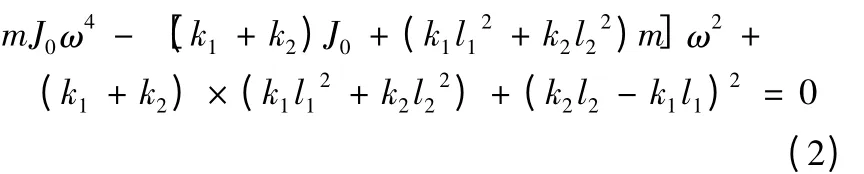
两滚珠丝杠采用相同的型号,故设k1= k2= k。它们相对于工作台中心对称布置,所以有代入式(2)得:

解特征方程式(3)得:
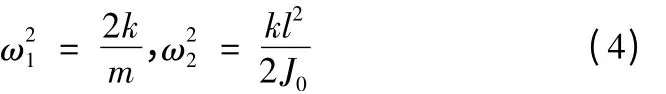
由式(4)可知,在进给系统进给方向上,工作台共有两阶固有频率,其中一阶为沿丝杠轴向的振动,另一阶则为绕工作台法向的扭转振动。
由于m和k为定值,所以沿丝杠轴向振动的固有频率ω1不随丝杠跨距的改变而变化,这正是表2 中工作台沿X向振动的固有频率基本没有产生变化的原因;同理,当k和J0为定值时,ω2随着丝杠跨距l的增大而变大,与表2 中工作台绕Z向扭转的固有频率随着跨距增加而不断提升相一致。
3 导轨跨距对进给系统动态特性影响
在ANSYS 中同样采用BlockLanczos 模态提取法对D150、D300、D450、D600和D750进行模态分析,研究导轨跨距的变化对进给系统动态特性的影响。
系统的低阶模态仍表现为工作台沿三个方向的振动以及绕三个方向的扭转变形。比较这些振型下各组模型的固有频率值,如表3 所示。其中,丝杠轴向为X向,工作台上表面法向为Z向,垂直于工作台侧面为Y向。
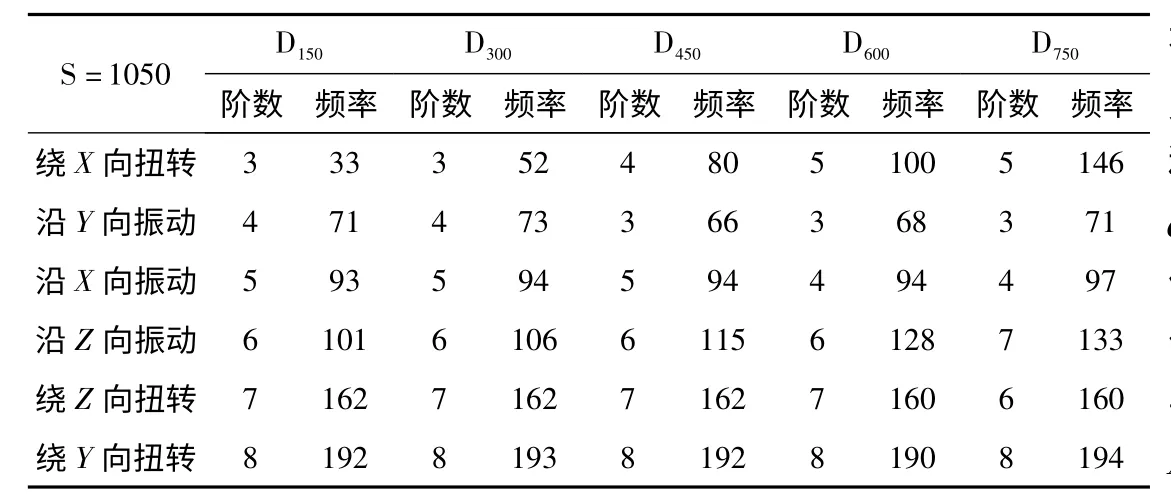
表3 D150、D300、D450、D600和D750各阶振型下的固有频率值
由表3 可知,在丝杠跨距不变的情况下,导轨跨距的改变主要影响工作台绕X向的扭转振动,且随着导轨跨距的增加,该振型下的固有频率越高,说明系统抑制扭转振动和变形的能力更强。图4 为D150 和D750的工作台绕Z向扭转振动的振型图。
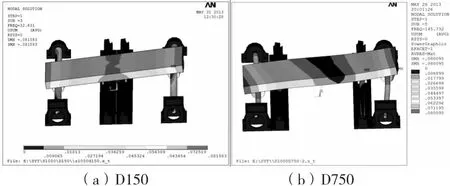
图4 D150 和D750 绕X 向扭转振动的振型图
产生这种现象的原因同样可以用系统的二自由度振动模型来解释。在工作台的法向方向(Z向)上,滚动导轨作为进给系统的主要支撑件,主要承受工作台法向力的作用,且滚珠丝杠属于大长宽比的杆件,容易产生径向变形,故相对于滚动滑块和导轨结合部的刚度,丝杠和丝杠螺母之间的径向刚度的影响可以做简化忽略处理。因此,以工作台为研究对象,在其法向上的动力学模型可简化为如图5a 所示的二自由度系统振动模型。
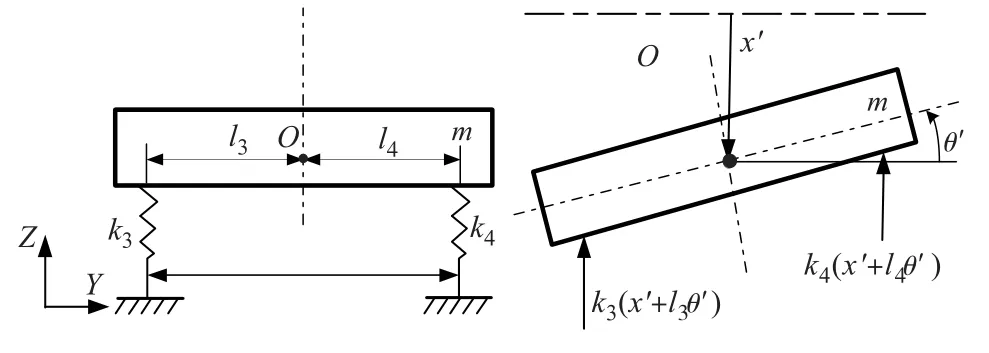
图5 工作台在其法向上的二自由度系统振动模型
设工作台质量为m,左、右丝杠间距为l’,它们距离工作台质心O的距离分别为滚珠丝杠和丝杠螺母的接触刚度分别为k3= k4= k'。质心O相对于静平衡位置移动距离x’,相应的转角为θ’。同理,可得其微分方程为式(5)。
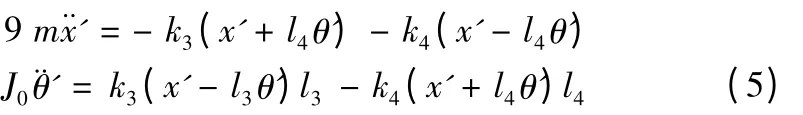
特征方程为:
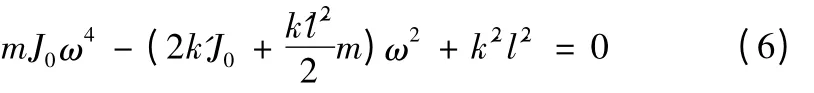
解得:
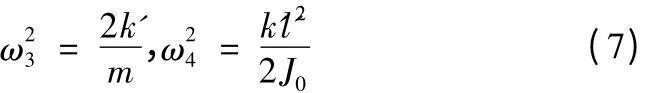
由式(7)可知,在工作台法向上,工作台共有两阶固有频率,其中一阶为沿法向的振动,另一阶则为绕丝杠轴向的扭转振动。由于m和k为定值,所以沿丝杠轴向振动的固有频率ω3不随导轨跨距的改变而变化,这与表3 中工作台沿Z向振动的固有频率基本没有产生变化相一致;同理,当k和J0为定值时,ω4随着导轨跨距l’的增大而变大,与表3 中工作台绕X向扭转的固有频率随着导轨跨距增加而不断提升相一致。
4 结论
(1)双丝杠驱动进给系统中,滚珠丝杠跨距的改变对系统绕工作台法向的扭转振动的影响较为明显,且随着丝杠跨距的增加,系统在相应振型下固有频率越高,其抵抗振动和变形的能力越强,动态特性越好。
(2)导轨跨距的改变对系统绕丝杠轴向的扭转振动的影响较为明显,且随着导轨跨距的增加,系统在相应振型下固有频率越高,抵抗振动和变形的能力也越强,动态特性越好。
因此,对于双丝杠驱动直线进给系统,在实际工况允许的情况下,应尽可能选择较大的导轨跨距和丝杠跨距。
[1]Hiramoto K,Hansel A,Ding S.A Study on the Drive at Center of Gravity(DCG)Feed Principle and its Application for Development of High Performance Machine Tool Systems[J].CIRP Annals Manufacturing Technology,2005,54(1):333-336.
[2]Mori Seiki Co.,Ltd. Machine Tool Driven by Center of Gravity[J].Seisanzai Maketeingu,2004.
[3]关晓勇,刘春时等.基于重心驱动的设计方法研究及其在高性能机床开发中的应用[J]. 中国机械工程,2011,22(18):2170 -2174.
[4]严江云,字立敏,余光怀.数控机床双滚珠丝杠进给驱动研究[J].制造技术与机床,2012(11):53 -55.
[5]周勇. 高速进给驱动系统动态特性分析及其运动控制研究[D].武汉:华中科技大学,2008.
[6]郭崇嵩,芮执元,刘军. 铣车加工中心双驱进给系统静动态特性分析[J].组合机床与自动化加工技术,2012(6):5-8.
[7]M.F.Zaeh,Th.Oertli et al.Finite Element Modeling of Ball Screw Feed Drive Systems[J]. CIRP Annals Manufacturing Technology,2004,53(1):289 -292.
[8]Kuan min Mao,Bin Li,Jun Wu. Stiffness Influential Factorsbase Dynamic Modeling and its Parameter Identification Method of Fixed Joints in Machine Tools[J]. International Journal of Machine Tools and Manufacture,2010,50(2):156-164.
[9]蒋书运,祝书龙.带滚珠丝杠副的直线导轨结合部动态刚度特性[J].机械工程学报,2010,46(1):92 -99.
[10]Singiresu S.Rao 著,李欣业,张明路编译. 机械振动(第四版)[M].北京:清华大学出版社,2009.
