基于三次多项式加减速的NURBS 插补前瞻控制算法*

张 力，杨东升，王允森，李海英

(1.中国科学院 沈阳计算技术研究所，沈阳 110168;2.中国科学院大学，北京 100049)

0 引言

目前，参数曲线(曲面)广泛应用于航空、模具等制造领域中，复杂曲线(曲面)的加工技术一直是研究的重点。NURBS 曲线插补也成为数控插补中一项重要技术，对于高速高精数控加工更是如此。在高速加工时，如果刀具的进给方向发生突变而进给速度没有及时降低，就会引起过切，所以在加工中又引入了前瞻技术，预先获得待加工零件轮廓进给方向的突变点及通过该突变点最佳进给速度等控制信息，使得当插补到这些突变点之前能及时修调进给速度，避免出现过切。目前，国内外对于前瞻技术进行了大量研究。Du等［1］提出了一种自适应的前瞻插补算法，在对速度进行自适应控制的同时进行前瞻控制，找出速度变化超过允许范围的敏感点，提前进行加减速规划。但是这种方法没有对加加速度进行控制。曹宇男等［2］设计了一种基于S 型加减速的前瞻控制算法，算法中设定了最大前瞻段数，并根据实际插补轨迹的几何特性实现了加减速的控制。但是在对复杂曲线进行加减速控制时，其前瞻距离的确定有一定的困难。彭芳瑜等［3］利用二次遗传算法对NURBS 曲线进行预处理，找到曲线上的曲率极大值点集，并建立机床动力学性能和曲线几何性能的混合约束条件，生成曲线插补的前瞻控制信息，实时优化进给速度。但对最优速度求解过于复杂且并不是全局最优解。Lin 等［4］提出了动态NURBS插补的前瞻算法，对加速度和加加速度受限的S 型加减速进行讨论，但是七段S 型曲线较为复杂，也不能保证加速度平滑。

本文在以上研究基础上，提出了一种三次多项式加减速型NURBS 曲线前瞻算法。该算法实现了加速度平滑，改善了加加速度突变次数过多问题。首先对加工曲线进行预处理，找到加工中的速度敏感点并对曲线分段，然后采用基于回溯的方法修正速度，保证系统能够减速到速度敏感点，然后对分段进行速度前瞻并保证加速度平滑过渡。最后对提出的算法进行仿真验证其可行性。

1 NURBS 曲线的定义

NURBS 曲线是基于分段有理B 样条多项式基函数定义的。一条k次的NURBS 曲线定义为:

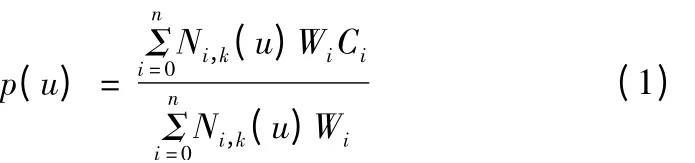
其中，u为NURBS 曲线的自变量，Ci(i=0，1…n)为控制顶点，共有n+1 个，wi(i=0，1…n)为控制顶点的权因子，其中首末权因子w0，wn＞0，其余wi≥0，Ni，k(u)是k次非均匀有理B 样条基函数，由节点矢量U=(ui，ui+1…ui+k)确定。

2 预处理

2.1 速度敏感点判别

速度敏感点应位于曲线的曲率极大值点处并且该插补点的曲率值大于设定阈值kthr，则该点为速度敏感点［5］。

其中Amax，F为系统允许最大加速度和最大进给速度。

2.2 速度敏感点处的最优速度求解

考虑以弓高误差对速度进行限制。用圆弧近似的方法来求出弓高误差与进给速度以及曲率之间的关系，如图1 所示，其中ρi为曲率半径，弓高误差为δ，设V(ui)为实际进给速度。

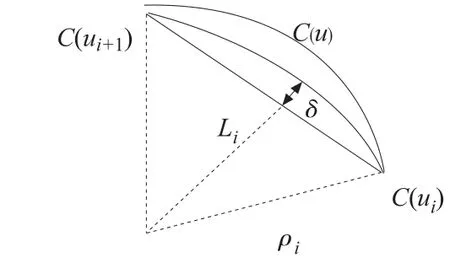
图1 高曲率点处的弓高误差

通过几何关系可以求出:

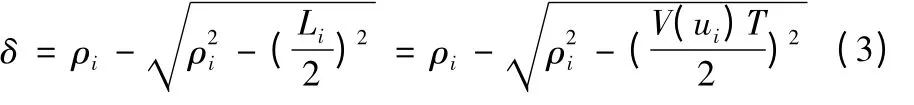
根据公式(3)，若假设加工所要求的最大弓高误差为δmax，则该误差约束下的速度Ve(ui)为:

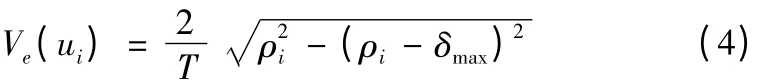
若设定加工时的编程速度为F，则实际的插补速度为:

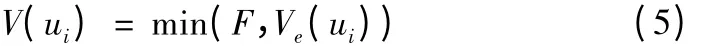
在预处理模块中，将曲线按速度敏感点把NURBS曲线划分为n段曲线，每一段的长度可以用下列公式得出:

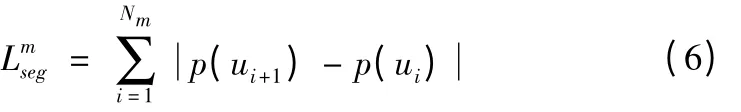
公式(6)中，m为每一段的标号，Nm为第m段曲线中插补点的个数。在预插补中求得分段开始和结束点处的最优速度、每段的最大速度Vmax以及每段的长度Lms eg存储在缓存中。

3 三次多项式型前瞻算法

3.1 三次多项式型加减速模型

对于三次多项式加减速，假设v(t)为速度曲线，a(t)为加速度曲线，j(t)为加加速度曲线，vs、ve分别为起点和终点速度，如图2 所示。此时速度曲线v(t)的表达式可写为［6］:

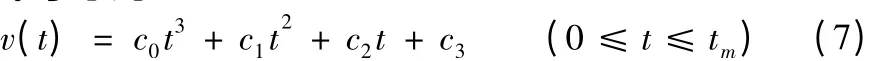
其中t为速度曲线v(t)的时间参数，tm为进给速度从vs变化到ve所需要的加减速时间。边界条件为:

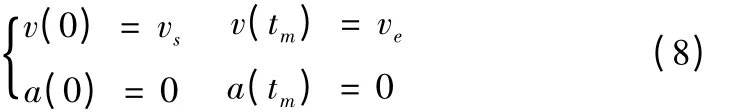
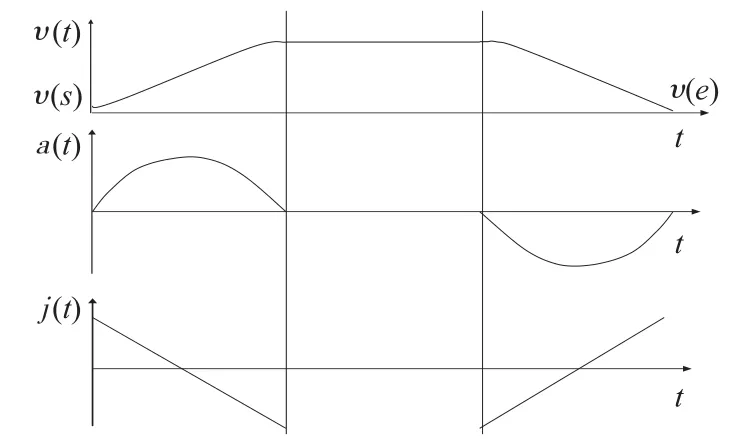
图2 三次多项式加减速模型

将公式(8)代入公式(7)速度曲线v(t)中可计算出四个系数为:

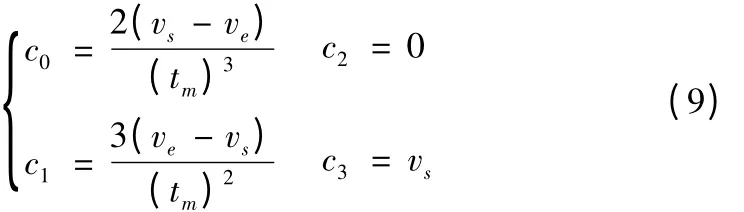
加速度曲线a(t)是以tm/2 为对称轴的二次曲线，因而其极值出现在tm/2 时。可得公式［7］:

可计算出进给速度从vs变化到ve所需的最短距离为:

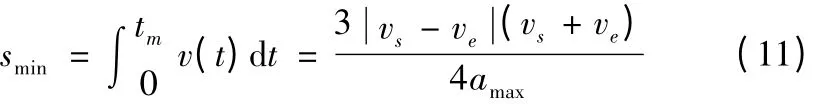
3.2 前瞻距离的确定

前瞻距离分为加工前瞻距离和预前瞻距离，加工前瞻距离为以当前点的速度能够减速到0 的距离，即预前瞻距离是消除后续的速度敏感点对前面速度变化的影响，即所以前瞻距离为［8］:

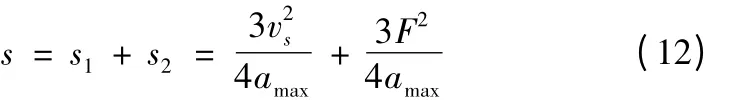
3.3 转接速度的修正

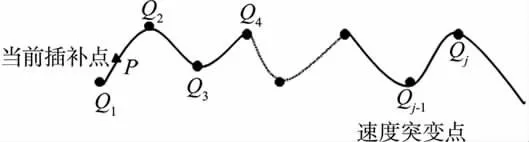
图3 转接点速度修正

根据速度突变点，将NURBS 曲线划分为曲线段，对已前瞻过的分段进行回溯修正，保证以当前点速度能够减速到其后的任意速度敏感点。对已前瞻的距离中需进行转接速度修正的j条轨迹段如图3 所示，P为当前插补点，Qj为前瞻的终点。其中vjmax为速度敏感点j处所允许的最大转接速度，sj-1j为轨迹段Qj-1Qj的长度，vjj-1为Qj处速度反向加速到Qj-1时获得的进给速度。具体过程如下［9］:

步骤1:对前瞻路径中的转接点进行速度修正，即以转接点处修正后的速度为起始速度反向加速到速度敏感点Qj-1处时所能获得的最大速度vjj-1为:

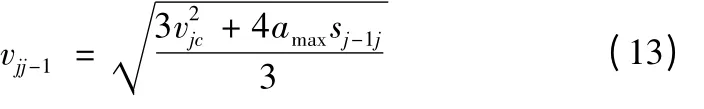
步骤2:判断vjj-1与Qj-1处所允许的最大速度vjmax之间的大小，则修正后的速度为:

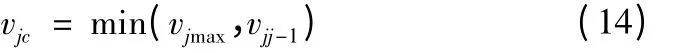
步骤3:判断j的大小。若过程还没到初始点，则j=j-1，转到步骤1 继续进行，若到初始点则结束回溯过程。

流程图如图4。

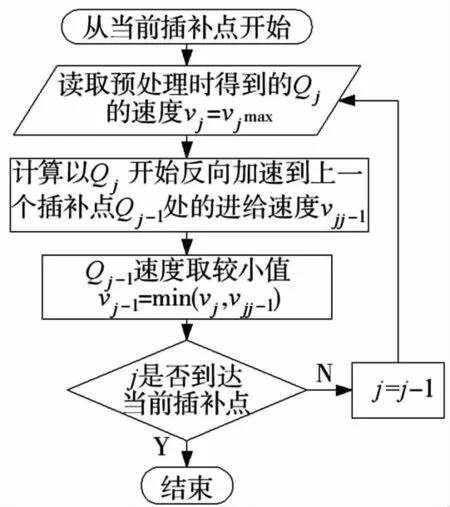
图4 速度修正流程图

3.4 进给速度的前瞻控制

加速阶段可以达不到段末处速度，但是减速阶段必须保证能够减速到速度敏感点。当加工剩余长度小于理论减速距离时则进入减速阶段。而本段减速区长度的计算和减速过程又由预处理中得到的该段起点、终点处的速度和段长决定。为简化计算，将减速点的求解转化对段内最大速度的求解［10］。从而得到减速所需的最短路径。设轨迹段为Q1Q2，长度为l12，v1c、v2c分别为速度敏感点Q1、Q2处修正后的最优速度。以下分六种情况进行讨论。

(1)速度、加速度曲线如图5a 所示，Q1Q2之间为加速阶段。判别条件为①v1c＜v2c，②v2c≥v12。v12为加速到点Q2处所能达到的最大理论速度:

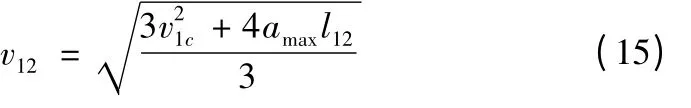
进给速度曲线v(t)的表达式为:

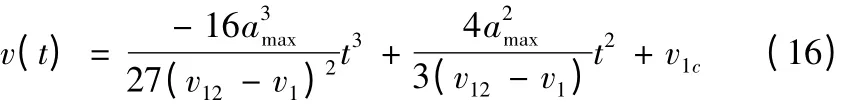
(2)速度、加速度曲线如图5b 所示，Q1Q2之间存在加速和减速过程。判别条件为①v1c＜v2c，②v2c＜v12，③vm＜Vmax。v12的值为公式(15)，vm为段内所能达到的最大理论速度，Vmax为预处理中记录的本段最大速度。

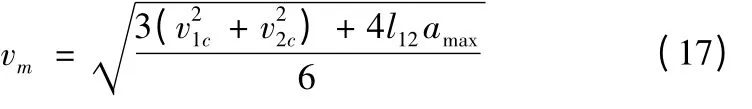
则t1点处即为减速点，则理论减速距离为:

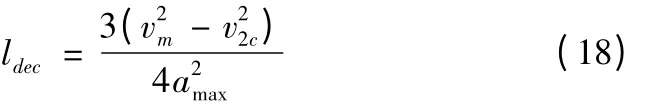
(3)速度、加速度曲线如图5c 所示，Q1Q2之间还存在匀速过程。判别条件为①v1c＜v2c，②vm≥Vmax。vm的值为公式(17)。则t2处即为减速点，最大速度达到预处理中记录的最大速度值。则理论减速距离为:

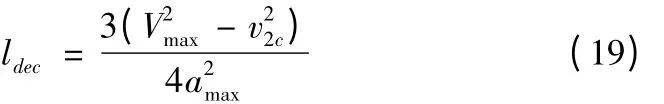
用v1dec2表示Q1减速到Q2处所能获得的最小速度公式为:

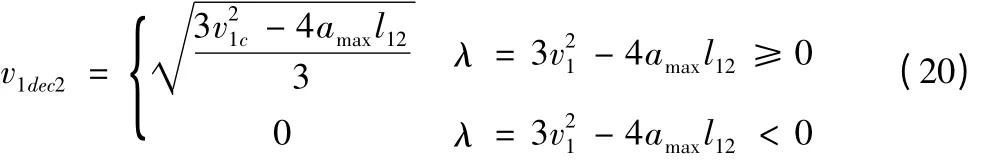
经过转接速度的修正，进给速度v2c＜v1dec2这种情况不存在。

(4)速度、加速度曲线如图5d 所示，本段为减速段。判别条件为①v1c＞v2c，②v2c=v1dec2，③λ ≥0 。本段为减速阶段，进给速度曲线为:

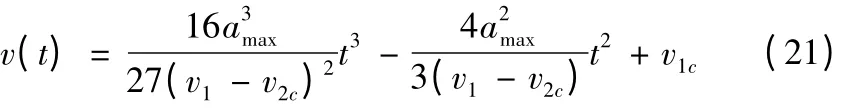
(5)速度曲线如图5e 所示，判别条件为①v1c＞v2c，②v2c＞v1dec2或者λ＜0 ，③vm＜Vmax。vm的值为公式(17)。t1点为减速点，计算公式和情况(2)中公式类似。

(6)速度曲线如图5f 所示，判别条件为①v1c＞v2c，②v2c＞v1dec2或者λ＜0 ，③vm≥Vmax。t2点为减速点，计算公式和情况(3)中公式类似。

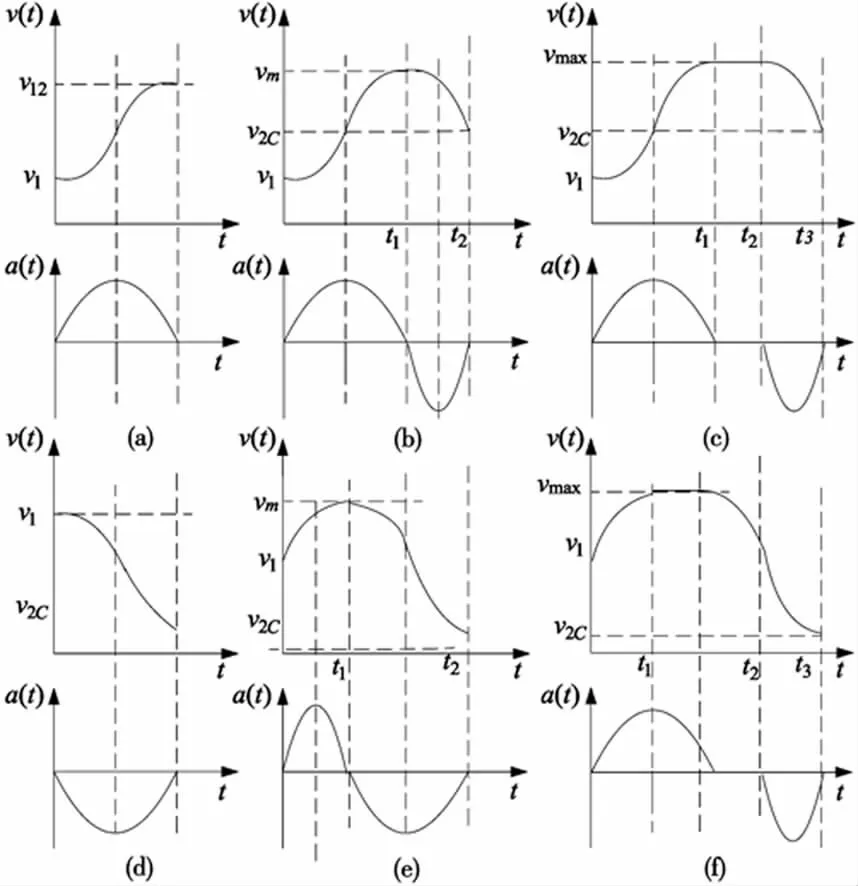
图5 速度和加速度曲线

4 实验仿真验证

为了验证算法的可行性，选择二维的NURBS 曲线进行仿真，如图6 所示，曲线参数如表1。仿真时编程速度为F=200mm/s，插补周期为T=2ms，最大加速度为A=0.0005m/s2，最大加加速度J=0.00004m/s3，最大弦高误差为Emax=0.0004mm。

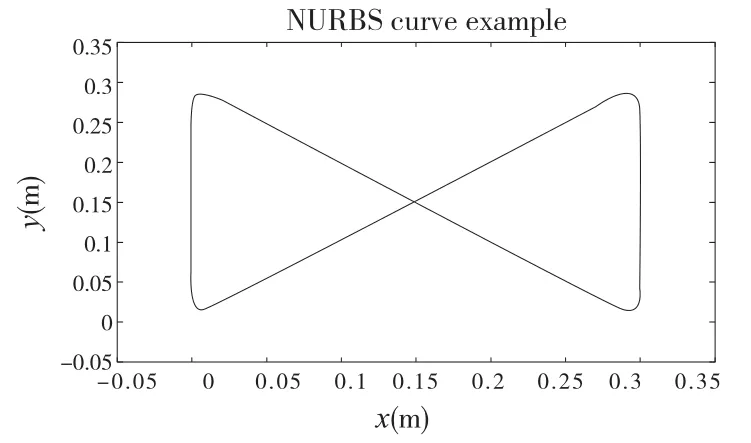
图6 NURBS 曲线

表1 NURBS 曲线参数列表

本文算法误差曲线如图7 所示，算法满足加工的精度要求，即所有插补点的弓高误差都控制在Emax以内，算法具有可行性。

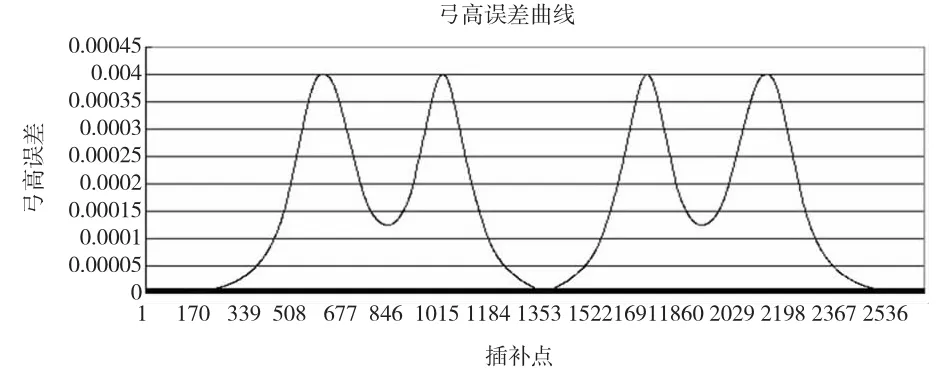
图7 本文算法的弓高误差

对比本文算法在加速度和加加速度方面的优点，选取S 型加减速前瞻算法进行对比。本文提出的算法在插补过程中，进给速度限制在编程速度F内，加速度和加加速度也都限制在最大加速度A和最大加加速度J的范围内，如图8a 所示，本文算法和S 型加减速前瞻算法都能够保证在速度敏感点前提前减速，敏感点处速度优化良好，能实现速度平滑变化。图8 b～e 中的加速度曲线和加加速度曲线可以看出本文算法的优点，仿真的曲线包含减速段、匀速段和加速段，图8b 显示本文算法在减速段和加速段的加速度曲线能实现平滑变化，而图8c中S 型加减速前瞻算法只能保证加速度曲线连续变化。加速度代表了机床的受力情况，加速度的平滑变化保证了机床的受力均匀变化。图8d 显示本文算法的加加速度局部连续变化，而图8e 中S 型加减速前瞻算法突变次数较多，具体的在一个加减速阶段内，S 型加减速前瞻算法的加加速度突变次数比本文算法多两次。而加加速度代表的是机床受力的变化频率，突变次数较多必然给机床带来更大冲击，引起更大的误差。

实验结果验证了本文算法的正确性和有效性，可以保证加工时的速度平滑变化，减少加加速度突变，减小了机床振动，符合柔性加工的要求。证速

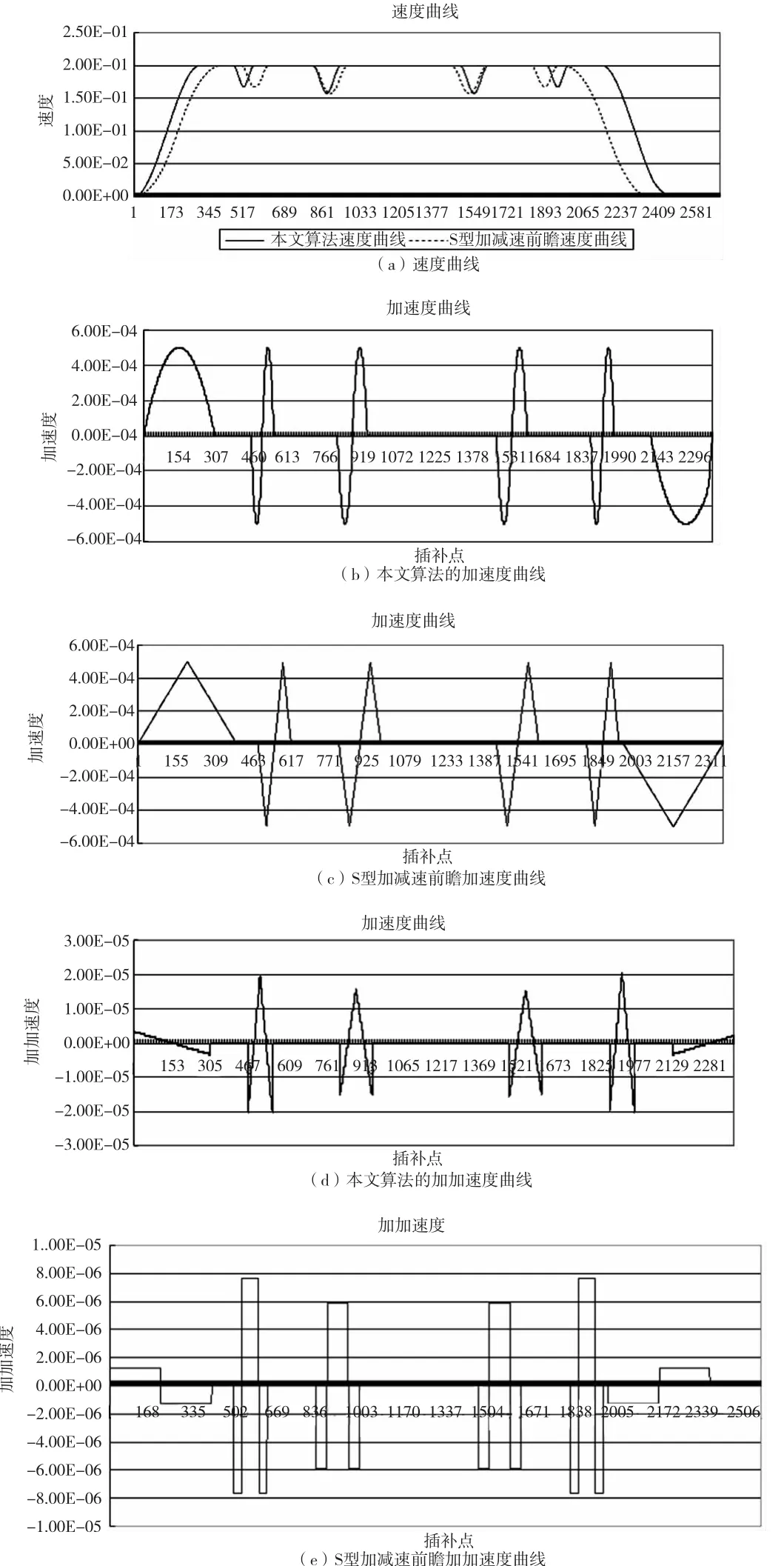
图8 仿真结果对比图

5 结束语

在研究了各种前瞻算法的基础上，提出了一种针对NURBS 曲线的基于三次多项式型加减速前瞻控制算法，算法能够提前预测速度敏感点，并依据速度敏感点类型来计算转接点处的最优速度。前瞻步骤可以分为前瞻路径的确定，速度敏感点处的速度回溯以及对回溯完的路径进行速度前瞻控制。所提出的前瞻算法能保度连续、加速度在加减速过程中连续变化并且减少了加加速度在一个加减速过程中的突变次数，避免突变给机床造成的振动。

［1］Du Daoshan，Liu Yadong，Yan Cunliang，et al.An Accurate Adaptive Parametirc Curve Interpolator for NURBS Curve Interpolation. ［J］. Int Adv Manuf Technol，2007，32:999 -1008.

［2］曹宇男，王田苗，陈友东，等. 插补前S 加减速在CNC 前瞻中的应用［J］. 北京航空航天大学学报，2007，33(5):595 -995.

［3］彭芳瑜，何莹，李斌.NURBS 曲线高速插补中的前瞻控制［J］. 计算机辅助设计与图形学学报，2006，18(5):625 -629.

［4］Ming Tzong Lin，Meng Shiun Tsai，Hong Tzong Yau，et al. Development of a dynamics-based NURBS interpolator with real-time look-ahead algorithm［J］. International Journal of Machine Tools ＆ Manufacture ，2007，47 :2246 -2262.

［5］Meng-Shiun Tsai，Hao Wei Nien，Hong-Tzong Yau. Development of an integrated look-ahead dynamics-based NURBS interpolator for high precision machinery.［J］. Computer-Aided Design，2008 ，40:554 -566.

［6］冷洪滨，邬义杰，潘晓弘. 三次多项式型微段高速自适应前瞻插补方法［J］. 机械工程学报，2009，45(6):73 -79.

［7］冷洪滨，邬义杰，潘晓弘.三次多项式型微段高速加工速度规划算法研究［J］. 计算机集成制造系统，2008，14(2):336 -340.

［8］王海涛，赵东标，高素美. 参数曲线的自适应实时前瞻插补算法［J］ . 计算机集成制造系统，2010 (16):386 -389.

［9］徐志明，冯正进，汪永生，等. 连续微小路径段的高速自适应前瞻插补算法［J］. 制造技术与机床，2003(12):20 -23.

［10］Lin Wang，Jianfu Cao. A look-ahead and adaptive speed control algorithm for high-speed CNC equipment［J］. Int J Adv Manuf Technol ，2012，63:705 -717.