基于多种群遗传算法的路径柔性车间调度问题*

李运霞，杜 娟，孙王路

(太原科技大学 机电学院，太原 030024)

0 引言

路径柔性的车间调度问题作为传统作业车间调度问题(Job-shop Scheduling Problem，JSP)的扩展，具有灵活性、复杂性、约束性、非线性、多极小性等特点。路径柔性车间调度作为工艺柔性的一个分支，在现代制造业中具有重要的应用价值和理论意义，是亟需解决的一类调度问题。

路径柔性的作业车间调度问题减少机器约束，增加工序可选机器的不确定性，是复杂的强NP 难题。目前，国内外对此问题进行了多方面的研究，并取得了一定成果。邵斌彬等［1］提出柔性车间的基于综合分派规则的快速启发式调度算法;贺仁杰等［2］提出用知识型协同演化方法求解柔性车间作业调度问题，优化性能良好;王万良等［3］针对局部收敛问题将粒子群法进行改进，求解柔性车间作业调度问题;Seyed Habib A.Rahmati［4］针对柔性作业车间调度，提出生物地理优化算法(BBO);遗传算法［5-7］在柔性车间调度中也取得了一定成果。针对路径柔性的作业车间调度特点以及上述算法的局限性，本文提出一种多种群遗传算法(Multiple Population Genetic Algorithm，MPGA)，采用整数编码和自适应遗传算子，对各种群间进行协同优化，得到最优解。通过文献实例和实际应用验证算法的有效性。

1 路径柔性车间调度模型

假设有n个工件分配至m台设备上加工，每个工件i(i =1，…，n)有pi道工序{pi1，pi2，…pini}，工序pik的机器选择集为mik(mik⊆m)。pik在mj(mj⊆mjk)上的加工时间为Tikj，Tsikj为工序pik在mj开始时间，Te ikj为工序pik在mj的完工时间。工件i最后一道工序的完成时间Ci。Ci通常指工件的最短完工时间为性能指标，即:

模型需满足条件如下:①每个工件包含多个工序且工序按事先确定顺序加工;②一台机器同一时刻仅能加工一个工件;③一个工序一旦开始加工不得中断;④所有工件具有相同的加工优先级。

2 多种群遗传算法的设计

多种群遗传算法(MPGA)以标准遗传算法(Standard Genetic Algorithm ，SGA)为基础，通过对多个种群赋予不同的控制参数及移民算子［8］对种群间的协同进化，普通种群之间相互引入最优个体，最终构成精华种群。文中采用自适应交叉、变异概率，保证各种群得到实时有效的控制参数。

2.1 遗传基因编码

合适的编码是遗传算法的首要和关键问题，且编码需满足健全性、完备性和非冗余性三准则。路径柔性的JSP 问题比一般的JSP 问题复杂，常用两层编码［6］、基于工序的编码和机器的编码［7］等方式编码。本文采用整数编码方式，前半部分为工件加工顺序，后半部分为工序相应的加工机器序号。例如:

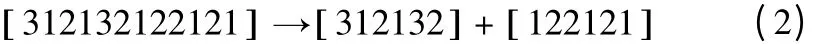
即工件加工顺序:工件3 的第一道工序→工件1的第一道工序→工件2 的第一道工序→工件1 的第二道工序→工件3 的第二道工序→工件2 的第二道工序。

对应的加工机器顺序:机器1→机器2→机器2→机器1→机器2→机器1。

2.2 选择算子(Genetic Operator)

选择算子通常采用轮盘赌法，该方法需对目标值与适应度值进行转换，但转换参数选取对优化结果有较大的影响。本文采用锦标赛法［9］，即随机选择三个个体，将最优的个体放入交叉池，其他个体返回种群重新参与选择。其目标值即适应度值，不必转换，以避免控制参数对结果的影响。

2.3 交叉算子(Crossover Operator)

交叉运算作是产生新个体的主要方法，提高全局搜索能力。对染色体的加工顺序部分进行单点顺序交叉，将交叉后工件多余的工序替换为其他工件的缺失工序;加工机器部分按交叉前个体所用的机器进行相应调整以保证其子代染色体的合法性。文中使用自适应交叉算子，其交叉概率PX为:

其中f为当前个体适应度值，favg为当前代个体平均适应度值，fmax为当前代个体最大值。

2.4 变异算子(Mutation Operator)

变异操作改善SGA 局部搜索能力，维持种群多样性。本文采用互换方式，对染色体中加工顺序部分随机选择两个变异位置，然后将两位置互换，同时加工机器号也随之对换。对换位置的加工机器号可由工序的机器集中随机选择与当前值不同的机器号代替。文中变异概率PM为:

2.5 算法流程图

图1 多种群算法的流程图

MPGA 算法是通过多个种群对解空间同时进行协调搜索，同时使用自适应交叉算子和变异算子对控制参数实时调整，以保证算法的局部和全局搜索，提高解的优化质量。本文以最大遗传代数为终止条件。其算法流程图如图1 所示。

3 仿真实例与应用

3.1 仿真实例

为验证该算法的性能，本文用Matlab7.9(2009b)软件编程，借用文献［1］、文献［3］及文献［10］实例进行多次实验对比分析。

文献［1］有6 个工件，每个工件6 道工序，在10 台机器上加工，即6 ×6 ×10 调度问题，其甘特图别如图2 所示:

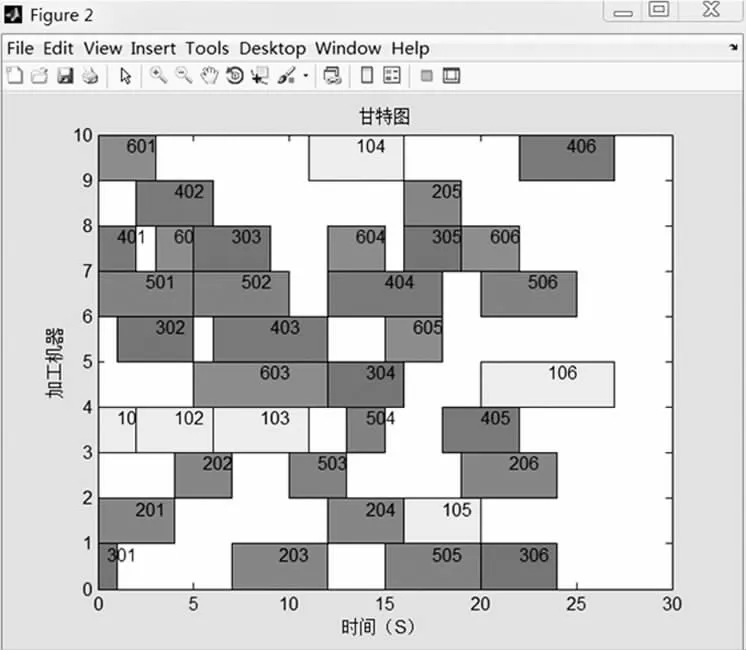
图2 6 ×6 ×10 调度甘特图

文献［10］有5 个工件，每个工件4 道工序，在6 台机器上加工，即5 ×4 ×6 调度问题，其机器甘特图如图3 所示。

图3 5 ×4 ×6 调度问题

利用MPGA 算法分别对文献［1］、文献［3］和文献［10］的案例进行仿真，算法运行30 次时的最优解、最差解及平均解如表1 所示。

表1 算法的比较结果

表1 可见，MPGA 算法明显优于文献［1］和文献［10］的算法，且与文献［3］取得相同的最优值。故MPGA 算法具有良好的可行性。

3.2 实例应用

某作业车间可以加工车、铣、刨、磨等，同时存在多个并行机和加工中心，属于柔性作业车间的范畴。现考虑一个10 台机床，6 个件且每个工件均为6 道工序的实际问题。工序可选择的机器如表2 所示，工序在机器的加工时间如表3 所示。

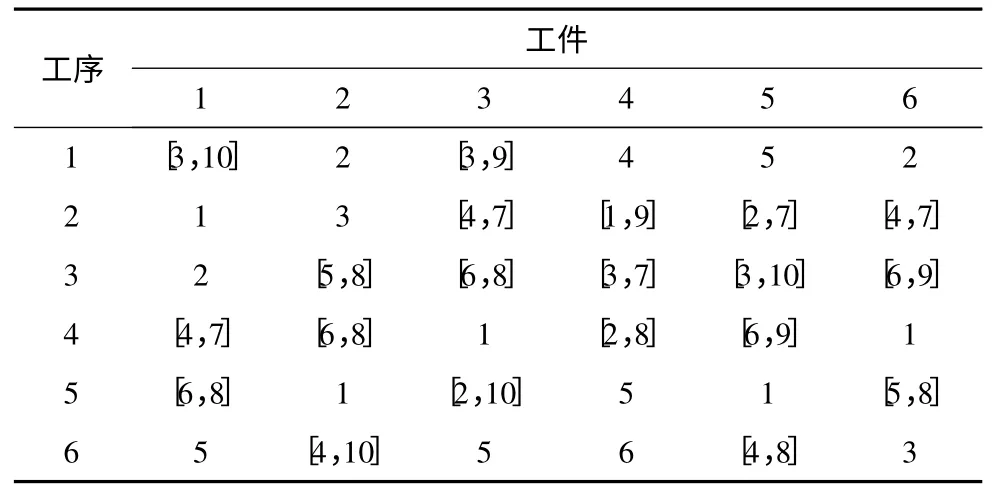
表2 工序可选择的机器

表3 工序在机器的加工时间表

其中，机床号1、2 车床;3、4 为铣床;5 为刨床;6为磨床;7、8 为钻床;9 为镗床;10 为加工中心。

规定种群规模为40，遗传代数300。应用MPGA算法搜索过程如图4 所示，调度甘特图如图5 所示。

图4 MPGA 算法的搜索过程

图4 表示MPGA 算法可迅速收敛到最优解，且均值变化比较平稳，可靠性高。验证了MPGA 算法优良的寻优能力，提高优化效率。

图5 MPGA 算法的调度甘特图

图5 表示各工件已被均匀合理的分配到可选择的加工机器上，且同一工件前后工序的衔接比较紧凑，如工件2、3、6 各工序的等待时间均为0。MPGA 算法获得全部工件的最短完工时间C =40 s，加工工序得到优化，有效地解决了实际调度系统中的路径柔性车间调度问题。

4 结论

针对路径柔性的作业车间调度问题，提出MPGA算法，将其与文献［1］、文献［3］及文献［10］案例进行仿真实验和对比，该算法避免了早熟收敛，提高优化效率，证实了该算法具有良好的可行性;仿真实例的实际应用，进一步证实了该算法的有效性和实用性。因此，MPGA 是路径柔性作业车间调度问题的可行、高效的算法，适合于复杂问题的求解优化，值得推广。

［1］邵斌彬，蔡鸿明，姜丽红. 一种柔性车间快速启发式调度算法［J］. 计算机应用与软件，2009，26(3):32 -34.

［2］贺仁杰，陈宇宁，姚锋，等. 求解柔性车间作业调度的知识型协同演化方法［J］. 计算机集成制造系统，2011，17(2):310 -315.

［3］王万良，赵澄，熊婧，等. 基于改进蚁群算法的柔性作业车间调度问题的求解方法［J］. 系统仿真学报，2008，20(16):4326 -4329.

［4］Seyed Habib A. Rahmati，M. Zandieh.A new biogeographybased optimization (BBO)algorithm for the flexible job shop scheduling problem［J］. Int J Adv Manuf Technol，2012，58:1115 -1129.

［5］F. Pezzella，G. Morganti，G. Ciaschetti. A Genetic Algorithm for the Flexible Job-shop Scheduling Problem［J］. Computers＆ Operations Research，2008，35:3202 -3212.

［6］余琦玮，赵亮，潘双夏. 基于遗传算法的柔性作业车间调度优化［J］. 组合机床与自动化加工技术，2004(4):32 -34.

［7］张超勇，饶运清，李培根，等. 柔性作业车间调度问题的两级遗传算法［J］. 机械工程学报，2007，43(4):119 -124.

［8］叶在福，单渊达. 基于多种群遗传算法的输电系统扩展规划［J］. 电力系统自动化，2000，24(5):24 -27.

［9］张国辉，高亮，李培根，等.改进遗传算法求解柔性作业车间调度问题［J］. 机械工程学报，2009，45(7):145-151.

［10］柳毅，马慧民，叶春明. 免疫遗传算法在柔性Job shop调度问题中的应用［J］. 上海理工大学学报，2005，27(5):393 -396.