中央子午线在机场建设中对跑道真方位的影响
2014-06-28朱晓江
朱晓江
(1.新疆水利水电勘测设计研究院测绘工程院,新疆 昌吉市 831100;2.武汉大学测绘学院,湖北 武汉 430079)
1 引 言
机场建设过程中,跑道设计使用的是真方位角,地形测绘使用的是坐标方位角。由于真方位与坐标方位使用的方向基准不同,且地形图又是机场建设技术设计所必须的基础资料,为了解决两个方向基准不同带来的误差有两个解决办法。第一,跑道设计改正方法。按常规地形测量进行作业,提交地形测量图纸成果,在地形图上设计跑道前先计算坐标方位角与真方位角的差值,如果差值很小(跑道中心离中央子午线距离很近),可直接在地形图上进行设计;如果差值很大,在设计时加上这个差值进行改正,以保证跑道实地放样后的真方位与设计真方位最大限度地接近。但是使用该方法对设计方技术人员的测绘专业基础要求高,不推荐使用。
第二:使用跑道中心或跑道中心附近的经度作为中央子午线,建立相对独立平面坐标系,开展地形测绘工作,将地形测绘成果提交设计单位进行方位设计,在设计基础(地形图)上减小两者的差值,方便设计与后续施工。
2 中央子午线与真方位角
机场跑道方位设计使用的方向基准为真北方向,即真子午线方向。机场地形测绘使用的方向基准为坐标北方向,即与平面坐标系中央子午线平行。除了上述真北方向和坐标北方向外,还有以磁子午线为方向基准的磁北方向。常用的三北关系[2],如图1 所示。
机场地形测绘时,会根据测区的地理位置计算长度投影变形值,按《工程测量规范》变形值大于2.5 cm/km时[1],需建立相对独立坐标系以减小偏离中央子午线和高程投影带来的长度投影变形值。当机场跑道中心偏离3°带中央子午线较近时,可考虑直接使用中3°带中央子午线,边长投影至测区平均高程面来建立相对独立坐标系;当机场跑道中心偏离3°带中央子午线较远时,经常使用的方法是:选择跑道中心的经度或跑道中心附近某一点的经度作为相对独立平面坐标系的中央子午线,边长投影至测区平均高程面来建立相对独立坐标系。建立好的平面坐标系方向基准为坐标北方向,即高斯投影时投影带的中央子午线的方向,这也意味着地形图上任意一点的北方向与坐标系选择中央子午线平行。
由图1 可知地面上两点的真方位角与坐标方位角并不相等,真方位角与坐标方位角做近似转换时可不用考虑这两点的大地线高斯投影的方向改化,加上子午线收敛角的改正即可相互转换计算[2]。坐标方位角与真方位角的关系如图2 所示。
两者转换的严密计算方法[3,4]是:

式(1)中,APQ为PQ 的真方位角,αPQ为PQ 的坐标方位角,γP为经过P 点的子午线收敛角,δPQ为方向改化。
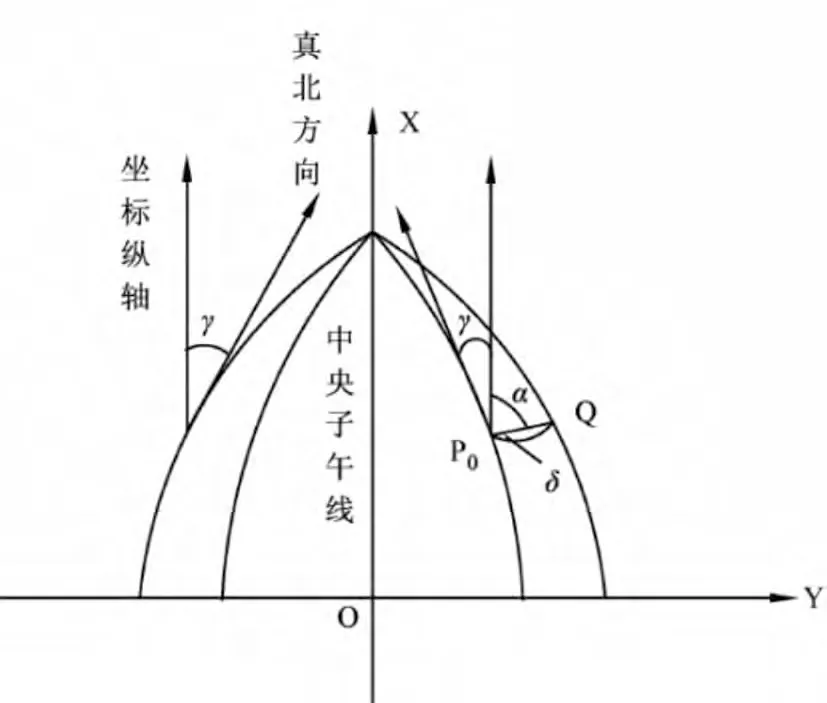
图2 真方位角与坐标方位角示意图
高斯投影时,若纬度保持不变,偏离中央子午线越远,子午线收敛角越大,长度变形也越大[2]。由式(1)可知,子午线收敛角越大,地面两点的真方位角与坐标方位角之间的差值也越大。为使得两者的差值尽可能小,机场地形测绘项目技术设计时必须考虑地形测绘对长度变形的要求和机场跑道真方位设计的精准度。对于机场而言,机场跑道的长度一般不大于3 km,范围很小,方向改化值对真方位角计算的结果影响不显著。地形测绘建立平面坐标系,选择的中央子午线位于跑道中心时,跑道两端的子午线收敛角的绝对值近似,符号相反,跑道两端的正反真方位角的差值也接近180°;同时跑道两端的真方位角与坐标方位角的差值最小,机场跑道的真方位设计精准度也最高。所以,选择的中央子午线离跑道中心越近,真方位角与坐标方位角的差值也越小,跑道真方位设计的精准度也越高。
3 工程实例
(1)机场概况
位于新疆的某机场,已知跑道中心的大地坐标(1980 西安坐标系),跑道真方位120°~300°,跑道全长2 600 m,跑道中心经度为89°30'39.06″,3°带中央子午线为90°,平面坐标系基准为1980 西安坐标系。机场地形测绘时,布设有二等控制网(平面等级为二等,高程等级为相对独立的二等),控制点(以下称测图控制点)均匀分布于机场跑道及其他机场建筑物外围,地形测绘比例尺1∶2 000。
(2)作业方法与计算过程
平面控制测量联测3 个国家二等三角点(成果为1980 西安坐标系),将布设的测图控制点与这三个三角点一起组网,使用GPS 相对静态定位测量方法观测,使用Cosa GPS 数据处理软件进行控制网平差计算。在判断已知点稳定、成果可靠后,使用这3 个点的成果约束平差得到测图控制点在1980 西安坐标系3°带高斯平面直角坐标系下的平面坐标;对测图控制点成果进行换带计算(由中央子午线90°换带至89°31')得到测图控制点任意带(89°31')高斯平面直角坐标,使用接近跑道中心的控制点“XX”的任意带高斯平面直角坐标和该点至另一控制点“XX”的坐标方位角(使用这两点的任意带高斯平面直角坐标反算得到)为起算数据,用Cosa GPS 数据处理软件“一点一方向”平差,边长投影至测区平均高程面(935 m),建立测区相对独立坐标系,得到测图控制点在独立坐标系下的平面坐标,使用测图控制点的相对独立坐标系成果进行地形测绘。机场跑道与中央子午线相对关系如图3 所示:

图3 机场跑道与中央子午线
高程控制由国家二等水准点起测,联测布设的所有控制点,组成闭合水准路线,按二等水准测量方法观测;使用水准平差程序进行平差计算得到测图控制点的高程。
(3)结果说明及真方位计算
设计单位根据1∶2 000地形图进行工程平面图设计,使用GPS RTK 根据工程平面图放样并测量得到跑道两端和跑道中心的相对独立坐标系平面坐标,使用高斯反算程序计算得到跑道两端(西端W,东端E)的大地经纬度(1980 西安坐标系)和子午线收敛角。结果如表1 所示。

跑道端点子午线收敛角 表1
由式(1)可知,坐标方位角可根据平面坐标计算得到,待求得方向改化值[5],代入式(1)计算,即得到跑道的真方位角。以图2 为例:
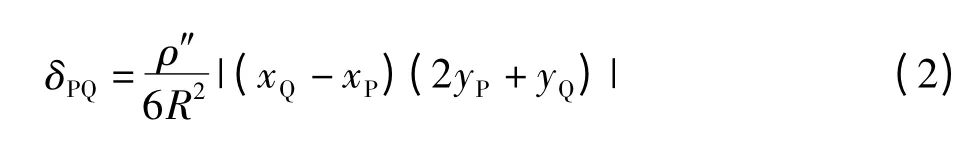
式(2)计算得到的只是方向改正的绝对值,实际上由于大地线的位置与方向不同,δ 的数值可能为正也可能为负,这里由于跑道两个端点分布在中央子午线两侧(如图3 所示),计算方向改化值时要根据中央子午线分成两段,并分别计算,即δWE的符号为正,δEW的符号也为正。经计算,结果如表2、表3 所示:

机场跑道WE 的方位角 表2

机场跑道EW 的方位角 表3
表2与表3中的δWE、δEW的计算值分别为0.002 4″、0.000 5″,式(2)的计算误差可精确至0.01″,从结果可以看出,方向改化对真方位角计算结果影响不显著。跑道真方位误差取决于子午线收敛角的大小,最大差值为-54″,误差在1'以内。
(4)模拟计算
根据跑道中心的大地坐标(纬度,经度)、1∶10 000地形图资料(中央子午线90°)和跑道长度方位模拟出一个机场跑道(西端W'、东端E',位于中央子午线东侧),并根据两端点平面坐标计算坐标方位角,子午线收敛角和方向改化,最终计算得到真方位误差,模拟计算结果如表4、表5 所示:

机场跑道W'E'的方位角 表4

机场跑道E'W'的方位角 表5
表4、表5 计算结果可以反映出,方向改化误差对真方位影响很小,真方位误差近似等于子午线收敛角,最大差值为-22'02.58″,误差较大。
4 结 语
目前,没有机场建设工程相关的测量规范依据,在这种前提下,以满足工程施工及运行使用为条件,要求方向基准带来的误差越小越好。通过工程实例,地形测绘选择跑道中心附近经度的作为中央子午线建立相对独立坐标系,这样就能使得跑道两端的子午线收敛角减小,从而使得真方位角与坐标方位角的差值减小,地形图成果可以直接供设计方使用。
使用这种方法从根本上一次性解决两个方向基准不同带来的误差对机场跑道建设的影响,对今后机场建设工程有很强的借鉴意义,并且适用于同类涉及真方位的工程建筑。
[1]GB50026-2007.工程测量规范[S].
[2]潘正风,程效军,成枢等.数字测图原理与方法(第二版)[M].武汉:武汉大学出版社,2009.
[3]季凯敏,王解先.利用大地坐标计算真方位角的两种方法[J].工程勘察,2009(4):84~86.
[4]孔祥元,郭际明,刘宗泉.大地测量学基础(第二版)[M].武汉:武汉大学出版社,2010.
[5]田青文,刘万林.控制测量学[M].西安:西安地图出版社,2004.
