利用测井、压裂资料求取储层地应力的方法

2014-06-28杨红许亮何衡梁峰王京舰于海棠

断块油气田 2014年4期

杨红，许亮，何衡，梁峰，王京舰，于海棠

（1.延长油田股份有限公司开发部，陕西延安 716000；2.中国石油长庆油田公司油气工艺研究院，陕西西安 710018；3.延长油田吴起采油厂，陕西吴起 717600；4.中国石油长庆油田公司勘探开发研究院，陕西西安 710018）

存在于地壳内的应力统称为地应力，是由于上覆岩层重力、地壳内部的垂直运动和水平运动及其他因素综合作用引起内部单位面积上的作用力。地层破裂压力定义为使地层产生水力裂缝或张开原有裂缝时的井底流体压力。地应力和破裂压力是钻井、增产改造、防砂、注水等作业方案设计的基础数据。采用压裂法求取地应力和破裂压力准确，但资料不够充分也不连续，采用测井法资料丰富、经济、可靠且连续；因此，将测井资料和压裂资料结合起来求取地应力和储层破裂压力，是既方便又准确的首选方法。

1 储层岩石力学参数计算

1.1 声波时差获取

纵、横波时差是计算地层岩石力学参数必须的声波测井资料，可以从全波列测井资料中提取，但多数井仅有常规纵波测井资料，因此，需利用常规纵波时差求取横波时差值［1］。

1）Cristensen 法。

砂岩：

泥岩：

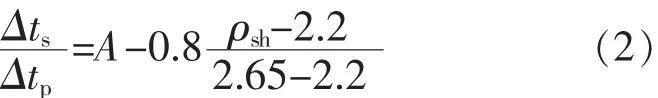
其中：A=2.5 g/cm3，ρsh≤2.2 g/cm3；A=2.5 g/cm3，ρsh≥2.65 g/cm3。

2）砂岩或泥质砂岩地层估算横波时差：

X，Y，Z是经验常数，不同的油区有所不同，通常取值为：X=2.121 5，Y=45.328 7，Z=-167.312。

1.2 岩石动态参数计算

目前岩石力学参数的测定方法包括动态法和静态法。动态法是通过测定声波在岩样中的传播速度转换得到动态力学参数；静态法是对岩样进行加载测其变形得到静态力学参数。由于静态参数的测定所需代价和成本太高且不连续，因此在工程上常使用动态法进行动态力学参数测定。

利用声波时差值和密度测井值，便可以计算岩石的动态力学参数［2-3］。

1）动态泊松比：

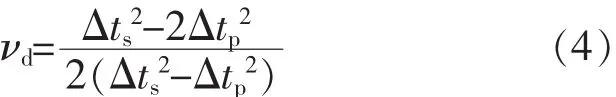
2）动态弹性模量：

3）动态体积模量：

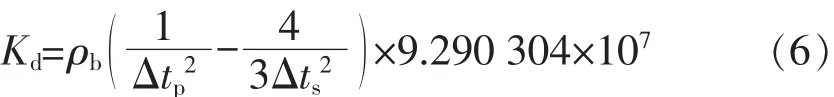
4）体积压缩系数：

5）骨架压缩系数：

6）Biot弹性系数：

7）抗张强度：

当地层骨架不含放射性矿物时，地层的自然放射性强度主要取决于地层中的泥质体积分数。在这种条件下，可以利用自然伽马测井资料按式（10）计算泥质体积分数Vsh。

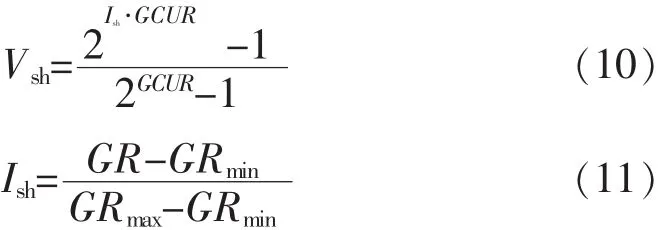
Deere 和 Miller［4］在实验基础上，得出岩石单轴抗压强度Sc与岩石弹性模量E和泥质体积分数Vsh之间的关系。

砂岩：

碳酸盐岩：

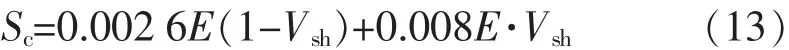
Coates［5］等人提出了抗张强度（St）与 Sc的关系。

岩石有天然裂缝时：

岩石无天然裂缝时：

1.3 岩石静态参数计算

因地下岩层的应力形成、赋存和起作用的机理，特别在应力幅值、加载速度和所引起的岩石变形等方面，更接近岩石静态测试的条件，故在地应力计算和实际工程中应采用岩石的静态力学参数。因此，必须研究动静态参数转换关系，以计算岩石静态力学参数［6-8］。

本文通过对某断块测井计算所得岩石动态力学参数和岩心实验所得岩石静态力学参数进行线性拟合，得出动静态弹性模量和泊松比之间的转换关系为

2 地应力与破裂压力计算

2.1 地应力计算

实际中，常用分段求和的方法进行计算：

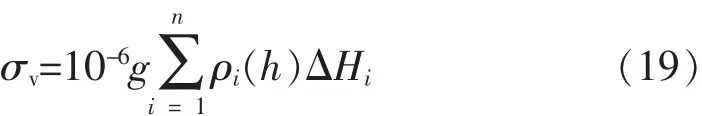
垂向应力即上覆岩层重力为

本文在储层均质、各向同性和弹性变形的假定下，考虑水平方向构造应力不等，结合Biot有效应力推导得出的黄荣樽模型［9］为

2.2 构造应力系数计算

由水力压裂施工曲线（见图 1）［10］可看出：

不考虑滤失时

考虑滤失时

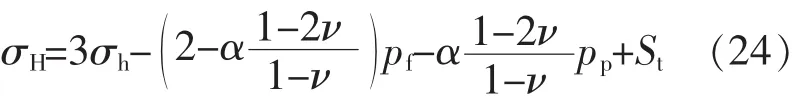
由式（22）—（24）可求出最小水平主应力 σh和最大水平主应力σH，将测井资料计算所得岩石力学参数，代入式（20）和（21），即可反算出最小和最大水平主应力方向的地质构造应力系数β和γ。

图1 水力压裂施工曲线

2.3 破裂压力计算

本文使用模型为王鸿勋模型［10］，属于H-F模式，不考虑滤失时简化为H-W模式。在储层均质、各向同性和弹性形变的假定下，考虑了井眼应力集中、水平主应力不等、压裂液向地层内渗滤的影响，结合Boit有效应力原理推导得出：

考虑滤失时（针对渗透性地层）为

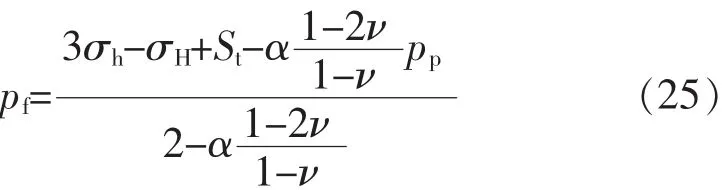
不考虑滤失时（针对非渗透性地层）为

3 模型应用与验证

将上述方法通过VB6.0语言编程，实现应用测井、压裂资料进行地应力和破裂压力计算的快速处理［11-18］。利用该程序对×井3 590～3 920 m层段进行了实例分析，其中压裂层段为3 724～3 785 m。

3.1 地层构造应力系数计算

研究区×井邻井的压裂层段破裂压力为86.819 MPa，闭合压力为75.819 MPa，地层压力为49.450 MPa，抗张强度为 16.333 MPa。由式（22）和（24）得出最小、最大水平主应力分别为75.819 MPa和83.295 MPa，进而计算出构造应力系数分别为0.462和0.586。

3.2 地应力和破裂压力计算

获得区块构造应力系数后，利用×井声波时差、密度、自然伽马测井资料，即可计算出3 590～3 920 m层段的岩石力学参数、三向地应力和破裂压力［17-22］（见图 2）。

研究层段的岩石力学参数结果见表1。垂向应力为82.245～91.873 MPa，最小水平主应力为62.417～84.565 MPa，最大水平主应力为67.651～94.474 MPa，破裂压力为75.346～93.241 MPa。水平主应力和破裂压力随深度增加总体趋势不断增大，但在3 615～3 640 m随深度增加有所下降，是由于此段砾岩体积分数小（2.7%），页岩体积分数高（37.6%），密度较低（2.2～2.3 g/cm3）。

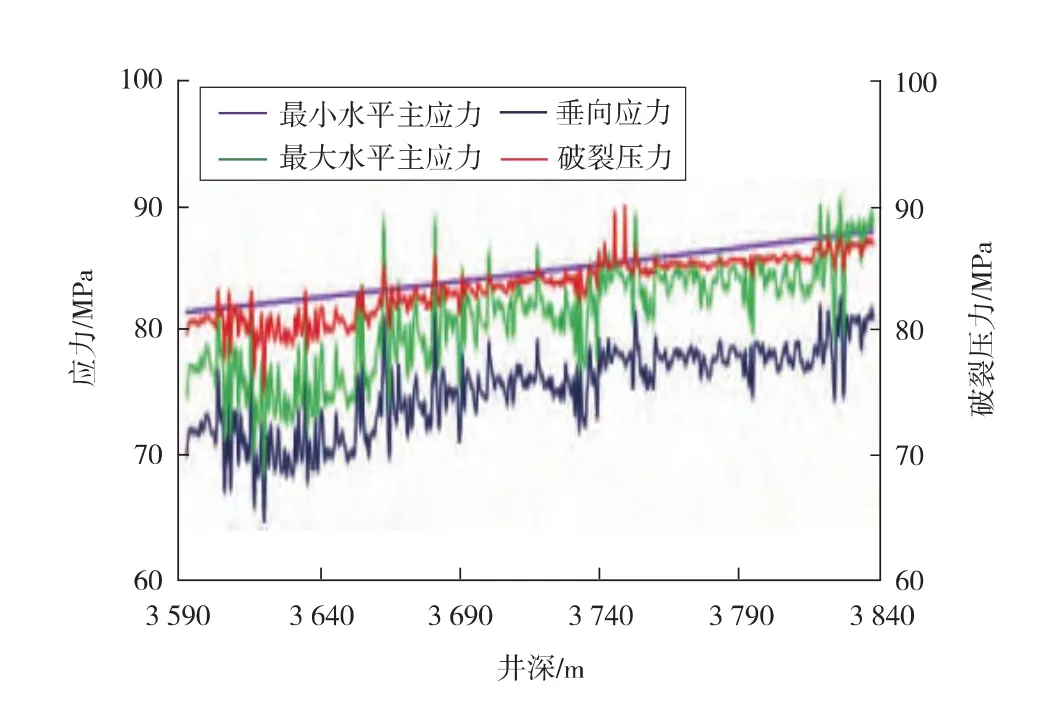
图2 三向地应力和破裂压力剖面

表1 研究层段岩石力学参数

4 结论

1）岩石力学参数与声波纵、横波速和地层密度密切相关，利用声波时差、密度和自然伽马测井资料能得到岩石力学参数连续剖面。

2）岩石动、静态参数间有一定经验关系，可利用测井计算结果与室内岩心实验结果拟合线性关系式。

3）利用测井资料结合压裂资料计算地应力和破裂压力简便且准确，是地应力计算的首选方法。

5 符号注释

Δts，Δtp分别为地层横波、纵波时差，μs/ft；Δtmas，Δtmap分别为地层骨架的横波、纵波时差，μs/ft（1 ft=0.304 8 m)；Δtfs，Δtfp分别为地层流体的横波、纵波时差，μs/ft；A 为砂岩岩石密度，g/cm3；ρsh为泥岩的体积密度，g/cm3；ρ为密度测井值，g/cm3；ρma为地层骨架密度，g/cm3；νd为动态泊松比，无因次；νs为静态泊松比，无因次；Ed为动态弹性模量，MPa；Es为静态弹性模量，MPa；E 为弹性模量，MPa；Kd为动态体积模量，MPa；G为剪切模量，MPa；Cb为岩石体积压缩系数，MPa-1；Cma为岩石骨架压缩系数，MPa-1；α为Boit系数；Vsh为泥质体积分数，无因次；Sc为单轴抗压强度，MPa；St为抗张强度，MPa;GR为目的层GR值，API；GRmin为纯砂岩层段 GR 值，API；GRmax为纯泥岩层段 GR 值，API；Ish为泥质指数，无因次；GCUR为经验指数，对新地层取3.7，老地层取 2；ν为泊松比，无因次；σv为深度 h 处的垂向应力，MPa；ρ（h）为随深度变化的上覆岩体密度，kg/m3；h为地层层位深度，m；σh为最小水平主应力，MPa；σH为最大水平主应力，MPa；pp为孔隙压力，MPa；β为最小水平主应力方向上的构造应力系数，无因次；γ为最大水平主应力方向上的构造应力系数，无因次；ps为瞬时停泵压力，MPa；pf为破裂压力，MPa；σt抗张强度，MPa；pr是重张压力，MPa；Pc是裂缝延伸压力，MPa。

［1］张敏.基于声波测井信息的地应力分析与裂缝预测研究［D］.东营：中国石油大学，2008.

［2］刘向君，刘堂晏，刘诗琼.测井原理与工程应用［M］.北京：石油工业出版社，2006：106-118.

［3］张筠，林绍文.利用测井进行地层弹性特征及应力场分析［J］.测井技术，2001，25（6）：467-472.

［4］Deere D U，Miller R P.Engineering classification and index properties for intact rock ［R］.Kirtland Base:U S Air force Weapons Laboratory,Technical Report AFWL-TR-65-116，1966.

［5］Coates G R，Denoo S A.Mechanical properties program using Borehole analysis and Mohr′s Circle［R］.Houston:Twenty-Second Annual Logging Symposiums Transactions，1981.

［6］Kuhlman R D.Field tests of downhole extensometer used to obtain insitu stress data［R］.SPE 25905，1993.

［7］Myung J I，Helander D P.Correlation of elastic modulus dynamically measured by in-situ and laboratory techniques［R］.Houston：Thirteen Annual Logging Symposium Transactions，1972.

［8］Eissa E A,Kazi A.Relation between static and dynamic Young′s Modular of rocks［J］.International Journal of Rock Mechanics and Mining Science&Geomechanical Abstracts，1988，25(6):479-482.

［9］黄荣樽.地层破裂压力预测模式的探讨［J］.华东石油学院学报，1984，26（4）：335-347.

［10］李颖川.采油工程［M］.北京：石油工业出版社，2009：202-207.

［11］王鸿勋.水力压裂原理［M］.北京：石油工业出版社，1987：1-6.

［12］周拿云，杨兆中.地层破裂压力预测技术综述［J］.重庆科技学院学报：自然科学版，2011，1（13）：36-39.

［13］许风光，陈明，高伟义.利用测井资料分析计算东海平湖油气田地应力［J］.断块油气田，2012，19（3）：401-405.

［14］董光，邓金根，朱海燕，等.重复压裂前的地应力场分析［J］.断块油气田，2012，19（4）：485-488，492.

［15］孙峰，李行船，熊廷松，等.低渗透油藏水力压裂井应力场转向定量评价［J］.断块油气田，2012，19（4）：489-492.

［16］冯青，刘启国，李海旭，等.渗透率应力敏感效应对气水井产能的影响［J］.断块油气田，2013，20（1）：89-91.

［17］潘伟义，伦增珉，王卫红，等.异常高压气藏应力敏感性实验研究［J］.石油实验地质，2011，33（2）：212-214.

［18］张奉东，马收.松辽盆地长岭凹陷腰英台油田地应力及天然裂缝场研究［J］.石油实验地质，2008，30（2）：150-153.

［19］佟彦明，钟巧霞.利用平衡剖面快速判定盆地区域古构造应力方向：一种分析古构造应力方向的新方法［J］.石油实验地质，2007，29（6）：633-636.

［20］杨少春，郭智，刘金华，等.商741火成岩区构造应力场模拟及裂缝预测［J］.断块油气田，2011，18（3）：277-280.