关于保守力判断的数学形式
2014-06-28刘红梅
刘红梅 汪 瑜 徐 莹
(空军航空大学基础部 吉林 长春 130022)
对于保守力的概念,在书中基本上都是从讨论重力、万有引力、弹簧弹力做功角度出发,观察共同特点得出两种表述方式:一种是做功只与始、末位置有关,与质点经历的路径无关,把具有这种做功性质的力称为保守力;另一种表述即质点沿任意闭合路径运动一周,保守力对它所做的功为零,数学表达式
A=∮lF·dl=0
课本上这样讲解之后,学生并不能真正理解什么样的力是保守力,只能片面地记住以上3种力是保守力,并且别人问为什么时,只把前面概念重复一下,对于保守力并没有深刻的认识.本文从力的数学表达式出发,把抽象的保守力概念形象起来.
先来看几个力的表达式,为方便我们把它们用直角坐标表示出来,判断这几个力中哪些是保守力,如:(1)F=(4-2y)i;(2)F=yi+yj;(3)F=3.5x2+x+5;(4)F=x2i+yj;(5)F=2i-yj+2zk.在这几个力中(1)、(2)是非保守力,(3)、(4)、(5)是保守力.在文献[1]中有一道让学生认识功是过程量的实例,我们从此实例出发,归纳其中的特点.
【例题】[1]一质点沿如图1所示的路径运动,求力F=(4-2y)i(SI)对该质点所做的功:
(1)沿ODC;(2)沿OBC.

图1
解析:(1)质点沿ODC从O运动到C
由题意知Fx=4-2y,Fy=Fz=0,在O到D的路径上,y=0,x从零变到2 m;在D到C的路径上,力F与路径垂直而不做功.因此,F所做的功为
(2)质点沿OBC从O运动到C
同理,在O到B的路径上力F与路径垂直而不做功;在B到C的路径上y=2 m,x从零变到2 m.因此,F所做的功为

可见此力做功与路径有关,力F=(4-2y)i为非保守力.
依照上题的解法,如果力的表达式变化了,读者可以自行证明上述5个力的表达式中,哪些力做功与路径无关,哪些有关,可以清楚地看出之前结论的正确性.
下面我们总结一下,如何从数学表达式上来看一个力是不是保守力.理论很简单,来源于功的定义:力所做的功(含义1)等于力与力方向上位移的乘积.想让力所做的功与路径无关只与始末位置有关,只需要这个力在任一方向上的分量满足一个条件,即如果力在某一方向上的分量是某一变量的函数,则要求这一变量必须为此方向变量,比如上述5个力表达式中(3)、(4)、(5)在x轴上的分量分别为变量3.5x2+x+5,x2和常量2,均为x的变量;在y轴上的分量分别为常量零和变量y,-y,均为y的变量;在z轴上的分量分别为常量零,零和变量2z,均为z的变量,所以保守力的函数应为
F=f(x)i+f(y)j+f(z)k
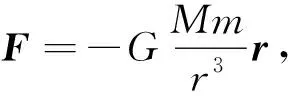
以上结论可以加强学生对保守力的认识,更好地理解什么样的力做功与路径无关,保守力的特性如何在坐标系中体现出来,更直观、形象.但我们也要清醒地认识到这一结论仅是保守力的充分条件,并不是所有的保守力都能写成上述形式.
参考文献
1 康颖. 大学物理(第二版).北京:科学出版社,2010 . 54~55
