透镜加速运动时像的运动规律的探讨

王云创 刘俊杰 邢 娟

(滨州医学院物理学教研室 山东 烟台 264003)

1 引言

在凸透镜成像过程中，物距、像距之间的变化关系受透镜成像高斯公式[1～3]的约束，调节透镜成像时，透镜和像的速度之间保持一个动态的关联关系[4～6].若物固定不动而透镜沿主光轴做匀加速直线运动时，像也必然随着透镜做相应的运动，那么像的速度和加速度随时间的变化规律如何？下面将推导这种变化规律的函数关系式，并且结合绘制的函数关系曲线对其物理意义进行分析探讨.

2 公式的导出

建立如图1所示的坐标系.

图1 成像光路图

物P固定于坐标原点O处，物经凸透镜成像P1.设x为物距即透镜L的位置坐标，s(x)为像的位置坐标，则像距为s(x)-x.令透镜自x=x0>f处(成实像)以恒定加速度a0沿x轴正方向做初速度为零的匀加速直线运动.显然，透镜的速度为v0(t)=a0t，物距为

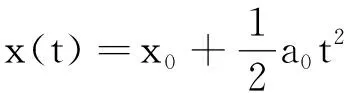
据薄透镜成像公式

整理可得像的位置坐标为

(1)

对式(1)分别求一阶和二阶导数，可得像的速度v(t)和加速度a(t)的表达式为

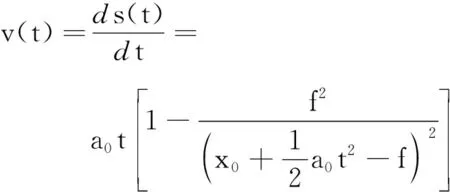
(2)

(3)

为了能定量地看出v(t)、a(t)随t的变化规律，不妨取a0=5 cm/s2，x0=20 cm，f=15 cm，分别代入式(2)、(3)，绘得像的速度v(t)和加速度a(t)随时间t的变化规律曲线，如图2，3所示.从图2,3 可见，速度v(t)和加速度a(t)的大小和方向均随时间t发生变化，都有一个极值点，并且经过一定时间后速度v(t)与时间t成线性关系，而加速度a(t)趋向恒定值.

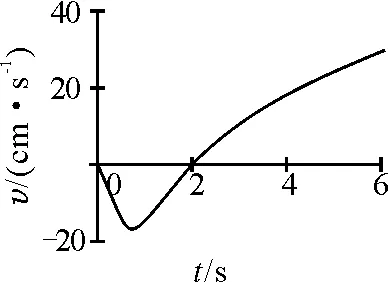
图2 v(t)-t曲线

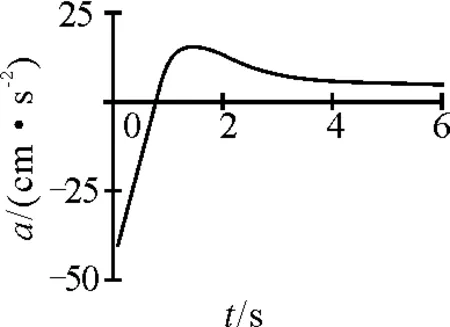
图3 a(t)-t曲线

3 分析讨论

3.1 像的速度v(t)的极值

为推导方便，令Δ=x0-f.对v(t)求导即利用式(3)令a(t)=0，整理可得

Δ(Δ2-f2)=0

令y=t2,代入上式整理得

令

代入上式整理得

则上述方程的有效解为

利用上述有关变换关系式可得

(4)

将式(4)代入式(2)可得速度极值的一般表达式，但公式太烦琐，此处仅以具体数据来验证，即将a0=5 cm/s2，x0=20 cm，f=15 cm，代入式(4)可得速度v(t)极值点处对应的时间的平方数值为

即

t2≈0.519 s2t≈0.720 s

将该时间值代入式(2)、(3)，可得像的速度极值和该时间对应的像的加速度值分别为v≈-16.834 cm/s和a=0，从图2,3也可看出.

3.2 像的加速度a(t)的极值

将式(3)求导并令其等于零，整理得像的加速度极值点处对应的时间为

或

(5)

将式(5)分别代入式(2)、(3)，可得加速度极值时对应的像的速度和加速度的一般式为

(6)

(7)

将a0=5 cm/s2，x0=20 cm，f=15 cm，代入式(5)、(6)、(7)，可得像的加速度a(t)的极值点对应的时间t2=2 s2，即t≈1.41 s，此时对应的加速度的极值为a=16.25 cm/s2，该时间对应的像的速度为v=-8.839 cm/s，从图2,3可看出这种对应关系.

3.3 像的速度和加速度的趋向值

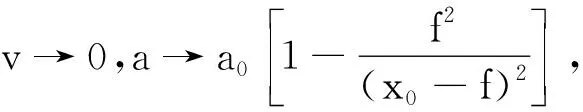
3.4 像的速度和加速度方向发生改变的转折点

对于速度v(t),令式(2)等于零可解得对应的两个时间为

取a0=5 cm/s2，x0=20 cm，f=15 cm，可得t=2 s.图2可见，tt2时，v(t)>0 ，即像的速度与透镜的速度方向相反；t>t2时，v(t)>0 ，即像的速度与透镜的速度方向相同.将t2代入物距公式，可得x=2f，说明像的速度方向发生改变的转折点在两倍焦距处.

对于加速度a(t),当

时，a(t)<0，即像的加速度与透镜的加速度方向相反.当时，a(t)>0，即像的加速度与透镜的加速度方向相同.

4 小结

由于物距和像距受到透镜成像公式的约束，或者说物和像的速度、加速度间的关系也必然相互制约，因此像的运动规律不但复杂且很难想象，通过上述公式描述、图形化处理以及关键点的分析，对像的运动规律给出了比较清晰的全貌情况，对于学生理解透镜成像规律具有一定的指导意义.

参考文献

1 程守洙，江之永．普通物理学(第三分册)(第五版)．北京：高等教育出版社，1999.168～277

2 王楚，唐浚雄．光学．北京：北京大学出版社，2001.252～262

3 梁绍荣，刘昌年，盛正华．普通物理学(第四分册) 光学(第二版)．北京：高等教育出版社，1994.30～67

4 黄勇．透镜成像中物像运动速度的相互关系．物理通报，1998(7)：20

5 齐景荣，曲红斌，雷桂林．对不同介质中的透镜成像时物、像运动规律的探讨．甘肃联合大学学报(自然科学版)，2005，19(3)：74～75

6 易志毅．物、像关系初探．广西物理，1994，15(5)：21～22