带电体低速运动时电磁场的能量和动量

苑新喜

[中国地质大学(武汉)数学与物理学院 湖北 武汉 430074]

1 均匀带电球面

依据电磁场的相对论变换，文献[1]已给出了以速率v匀速运动的均匀带电球面的电磁场能量

其中

c为真空中的光速，W0是带电球面静止时的电磁场能量.

随后，文献[2]又给出了该带电球面运动时的电磁场动量

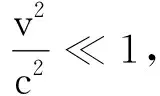
即得

仿照狭义相对论中质点的动能的定义[3]，此处尝试定义电磁场形式上的相对论动能为

Wk=W-W0

由此得到带电球面低速运动时电磁场形式上的动能

同时，对于动量，可取γ=1，即有

狭义相对论中静质量为m0的质点低速运动时动能和动量关系[3]

仿照于彼，此处尝试给出带电球面低速运动时电磁场形式上的动能和动量关系

2 通电螺绕环

其中W0是通电螺绕环静止时的电磁场能量.V′表示Σ′系中电磁场分布空间(下同).

同理

同理

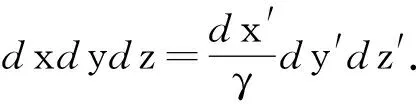
综上，沿垂直于环面方向运动的通电螺绕环的电磁场能量

易知，在Σ系中通电螺绕环的电磁场动量密度gEM=ε0E×B的各个直角分量

gx=ε0(EyBz-EzBy)≠0

gy=ε0(EzBx-ExBz)=0

gz=ε0(ExBy-EyBx)=0

又有

∭V(ε0EyBz)dxdydz=

(1)

同理

所以，沿垂直于环面方向运动的螺绕环的电磁场动量为

p=px=∭Vgxdxdydz=

同样类似于前面带电球面的近似运算，当通电螺绕环低速运动时，螺绕环的电磁场能量

形式上的动能

动量

此种情形下通电螺绕环低速运动时电磁场形式上的动能和动量关系为

3 圆柱形电容器

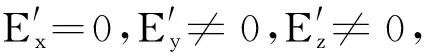
其中W0是该充电电容器静止时的电磁场能量.

同理

同理

综上，沿平行于轴向运动的充电圆柱形电容器的电磁场能量

易知，在Σ系中电容器的电磁场动量密度gEM=ε0E×B的各个直角分量

gx=ε0(EyBz-EzBy)

gy=gz=0

同时类比于前面式(1)有

∭Vε0EyBzdxdydz=

则沿平行于轴向运动的电容器的电磁场动量为

同样类似于前面带电球面的近似运算，当圆柱形电容器低速运动时，电容器的电磁场能量

形式上的动能

动量

此种情形下该电容器电磁场形式上的动能和动量关系为

4 平行板电容器

平行板电容器以速率v沿垂直于板面的方向运动时，只有垂直于板面的电场(即只有平行于运动方向的电场)，无磁场. 易知，该电磁场的能量为

动量

p=0

其中W0是该电容器静止时的电磁场能量(这个结论出乎意料，笔者认为这恰恰说明了电磁场这种物质形态的特殊性).

当平行板电容器低速运动时，电磁场能量

该电磁场形式上动能

参考文献

1 苑新喜. 均匀带电球面匀速运动时的电磁场能量. 中国基础科学, 2012， 14(6) :37～38

2 苑新喜. 带电球面运动时的电磁场动量. 物理通报，2013(11):19～21

3 张三慧. 大学物理学——力学(第二版). 北京：清华大学出版社, 1999.324，332

4 张三慧. 大学物理学——电磁学(第二版). 北京：清华大学出版社, 1999.261,142