向量问题的数形结合

杨具军

（浙江省温州市沙城高级中学，浙江 温州 325025）

向量问题的数形结合

杨具军

（浙江省温州市沙城高级中学，浙江 温州 325025）

向量既有数的特征，又有形的特点，堪称数形结合的经典，不少平面向量问题，运用代数法与几何法求解，可以极大地丰富学生的思维，开阔学生的视野，锻炼学生的解题能力。

向量问题；中学数学；平面向量问题

笔者就教学中遇到的几个问题摘录如下，供大家赏析.

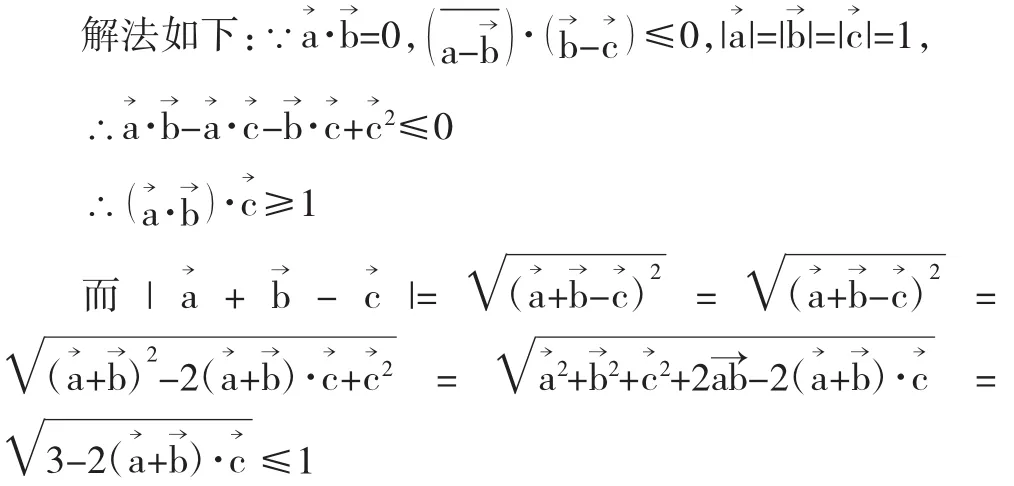
从而选B.

点评：直接从基本的代数运算入手，思路清晰，自然流畅。

点评：向量的线性运算，使形与数完美地结合，数形结合，使问题直观、形象、活生生地展现出来，体现了数学的神奇与美。

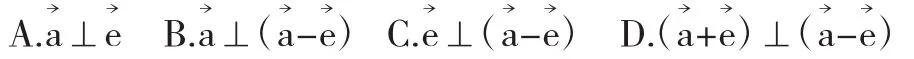
学生想法1：代数方法

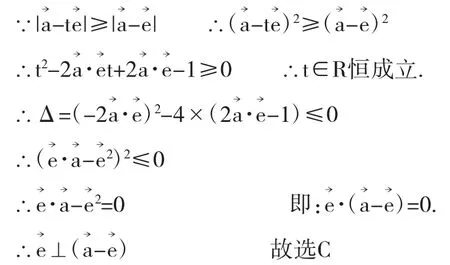
点评：基础知识扎实，基本功硬，不失为一种容易入手的好方法。

学生想法2：几何方法

点评：数形结合的引入使枯燥无味的数学充满了动感，同时也避免了繁杂的去处，数学的美不就在其中吗?

向量问题的代数运算可以有效考查学生的运算能力、变形能力，但对于解题来说，有时显得有点烦琐，几何方法不但可以化繁为简，更主要的是能有效地训练学生的思维，开阔学生的视野，增强学生学习数学的兴趣，提高解题效率，让学生陶醉于数形结合的优美境界.

巩固练习：

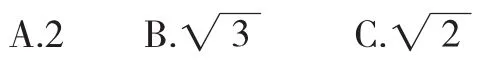
参考答案：

∴点M是△ABC的外接圆上的动点，显然AM为直径时最大，由正弦定理便可快速得到答案，故选A.

G633.6

A

1674-9324（2014）07-0251-02