定义域优先原则在解决函数问题中的应用

苏旭景

（河北枣强中学，河北 枣强 053100）

定义域优先原则在解决函数问题中的应用

苏旭景

（河北枣强中学，河北 枣强 053100）

函数的定义域具有不可忽视的重要性，所以在研究函数的相关问题时如值域、最值、单调性、奇偶性、周期性等，要时刻树立定义域优先的原则。

函数定义域优先原则；最值；参数范围；不等式

函数的三要素是定义域、对应关系和值域。其中函数的定义域是函数的根本，因为函数的定义域如果不同，即使对应关系相同也是不同的函数。这也是区分不同函数的首选条件。函数的其他性质如值域、最值、单调性、奇偶性、周期性等等无不受到定义域的制约。下面就一些常见易错题目进行说明。

一、定义域对值域、最值的影响

例1 已知函数f（x）=2+log3x（1≤x≤9），求函数y=[f（x）]2+f（x2）的值域.

解：因为f（x）的定义域为[1，9].所以要使函数y=[f（x）]2+f（x2）有意义，

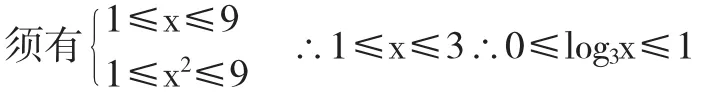
∴当x=3时，即log3x=1时，y的最大值为3.

当x=1时，即log3x=0时，y的最小值为6.

所以函数y=[f（x）]2+f（x2）的值域为[6，13].

本题学生在做题过程中忽略所求函数的定义域，认为所求函数的定义域与原函数的定义域相同得到错解。

二、定义域对单调性的影响

例2 函数y＝log（2-x2+3x-2）的单调增区间是_______；

解析：由-x2+3x-2＞0，得1＜x＜2，

所以函数y＝log（2x2-3x+2）的定义域为（1，2）．

又y＝log2（tt＞0）是增函数，

t＝-x2+3x-2在（1，）上是增函数，

所以函数y＝log2（-x2+3x-2）的增区间为（1，）．

本题学生在做题过程中忽略函数的定义域，直接求真数即二次函数的单调区间等效成所求函数的单调区间，导致所求单调区间超出了函数的定义域而犯错。

三、定义域对周期性的影响

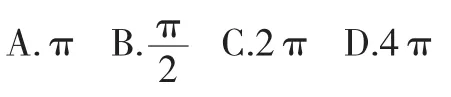
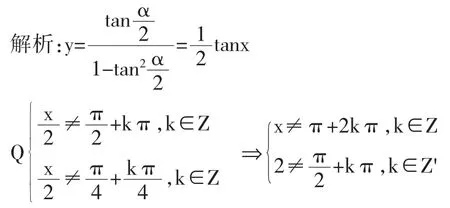
故答案选C.

本题学生在对原函数变形前未考虑函数的定义域，使得函数的定义域前后发生改变，从而得到错误的答案。

四、定义域对奇偶性的影响

所以函数f（x）是奇函数.

点评：这样做忽视定义域的对称性，由定义可知，函数具有奇偶性的必要条件是对于定义域内的任意一个自变量x，必须f（-x）＝f（x）或f（-x）＝-f（x），且-x属于定义域时，才有意义，即定义域必须关于原点对称.

正解：因为f（x）的定义域为{x|x≠-2}，所以函数f（x）是非奇非偶函数.

事实上，如果一个函数的定义域不关于原点对称，那么它一定是非奇非偶函数！因此，我们在判断函数的奇偶性时强调要有定义域“优先意识”.

五、定义域对参数范围问题的影响

例5 设定义在[-2，2]上的偶函数f（x）在区间[0，2]上单调递减，若f（1-m）＜f（m），求实数m的取值范围．

解析：∵f（x）是偶函数∴f（－x）＝f（x）＝f（|x|）

∴不等式f（1－m）＜f（m）⇔f（|1－m|）＜f（|m|）

又当x∈[0，2]时，f（x）是减函数，

本题学生忽略函数的定义域[-2，2]，使得所列条件不足，从而得到错误的答案。

例6 已知函数f（x）=loga（2-ax）在[0，1]上是减函数，则a的取值范围是（ ）.

A.（0，1） B.（0，2） C.（1，2） D.（2，+∞）

解：由题意知a＞0且a≠1，所以t=2-ax为减函数.

又因为f（x）=loga（2-ax）在[0，1]上是减函数，

通过上述几个例子，说明函数的定义域的不可忽视重要性，所以在研究函数的相关问题时如值域、最值、单调性、奇偶性、周期性等，要时刻树立定义域优先的原则，才能避免出现错误。

G633.6

A

1674-9324（2014）07-0246-01