解析几何中的最值距离探析

尹团则

（河北枣强中学，河北 枣强 053100）

解析几何中的最值距离探析

尹团则

（河北枣强中学，河北 枣强 053100）

解析几何中的最值问题是高考中的热点问题，既有选择题，又有填空题、解答题，难度中等偏高.高考题中有关解析几何中求距离最值问题，最终都可以转化为定义或对称思想、三角有界求值域的方法解之，一般思想转折线和为线段最短问题.

数学；解析几何；求线段最值；曲化直

解析几何中的最值问题是高考中的热点问题，既有选择题又有填空题、解答题，难度中等偏高.考查上述问题时，通常考查函数与方程、转化与化归及分类讨论等思想方法.这就要求同学们对最值问题要做到心中有数，运算准确，争取在此类问题上能够脱颖而出.下面，就常常出现的几类题型介绍一下自己的看法.

例1 已知点A（-3，8），B（2，2），点P是x轴上的点，求当|AP|+|PB|最小时点P的坐标.

【解析】设点B关于x轴的对称点为B1，连AB1交x轴于点P，则易知点P满足|AP|+|PB|最小.可求得直线AB1的方程2x+y-2=0.令y=0，则x=1.故所求点P的坐标为（1，0）.

点评：此题考查直线上一点到直线同侧的两点距离和的最小值，往往转化为对称问题，用直线方程的方法求解.很好地把直线问题与几何问题结合到了一起，难度不大，属于易得分题.

例2 若实数x，y满足x2+y2+8x-6y+16=0，则x+y+1的最大值为________.

【解析】解法一：令x+y+1=t，则依题设圆C：（x+4）2+（y-3）2=9与直线l：x+y+1-t=0有公共点，从而故所求最大值为

解法二：因为x，y满足C：（x+4）2+（y-3）2=9，所以可设（θ为参数）.所以x+y+1=3cosθ+3sinθ=3.故所求最大值为

点评：此题考查直线与圆位置关系问题.解法一考虑用圆心到直线距离与半径比较大小，同学们容易想到但要注意计算准确.解法二则巧妙地运用了三角代换方法，简化了运算步骤，是较好的选择.

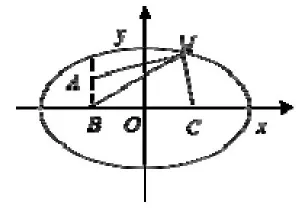
【解析】根据椭圆定义，有|MA|+|MC|=|MA|+（8-|MB|）=8-（|MB|-|MA|）.为使|MA|+|MC|取得最小值，只需|MB|-|MA|取得最大值，A、B、M三点共线时才可以取得，此时，故所求最小值为

点评：此题考查椭圆第一定义的灵活运用，要熟练掌握转化变形，同时应用了三点共线原理，难度稍大，属于拉分题.

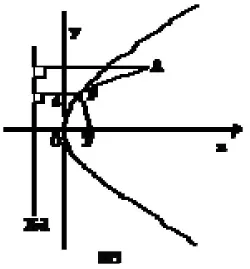
【解析】根据题意，作出右图.显然，O1，O2为双曲线的两个焦点.要使|PM|-|PN|最大，即要使|PM|最大，|PN|最小，以此作出M，N具体位置如右图，则容易得出|PM|-|PN|最大值为：|PM|-|PN|=（|PO1|+2）-（|PO2|-1）=3+|PO1|-|PO2=3+6=9.

点评：此题属于综合性较强的题型，既考查了圆的方程，又考查了双曲线的性质.但最终还是回归到双曲线的定义上，充分体现了回归课本的指导思想.

例5 点A（3，2）为定点，点F是抛物线y2=4x的焦点，点P在抛物线y2=4x上移动，则当|PA|+|PF|取得最小值时，点P的坐标是_____.

【解析】抛物线y2=4x的准线方程为x=-1，设P到准线的距离为d，则|PA|+|PF|=|PA|+d.要使|PA|+|PF|取得最小值，由右图可知过A点的直线与准线垂直时，|PA|+|PF|取得最小值，把y=2代入y2=4x，得P（1，2）.

点评：此题求取最值时，没有上来后先设点，而是首先观察点的位置，看能否借助概念，巧妙进行转化，于是考虑抛物线的定义，顺利解决了此题.

综上所述，高考题中有关解析几何中求距离最值问题，最终都可以转化为定义或对称思想、三角有界求值域的方法解之，一般思想转折线和为线段最短问题.

G633.6

A

1674-9324（2014）07-0241-01