利用基本不等式求最值

郑会英

（河北枣强中学，河北 枣强 053100）

利用基本不等式求最值

郑会英

（河北枣强中学，河北 枣强 053100）

利用不等式求最值是基本不等式的重要应用之一，是高考考查的一个热点，因而灵活运用不等式求最值的方法显得尤为重要，下面就此做一下探索、归纳、总结。

基本不等式；最值；灵活运用

类一：“1”的巧妙运用

变式：已知x＞0，y＞0，x+y-xy=0，推出x+y-xy=0，求2x+y最小值.

类二：巧变形后，利用均值不等式

分析：巧妙变形，变成两项的积或和是定值的类型，再用均值不等式.

类三：基本不等式在实际中的应用

例3 一个水塘的占地面积（矩形）为3200平方米，它的两边都留有宽为4米的参观甬路，顶部和底部都留有宽为8米的休息区，如何选择占地的尺寸，才能使占地面积最少？

分析：认真审题，找出关系式，再用均值不等式解答.

解析：设出矩形的长和宽，表示出占地的面积，利用基本不等式求最值，即可得到结论.

故占地的尺寸为长96m，宽48m.

变式：如图所示，将一矩形厂房ABCD扩建成一个更大的矩形厂房AMPN，要求B在AM上，D在AN上，且对角线MN过C点，已知|AB|＝3米，|AD|＝2米，

（1）要使矩形AMPN的面积大于32平方米，则AN的长应在什么范围内？

（2）当AN的长度是多少时，矩形AMPN的面积最小？并求出最小面积.

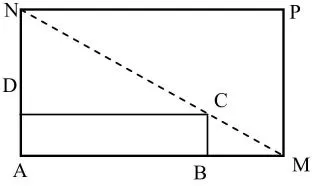
分析：读懂题意，正确找出函数关系式.

根据SAMPN＞32，解关于x的不等式即可.

从函数的角度求最值，可以求导，也可以变换成对号函数的形式利用均值不等式求最值.

即SAMPN取得最小值24（平方米）.

G633.6

A

1674-9324（2014）07-0238-01