课堂教学随笔
——由轨迹求曲线方程想到的
2014-06-27冉邦恒
冉邦恒
(酉阳职业教育中心,重庆 409899)
课堂教学随笔
——由轨迹求曲线方程想到的
冉邦恒
(酉阳职业教育中心,重庆 409899)
在中学数学解析几何中,求动点的轨迹方程,既是学习的重点内容,也是所教的难点之一,特别对于中等职业学校的学生来说更是如此,由于知识结构的差异,多数学生是奔专业乘兴而来最后却扫兴而归.但另一方面,学好这部分知识,对中职学生的专业知识的巩固和专业技能的提升都有极大的帮助.
课堂教学;随笔;曲线方程
如何确定动点轨迹的方程,怎样运用解题方法,在数学学习过程中显得尤为重要.坐标系的选择是基础,不同的坐标系,就有着不同形式的方程,同一坐标系下不会因解法不同而有不同的方程.教学中,首先让学生明白轨迹是具有共同特性的动点的集合,引导学生对于“定点”、“定长”、“定直线”这三“定”的理解(课本上关于圆、椭圆、双曲线、抛物线方程的建立过程,就是求曲线方程的典范,在教学中必须充分发挥其示范作用).拟定与三“定”有关的题目,让学生尝试建立不同的坐标系,如已知△ABC的一边为8,周长为20,求顶点A的轨迹方程.其次,掌握教材中求动点轨迹的最主要最基本的五个步骤,即:(1)建系;(2)设点;(3)列式;(4)代换;(5)化简.无论是自建坐标系,还是已建坐标系,列式与代换是重点,运用不同的知识体系,采取不同的数学手段,由不同的数学表现形式,经过不同的数学处理,最终得出所要的结论,它是数学能力的综合体现.
一、自建坐标系求方程
例:设动点M与两定点A,B所在的直线互相垂直,求动点M的轨迹方程.
解法一:以过AB两定点的直线为X轴,线段AB的中点O为原点,建立直角坐标系,设M(X,Y)为曲线上不与A(-a,0),B(a,0)合的任意一点,由已 知 条 件 MA⊥MB得|MA|2+|MB|2=|AB|2,根据两点间的距离公式,得
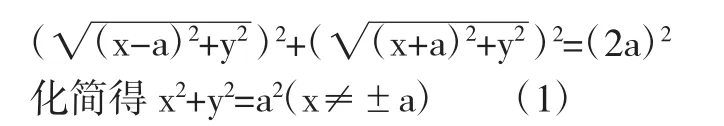

方程(1)即为所求的点M的轨迹方程.
解法二:以通过A和B两定点的直线为X轴,A为原点,建立直角坐标系,如图:

若AB=2a(常量),那么A与B两点的坐标分别为(0,0)和(2a,0)
设M(x,y)为曲线上不与A,B重合的任意一点,可得|MA|2+|MB|2=|AB|2
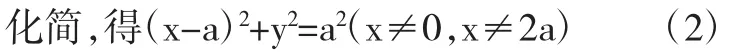
方程(2)也是所求的点M的轨迹方程.
比较方程序(1)(2),可以看出,虽然都是点M的轨迹方程,但由于选择的坐标系不同,所得的轨迹方程的形式也就不同.方程(1)要比方程(2)简单,因此,在建立曲线方程时,要注意选择适当的坐标系,使曲线方程的形式比较简单.
解法三:坐标系的建立同解法一.
设M(x,y)为曲线上不与A(-a,0),b(a,0)重合的任意一点,由已知条件MA⊥MB KAM·KMB=-1
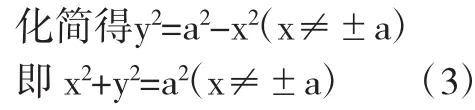
方程(3)也是所求点M的轨迹方程.
比较以上方程可以看出:在同一个直角坐标系中,用不同的方法求出的同一轨迹的曲线方程是相同的.
二、已建坐标系求方程
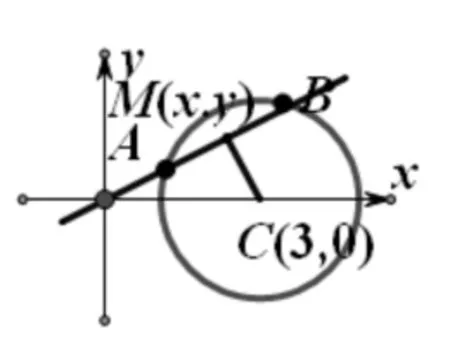
例:过原点的直线与圆x2+y2-6x+5=0相交于A、B两点,求弦AB的中点M的轨迹方程.
解法一:设动点M(x,y),因CM⊥AB,

化简得x2+y2-3x=0(x≠3,x≠0)
解法二:在直角三角形OCM中,OM2+CM2=OC2(x2+y2)+(x-3)2+y2=9
化简得x2+y2-3x=0
所求方程为x2+y2-3x=0
从上两题看出,求轨迹方程问题,要循序渐进,由易到难,充分利用所学知识,寻求不同的解决方法,在不断的探索中寻找乐趣.
G633.6
A
1674-9324(2014)07-0237-01
很少愿意动手去画图,计算的时候更加不愿意动手,而是利用计算器这个数学工具来代替手算。这些小细节对于学习物理都起到了阻碍的作用。第三,学习物理要经常性地在适当的时间做回顾复习。因为物理的知识点相对来说不会特别多,学生可以在学了一个专题之后,对前面的知识做一个简单的回顾,不停学习—复习—学习—复习,这样对知识点的掌握才会更牢固。
