回归课本 注重课本原题在高考题中的应用——余弦定理的又一妙用

宋显梅

（福建省厦门康桥中学，福建 厦门 361000）

回归课本 注重课本原题在高考题中的应用
——余弦定理的又一妙用

宋显梅

（福建省厦门康桥中学，福建 厦门 361000）

余弦定理反映了三角形的一种边角关系，将其转化为单纯的角的关系，对解决一些三角恒等变形问题会起到一种独特的效果。

高考；转化；余弦定理；应用

一、问题的提出

2012年福建省理科高考第17题是本份试卷的一个亮点。一方面它以研究性学习为背景，考查学生运算求解能力、抽象概括能力、推理论证能力，考查特殊与一般思想、化归与转化思想，充分体现了高中新课程的理念；另一方面本题位于试卷的第17题，充分体现出命题组不为难学生和送分的意图，但许多平时水平较高的考生表现并不理想，体现在运算量和时间成本投入较大。2012年福建省状元（有四位学生并列）的数学分数也只在136～139分之间，没有突破140分，这和前面用时较多不无关系，也就说明了这个问题。最后从落脚到探究课本的定理和例题这一视角看，给出的评分标准和标准答案也不是最佳。

【2012年福建省理科高考第17题】回放：

某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数：

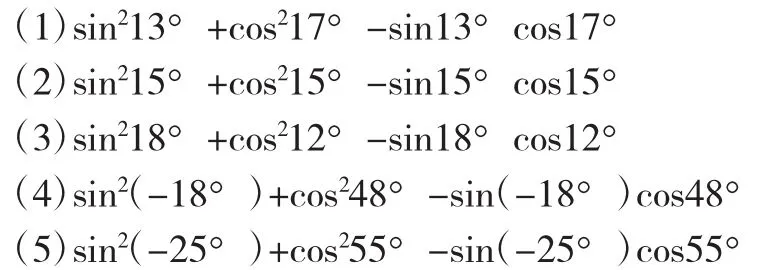
（Ⅰ）试从上述五个式子中选择一个，求出这个常数；

（Ⅱ）根据（Ⅰ）的计算结果，将该同学的发现推广为三角恒等式，并证明你的结论。

（本题的解答见后，需要说明的是该解答属笔者原创。）

二、问题的解决

我们来看下一组题目。求下列三角函数的值：

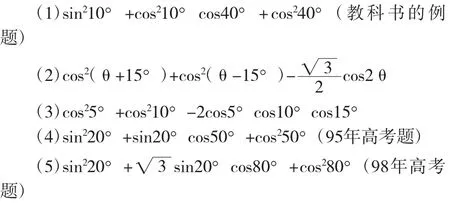
其实它们原于教科书的例题：sin210°+sin10°cos40° +cos240°课本的解法如下：

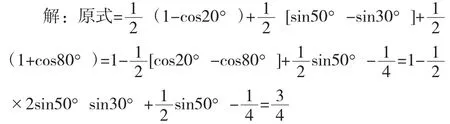
【点评】此解法的利弊很明显，利：比较全面地复习了三角中比较常用的倍半公式、降次公式等公式；弊：运算量较大和加大了时间成本，这将导致运算出现误差和影响后面区分度较大的考题的解答。在当今120分钟要完成22道题（每题约5分钟）的高考中如何缩短时间提高效率显得重要。怎么办？

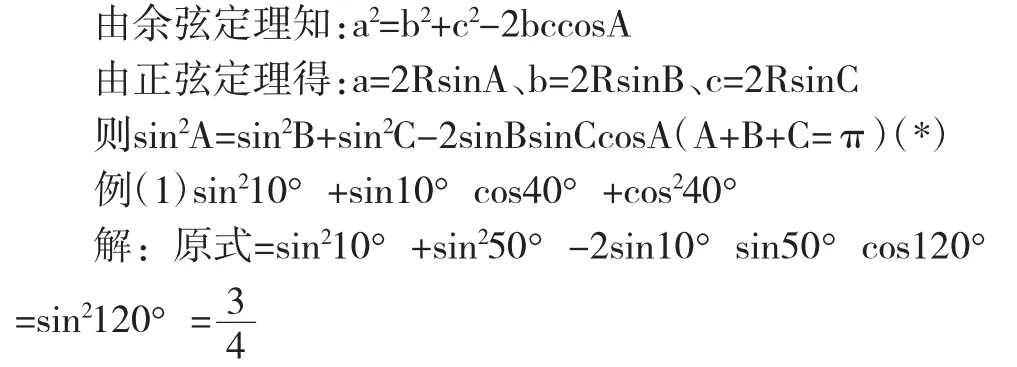
【点评】整个解答运算量小、准确率高、时间成本有效控制，一气呵成、干净利落。

【点评】对类似该组题型的选择和填空题我们利用（*）式可直接得出结果。对该形式的解答题可利用它检查结论：或对（*）式加以证明后（易证）再加以应用。效果比较明显。

三、运用上述推广（＊）对2012年福建省理科高考第17题的原创解答

（Ⅰ）选择（1）式，计算如下：

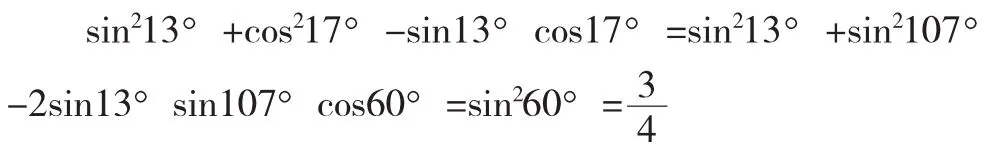
（Ⅱ）三角恒等式为sin2α+cos2（30°-α）-sinαcos（30°-α）=

【高考评分标准如下】：

（Ⅱ）三角恒等式为sin2α+cos2（30°-α）-sinαcos（30°-α）=

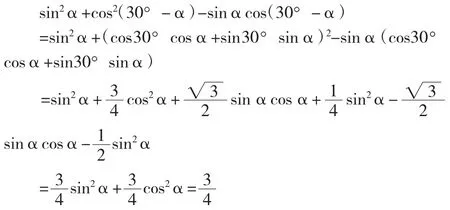
解法二：（Ⅰ）同解法一

（Ⅱ）证明如下：

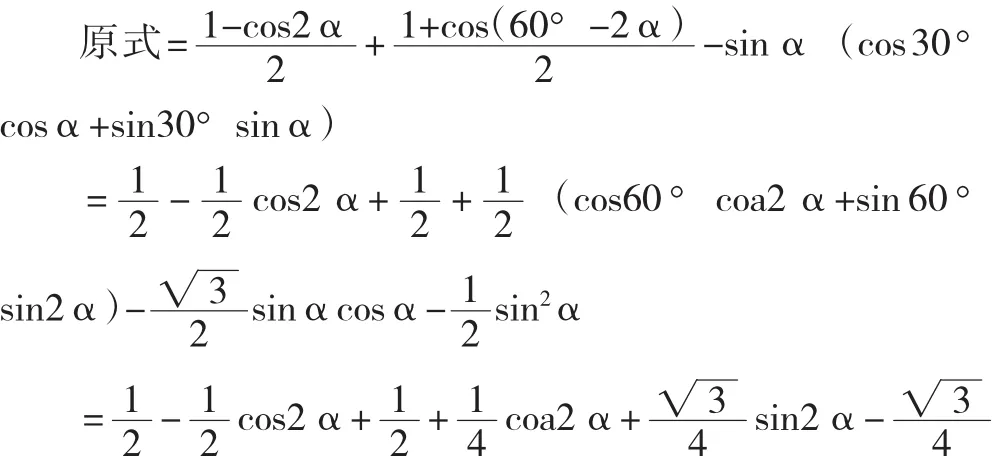
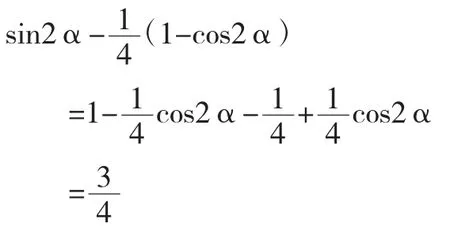
【对比说明】限于文章的篇幅对高考标准答案不再进一步评价。本题原创解法的可取之处在于敏锐地捕捉出它原于教科书的例题，固本朔源，探究余弦定理的等价变形，本题完美解出一举成功拿下，所用时间可以接受。事半功倍。只要我们真正意义上地培养学生创新精神，我们的高三数学迎考将更加有效。

四、结论的推广与证明

下面给出已知：A+B+C=π时sin2A=sin2B+sin2C-2sinB-sinCcosA（*）的推广：

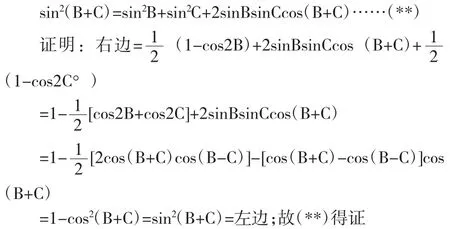
【结束语】

随着高考制度的改革，高考中三角的试题大多来源于课本中的习题和例题或它们的变形，因此复习时应“立足于课本，着眼于提高”，注重等价转化在教学中的应用，在教学中，我们应努力使学生熟练掌握公式的正用、反用、变形用或在特定条件下使用，即注重等价转化在教学中的应用，因为它可以提高思维起点，缩短思维线路，从而使运算流畅自然，缩短时间提高效率。

G633.6

A

1674-9324（2014）07-0231-02