有关卢卡斯数列的充要条件和性质研究

卫 红, 蔺小林

(1.陕西科技大学 信息与网络管理中心， 陕西 西安 710021; 2.陕西科技大学 理学院， 陕西 西安 710021)

0 引言

在经济控制论[1,2]、生态数学、金融理论[3]和组合数学[4]研究中, 经常会遇到斐波那契(Fibonacci)数列和卢卡斯(Lucas)数列以及相关内容等.对斐波那契数列和卢卡斯数列的通项公式的研究一直没有停止过，许多学者[5]应用多种方法来探求他们通项公式的表示方式，应用数学归纳法和前面几项之间的关系来推导他们的一些性质[6-11].本文通过用一个一元二次方程两个根的n次方的和来表示卢卡斯数列的通项公式，给出了卢卡斯数列的一些性质，同时，探讨了斐波那契数列和卢卡斯数列性质之间的一些相互联系.

为了表述方便起见，我们给出斐波那契数列和卢卡斯数列的定义.

定义1设F0=1，F1=1，则满足关系式Fn+2=Fn+1+Fn(n=0,1,2,…)的数列{Fn}称为斐波那契数列.

定义2设L0=2，L1=1，则满足关系式Ln+2=Ln+1+Ln(n=0,1,2,…)的数列{Ln}称为卢卡斯数列.

1 主要结论

对卢卡斯数列进行分析，联系到一元二次方程x2-x-1=0的两个根，我们得到如下有关卢卡斯数列通项公式的一个充分必要条件.

定理设α，β是一元二次方程x2-x-1=0的两个根，则数列{Ln}的通项是Ln=αn+βn(n=0,1,2,…)的充分必要条件是数列{Ln}中任意三项满足关系式Ln+2=Ln+1+Ln(n=0,1,2,…)，并且L0=2,L1=1.

证明：必要性 因为α，β是一元二次方程x2-x-1的两个根，由韦达定理可知：α+β=1，αβ=-1，所以αn+2+βn+2=(α+β)(αn+1+βn+1)-(αβ)(αn+βn)=(αn+1+βn+1)+(αn+βn)

故有

Ln+2=Ln+1+Ln，

在Ln=αn+βn中，令n=0,n=1可得L0=2，L1=1，必要性证毕.

充分性 若L0=2，L1=1，且数列{Ln}中任意三项满足Ln+2=Ln+1+Ln，即

Ln+2-Ln+1-Ln=0

(1)

猜想满足等式(1)的数列通项应该具有如下形式

(2)

其中c1，c2，r1,r2是待定非零常数，把(2)带入(1)，得到

(3)

由于c1，c2，r1,r2是非零常数，所以要(3)式成立，只要下式(4)成立即可，即

R2-R-1=0

(4)

R可以是r1或r2，记(4)式的两个实根分别是α和β，则

Ln=c1·αn+c2·βn

(5)

再根据L0=2，L1=1来确定(5)中的常数c1和c2，得

(6)

注意到α+β=1和αβ=-1，从(6)式中容易求得c1=c2=1，因此

Ln=αn+βn(n=0,1,2,…)

充分性证毕.

2 卢卡斯数列的一些性质

根据上面定理的充分必要条件，容易得到卢卡斯数列的一些性质.

性质1(卢卡斯数列的黄金分割数).

而

所以

即

因此

性质2(卢卡斯数列前n+1项和公式).

证明：

性质3(卢卡斯数列偶数项和公式).

证明：

L2n+1+1.

性质4(卢卡斯数列奇数项和公式)

证明：

α2(n+1)+β2(n+1)-2=

L2n+2-2.

性质5(卢卡斯数列n+1项交错和公式)

证明：

(-1)n+1Ln-1+3.

性质6(卢卡斯数列偶数项交错和公式)

证明：

(-1)nF2n+1.

性质7(卢卡斯数列奇数项交错和公式)

证明：

性质8(卢卡斯数列前n+1项平方和公式)

证明：因为

而

1+(-1)n.

因此

性质9(卢卡斯数列前n+1项立方和公式)

证明：

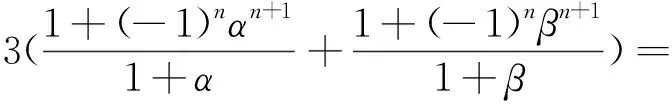
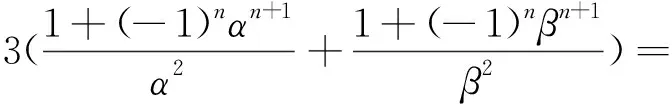
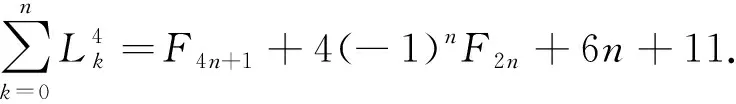
证明：

F4n+1+4(-1)nF2n+6n+11.

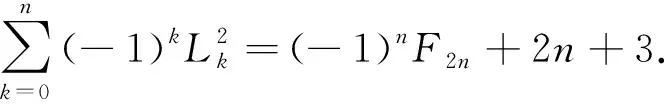
证明：

(-1)nF2n+2n+3.

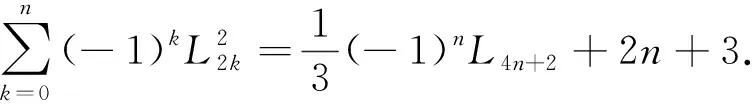
证明：

证明：

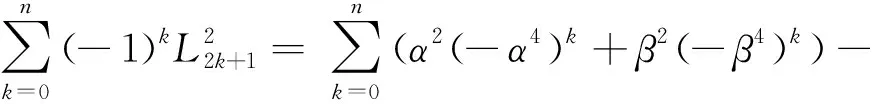
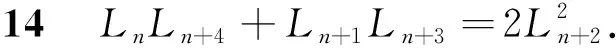
证明：

LnLn+4+Ln+1Ln+3=(αn+βn)(αn+4+βn+4)+

(αn+1+βn+1)(αn+3+βn+3)=

2α2n+4+2β2n+4+(-1)n(β4+α4-β2-α2)=

2α2n+4+2β2n+4+(-1)n(β3+α3)=

2α2n+4+2β2n+4+(-1)n(β2+1+α2)=

2α2n+4+2β2n+4+(-1)n(β+α+3)=

2α2n+4+2β2n+4+4(-1)n=

2α2n+4+2β2n+4+4αn+2βn+2=

性质15LnLn+4-Ln+1Ln+3=10(-1)n.

证明：

LnLn+4-Ln+1Ln+3=(αn+βn)(αn+4+βn+4)-

(αn+1+βn+1)(αn+3+βn+3)=

αnβn+4+βnαn+4-αn+1βn+3-βn+1αn+3=

(-1)n(β4+α4+β2+α2)=

(-1)n(3β2+β+3α2+α)=

(-1)n(4β+3+4α+3)=10(-1)n

3 斐波那契数列与卢卡斯数列性质之间的联系

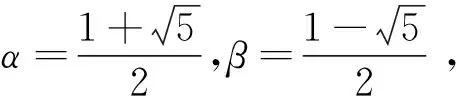
Ln=αn+βn(n=0,1,2,…),

斐波那契数列与卢卡斯数列性质之间有如下的相互联系.

性质16Ln=4Fn-Fn+2.

证明：因为α，β是方程x2-x-1=0的两个根，因此α+β=1，同时有α2=α+1，则4α-α3=α-β，4β-β3=β-α，故

αn+βn.

性质17Ln+Ln+2=5Fn.

证明：

Ln+Ln+2=αn+βn+αn+2+βn+2=

αn(1+α2)+βn(1+β2)=

性质18LnLn+k+1-Ln+1Ln+k=5Fk-1(-1)n.

证明：

LnLn+k+1-Ln+1Ln+k=(αn+βn)(αn+k+1+βn+k+1)-

(αn+1+βn+1)(αn+k+βn+k)=

(-1)nβk+1+(-1)nαk+1-(-1)nαβk-

(-1)nβαk=(-1)nβk(β-α)+

5(-1)nFk-1.

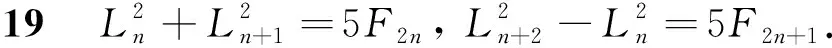
证明：因为

α2n+β2n+2(-1)n+α2n+2+

β2n+2+2(-1)n+1=

α2n(1+α2)+β2n(1+β2)=

而

α2n+4+β2n+4+2(-1)n+2-

α2n-β2n-2(-1)n=

α2n(α4-1)+β2n(β4-1)=

性质20FnLn+1+Fn+1Ln+2=L2n+3.

证明：

α2n+3+β2n+3=L2n+3.

4结论

卢卡斯数列相连三项之间所满足的关系，实际上就是一个二阶差分方程，根据差分方程的求解，容易得到卢卡斯数列的充分必要条件.在卢卡斯数列通项公式基础上，得到了卢卡斯数列的一些经典性质.这些经典性质的一部分在其他一些文献中出现过，只不过那些文献所用证明方法大部分用数学归纳法证明.本文仅用卢卡斯数列通项公式就很容易证明这些，当然，还可以推证出卢卡斯数列其他更多的一些性质，由于篇幅有限，在此不再一一列出，有兴趣的读者可以进行尝试.

[1] 龚德恩.经济控制论[M].北京：高等教育出版社，2010.

[2] 蔺小林，陈壮民.灰色关联度在股票综合评价中的应用[J].陕西科技大学(自然科学版)，2013，31(6)：158-162.

[3] 林支桂.数学生态学导引[M].北京：科学出版社，2013.

[4] 卢开澄,卢华明.组合数学[M].北京：清华大学出版社,2003.

[5] 谭嘉茜.有关斐波那契数列的充要条件[J].数学学习与研究，2013,31(21)：133.

[6] 徐 波.菲波纳斯(Fibonacci) 数列与黄金数[J].黔西南民族师范高等专科学校学报，2002，16(2)：74-76.

[7] 管训贵.Fibonacci数列与Lucas 数列的方幂和[J].贵州大学学报(自然科学版)，2014，31(1)：16-21，26.

[8] Ma Rong,Zhang Rong,Zhang Wenpeng.Severl identities involving the Fibnacci numbers and Lucas numbers[J].The Fibnacci Quarterly,2007,45:164-170.

[9] 赵丹寒，邱永波.Fibonacci数与Lucas数的内在联系[J].中学数学，1996，18(3):31-32.

[10] Zou Xiaowei.A few properties of the Lucas number sequence[J].Journal of Huanggang Normal University,2006,26(3):14-15.

[11] 杨宪立,陈波峰.斐波那契数列与卢卡斯数列的联系及性质[J].河南教育学院学报(自然科学版),1998,7(4):15-18.