超椭圆曲线数字签名算法的改进与实现
2014-06-27刘海峰马畑名刘焕平
刘海峰, 马畑名, 刘焕平
(1.陕西科技大学 理学院, 陕西 西安 710021; 2.陕西科技大学 电气与信息工程学院, 陕西 西安 710021; 3.哈尔滨师范大学 数学科学学院, 黑龙江 哈尔滨 150025)
0 引言
超椭圆曲线加密HCC(Hyperelliptic Curve Cryptography)作为椭圆曲线加密ECC(Elliptic Curve Cryptography)的一种推广,是由Neal Koblitz[1]在1989年提出,其安全性是基于有限域上的超椭圆曲线的Jacobian群上的离散对数问题.(在同等安全水平下,HCC比ECC所用的基域小而且密钥长度更短;一般低亏格(g≤4)的超椭圆曲线的Jacobian离散对数没有发现亚指数时间攻击;并且在同样的定义域上,亏格越大(g≥4)HCC可以提供越多的曲线,这样可供选择用于密码学中的安全曲线空间便增大了;在公钥密码体制中,要获取具有较大阶的有理点群,必须选取相应大的基域,而超椭圆曲线可以在一个很小的基域上构造具有较大素数因子的阶的Jacobian群)[1-3],这些优点使得HCC在密码学界受到越来越多的重视.
以下对已有的超椭圆曲线数字签名算法进行改进,引入平移变换、除子矩阵.并进行了编程验证和结果分析.
1 超椭圆曲线数学理论
1.1 环、域、有限域
定义1.1.1[4]设A是一个非空集合,在A中定义两种二元运算,一种叫加法,记作+,另一种叫乘法,记作*,且满足
(1)
(2)
(3)左、右分配率成立:对任何a,b,c∈A有
a*(b+c)=a*b+a*c
(a+b)*c=a*c+b*c
则称代数系
定义1.1.2[4]设(A,+,*)是环.若A满足:
(1)A中至少有两个元0和1;
(2)A*=A{0}构成乘法群.
则称A是一个除环.若A是一个可换的除环,则称A是域.
定义1.1.3[4]若域
1.2 超椭圆曲线
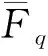
C:y2+h(x)y=f(x)
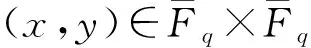
在曲线C上有唯一的一个无限远点∞,特别当g=1时,曲线C即为椭圆曲线.
1.3 除子及除子式
定义1.3.1[8]一个除子D是曲线C上的若干点的一种形式和.
这里只有有限个mp不为0.除子的次数定义为系数的和,即
D在P点的阶为mp,记为ordp(D)=mp.
设Dn表示C上所有除子的集合,那么Dn在如下加法规则之下是一个加法群.
所有次数为0的除子形成的集合D0是Dn的一个子群.

其中ordpR是R(x,y)在P点零化的阶.
定义1.3.3[8]有理函数R(x,y)=G(x,y)/H(x,y)的除子D定义如下:
div(G(x,y))-div(H(x,y))
其中deg(D)=0的除子称为主除子,即D∈D0是主除子.所有除子构成的集合记为P(C,Fqn),因为主除子的次数为0,所以它是D0(C,Fqn)的一个子集.
1.4 Jacobian群[9,10]
商群J(C,Fqn)=D0(C,Fqn)/P(C,Fqn)就是超椭圆曲线C在Fqn上的Jacobian群,记为J(C,Fqn).由定义可知,它实际上就是由一个无限除子群模它的主除子群而得到的一个商群.群中的每一个元素都是一个除子等价类,且表示法不唯一,但在Jacobian商群中的元素都是唯一的.
2 超椭圆曲线数字签名算法协议
超椭圆曲线加密在签名过程中需要将除子唯一的映射到整数域上,此处定义一种映射除子的方法.映射λ表示如下:
λ:J(C,Fqn)→Fq
[a(u),b(u)]→a(u)|u=1+b(u)|u=1∈Fq
公共参数:有限域Fq;超椭圆曲线,其亏格为g,一般选取g≤4,这里令g=2;Jacobian群的基数为lh,l是长度至少为160 bit的大素数(或更大)[11,12],h=1是较小的余因子;基点D=[a(x),b(x)]是阶为l的归约除子,其具有λ映射关系;h( )为160 bit的sha-1函数.以下是对HCDSA算法[8]的描述.
2.1 签名产生阶段
签名产生阶段:Alice对消息m进行签名,其签名过程如下:
(1)随机选择一个大素数dA∈[1,l-1]作为其私钥;
(2)计算QA=dAD作为其公钥,若QA=1则返回(1)重新选择dA;
(3)再随机选择一个大素数kA∈[1,l-1];
(4)计算kAD和r=λ(kAD)modl,如果r=0,则返回到(3)重新选择kA;
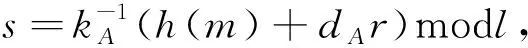
(6)得到签名(m,r,s),Alice将签名传给Bob.
(7)公布公共参数Fq、C、J(C,Fqn)、D、QA、λ.
2.2 签名验证阶段
签名验证阶段:Bob需要先检查这个签名是否Alice发送的,并检查签名的完整性以及是否被篡改,然后进行签名的正确性验证,执行如下步骤:
(1)先获得真实的公共参数及Alice的公钥QA.
(2)计算R=(s-1h(m))D+(s-1r)QA.
(3)检验λ(R)modl=r是否成立,如果成立,则接受签名,否则拒绝签名.
此处不讨论改善除子标量乘算法,重点考虑对原签名算法改进来增强安全性.
3 算法改进方案
下面改进算法中仅阐明需改进的步骤,与HCDSA原算法中相同步骤省略.
3.1 HCDSA上的平移变换
由Jacobian群上的运算封闭性可知,除子的加法运算结果仍然是除子.因此在生成公钥时,引入一个除子DA作为平移量,即将原来的大素数乘除子计算添加一个平移量除子DA,获得新的公钥.由于添加了一个除子,增加了由公钥和公共参数中的除子求解私钥的难度.
3.1.1 签名产生阶段算法改进
将HCDSA算法中的(2)改为
(2)选择一个Jacobian群上的除子DA∈J(C,Fqn);计算QA=dAD+DA作为其公钥;
将HCDSA算法中的(4)改为
(4)计算kAD+DA和r=λ(kAD+DA)modl,如果r=0,则去到(3)重新选择kA;
其他步骤与HCDSA原算法相同.
3.1.2 签名验证阶段算法相应改进
(1)先获得真实的公共参数及Alice的公钥,以及Alice使用的除子;
(2)计算;R=(s-1h(m))D+(s-1r)QA+(1-s-1r)DA;
(3)检验λ(R)modl=r是否成立,如果成立,则接受签名,否则拒绝签名.
这个改进方案中增加了一个除子,每一次签名过程的公钥都是不能通过除子和私钥获得的.而且通过公钥、除子和平移除子获得私钥的难度也被加大.
3.2 HCDSA上比例系数扩展至矩阵上
原签名算法中,由数乘除子获得公钥,安全性是建立在数乘除子的逆运算难解性之上.此处为增加求逆运算的难解性,从而提高安全性,将原来的单一除子扩展为除子矩阵,使得破解运算量急剧增加,从而延长破译时间,增加破译难度[13].除子矩阵的维数将决定破解所需要的时间,n维除子矩阵逆运算所需时间将是原算法的n2倍.
由于使用了矩阵,需要重新定义除子到大整数的映射关系λ,将这个关系定义为除子矩阵集M(J(C,Fqn))到Fq的映射关系,映射要求是单射.那么定义映射关系λ如下:
λ:M(J(C,Fqn))→Fq
对于矩阵中的每个元素有
Mij:[a(u),b(u)]→mij=a(u)|u=1+b(u)|u=1∈Fq
则有映射关系
λ:M(J(C,Fqn))→∑mij∈Fq
在公共参数中的除子D将变为除子矩阵M.其他的公共参数不变.因此获得的公钥也是一个除子矩阵.
3.2.1 签名产生阶段算法改进
将HCDSA算法中的(2)改为
(2)选择一个Jacobian群上的除子矩阵M=M(J,(C,Fqn));计算QA=dAM作为其公钥;
将HCDSA算法中的(4)改为
(4)计算kAM和r=λ(kAM)modl如果r=0,则去到(3)重新选择kA;
将HCDSA算法中的(5)改为
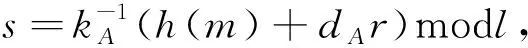
其他步骤与HCDSA原算法相同.
3.2.2 签名验证阶段算法相应改进
将原算法签名验证阶段中的(2)改为计算R=(s-1h(m))M+(s-1r)QA;
检验λ(R)modl=r是否成立,如果成立,则接受签名,否则拒绝签名.
这样的改进将大幅度增加破解签名的计算时间,从而使签名系统更加可靠,在现有的计算机计算能力水平上更加安全.这种改进方法是通过增加公钥到私钥的难解性实现的.
3.3 HCDSA矩阵域上平移变换
为了进一步增加破解计算的时间复杂度,可以对3.2中的矩阵变换增加一个矩阵平移变换.
3.3.1 签名产生阶段算法改进
(1)随机选择一个大素数dA∈[1,l-1]作为其私钥,选择一个除子矩阵域上的矩阵MA∈M(J(C,Fq));
(2)计算QA=dAM+MA作为其公钥;
(3)再随机选择一个大素数kA∈[1,l-1];
(4)计算kAM+MA和r=λ(kAM+MA)modl如果r=0,则去到(3)重新选择kA;
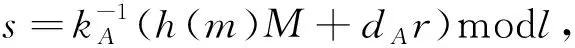
(6)得到签名(r,s),Alice将签名(m,r,s)传送给Bob.
3.3.2 签名验证阶段算法改进
(1)先获得真实的公共参数及Alice的公钥QA,以及Alice使用的除子矩阵MA;
(2)计算;R=(s-1h(m))M+(s-1r)QA+(1-s-1r)MA;
(3)检验λ(R)modl=r是否成立,如果成立,则接受签名,否则拒绝签名.
以上是对HCDSA数字签名协议进行的一些改进.从理论上分析,这些改进都可以增加算法的计算复杂度,从而使得由公钥和已知参数求私钥的难度加大,保证数字签名算法的安全性.
4 改进算法详细实现
超椭圆曲线数字签名相较于目前主流数字签名算法拥有无法比拟的优势 ,目前仍然没有公认的超椭圆曲线数字签名系统的算法实现[8,14,15].此节将在上文中研究的超椭圆曲线数字签名算法以及其改进算法进行实现,并给出实验结果.
4.1 系统参数设置
超椭圆曲线签名体制的实现由它的域参数决定,这些参数主要包括:选择的有限域、超椭圆曲线方程、定义在Jacobian群上的运算、基点和Jacobian群的基数和基点的阶,可以用Fq表示选择的有限域.本文中选择的有限域的特征为2,即选择的域的阶为q=2m(m>80),m为有限域的扩张次数.
(1)C表示超椭圆曲线方程,对于定义在二进制有限域上的超椭圆曲线,它的方程可以简化为y2=x5+kx,所以曲线C可用一个参数k表示;
(2)D为Jacobian群上的基点;
(3)AD为除子的加法运算和除子的倍乘运算;
(4)l为D的阶,即lD=0;
(5)h为协因子,由l·h可以得到Jacobian群Nn.
4.2 算法实例实现
研究表明,亏格为2的超椭圆曲线密码体制只用80bit就可以实现160 bit的椭圆曲线密码体制安全等级.在实例实现中选取83 bit特征为2的超椭圆曲线,T=(Fq,AD,C,D,l,h),具体参数选取如下:
(1)C:y2=x5+3x
(2)q=1208925819614629175095961
(3)l=1461501637332961738997140052922
587693332824903681
(4)h=2
(5)D:([1153039623590221879207244813
4599638491234677823851],[12078432950553317
64911960110423416949478906188636])
输入待处理的明文m:Hyperelliptic Curve Digital Signature Algorithm
经过SHA-1算法后的消息为:
6937e5c1e2f76ae9c0a58e48254e56ca8d3bf5af
三种方式的改进签名算法执行过程中产生的参数,以及签名结果和签名验证结果如表1所示.

表1 平移变换后签名算法

表2 矩阵域上的签名算法

表3 矩阵域上平移变换后签名算法
5 改进算法性能分析
5.1 算法安全性分析
该改进的算法在不增加密钥长度的情况下增强了数字签名的安全性.在改进的算法中,通过增加除子使得公钥的计算更加复杂,因此破解者企图通过公钥和公共参数中的除子破解私钥变得更加困难.
将原算法中除子改进为除子矩阵后,私钥与除子的乘扩展为私钥与除子矩阵的乘,除子矩阵的维数决定了算法的计算量及安全程度.n维除子矩阵的逆运算是普通除子的n2倍.引入除子矩阵后,攻击者通过除子矩阵破解私钥的计算量将大大增加.与原算法单除子相对比,从计算复杂性上保证了该算法的安全性.
平移变换的引入,也使得破解者需要进行更多的变换运算,即更大的计算量来求解私钥,增加了算法的安全性.
5.2 时间性能分析
在时间性能损失不大的前提下增加了超椭圆曲线数字签名算法的安全性.通过实验数据可以看出,改进的算法并未优化时间性能,有一定的时间性能损失,但相对于算法整体计算量耗时可以忽略不计.从用户体验角度看,该算法相对原算法时间差距可以忽略.综合考虑安全性的提升以及时间性能的损失,改进的算法具有一定的应用价值,这对后续研究超椭圆曲线密码体制有一定的启示作用.
6 结束语
本文主要对超椭圆曲线数字签名算法进行了三方面的改进:对获得公钥的过程增加了平移变换;将计算过程中Jacobian群除子变换成Jacobian群上的除子矩阵,增加计算复杂度;通过对除子矩阵增加平移变换进一步提高安全性,并在大素数有限域上提供了算法实现实例.对算法性能的分析表明:改进的算法虽损失了少量时间性能,但安全强度较之原算法有很大的提高,具有广阔的实际应用前景,进一步突出了超椭圆曲线数字签名相比于目前主流数字签名算法拥有的无法比拟的优势.
[1] Koblitz N.Hyperelliptic Cryptography[J].J of Crypto,1989,1(3):139-150.
[2] 陈 雁.基于超椭圆曲线密码体系的数字签名技术[D].武汉:武汉理工大学,2007.
[3] Wang Hui,Zhang Fangguo,Wang Yumin.The software implementation of the elliptic curve cryptosystem over large prime fields[J].Journal of Xidian University,2002,29(3):426-428.
[4] 胡冠章.应用近世代数[M].第2版.北京:清华大学出版社,1999.
[5] Gaudry P,Harley R.Counting points on hyperelliptic curves over finite fields[C]//Lecture Notes in Computer Science.Berlin Heidelberg:Springer,2000:313-332.
[6] 陈玉春,朱艳琴.超椭圆曲线盲数字签名方案的设计[J].信息安全与通信保密,2007,29(7):101-102,105.
[7] 于贺威.超椭圆曲线群快速算法研究[D].成都:西南交通大学,2011.
[8] 叶志勇.超椭圆曲线密码协议的研究与应用[D].苏州:苏州大学,2009.
[9] 陈小娥,游 林,何 佳.基于超椭圆曲线Jacobian群的不可否认数字签名[J].海南师范大学学报(自然科学版),2008,21(2):123-125.
[10] 陈智雄,黄振杰,肖国镇.超椭圆曲线上的Jacobian加法算法的优化[J].西安电子科技大学学报(自然科学版),2005,32(6):922-926.
[11] 付治国,术洪亮,张树功.亏格为3的超椭圆曲线除子类的计算公式[J].吉林大学学报(理学版),2009,47(2):201-206.
[12] 梅 挺,何大可,张仕斌.椭圆与超椭圆曲线密码体制的研究与进展[J].计算机工程与科学,2007,29(6):10-13.
[13] 严 爽.有限域上超椭圆曲线离散对数问题的错误攻击问题[D].济南:山东大学,2013.
[14] 蔡庆华.一个基于超椭圆曲线的代理签名[J].计算机技术与发展,2010,20(7):160-163.
[15] 朱艳蕊.超椭圆曲线标量乘快速算法研究[D].成都:西南交通大学,2010.
