摆线钢球行星传动机构设计与仿真分析

2014-06-27高东强

陕西科技大学学报 2014年6期

高东强，王伟

(陕西科技大学机电工程学院，陕西西安 710021)

0 引言

摆线钢球减速器是一种特殊形式的行星齿轮传动，其利用钢球作为中间介质，在一条内、外摆线槽构成的循环滚道中作啮合运动，从而传递运动和动力.它具有传动比大、传动效率高、体积小等优点，应用前景相当广阔，但该减速器目前仍处于设计研究阶段，其产品还尚未成熟[1].

利用三维建模仿真技术，可以在机械结构设计过程中，进行零件之间的装配和运动仿真，帮助设计人员及时发现和解决存在的问题.Pro/E是世界上目前应用非常广泛的一种三维造型软件，其在三维零件的建模方面具有非常强大的功能，但在零件的运动仿真方面存在不足；ADAMS是行业中目前使用最为广泛的机械系统动态仿真软件，广泛应用于航空航天、汽车工程、铁路车辆、工程机械等领域，但其却在建模方面功能较差.

本文通过联合运用Pro/E和ADAMS等两种软件，对二级摆线钢球减速器的结构进行三维造型设计和运动仿真，可以大大地提高结构设计的效率和准确性，从而为结构设计和性能改善提供思路和依据[2].

1 摆线钢球行星传动的特点

1.1 结构特点和传动原理

摆线钢球行星传动是一种特殊形式的K-H-V型行星传动机构，具有传动比大、啮合效率高、体积小等优点，目前已经成为人们关注的焦点.以二级摆线钢球行星减速机构为研究对象，其结构形式如图1所示.

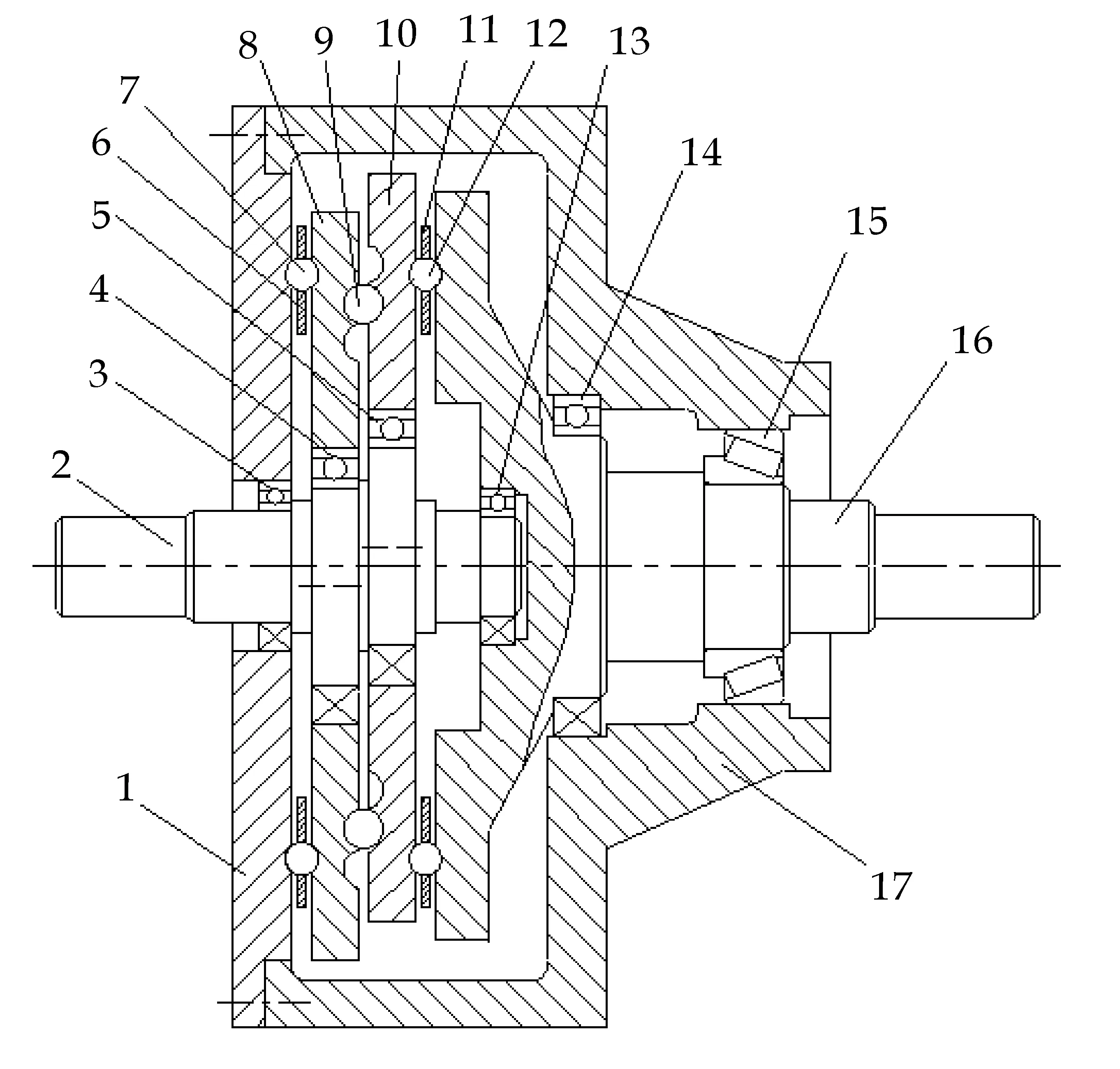
1.中心盘 2.输入轴 3、4、5、13、14.滚动轴承 6、11.保持架 7、9、12.钢球 8、10.偏心盘 15.圆锥滚子轴承 16.输出盘 17.壳体图1 摆线钢球行星传动结构简图

固定盘1和偏心盘8之间通过钢球7啮合传动，构成第一级减速机构；钢球9在偏心盘8和偏心盘10组成的环形槽中运动，构成环形槽等速输出机构；偏心盘10、输出盘16和钢球12之间的啮合运动，构成第二级减速机构.

当输入轴2以角速度ω1等速转动时，其偏心轴段通过滚动轴承带动偏心盘8旋转，中心盘1固定，其与钢球7之间的约束作用反推偏心盘8自转，实现第一级减速；然后，偏心盘8通过环形槽等速输出机构，驱动偏心盘10等速旋转；而偏心盘10则通过钢球12推动输出盘16以更低的角速度ω2输出，实现第二级减速[3].

1.2 短幅内、外摆线理论廓线方程

半径为r的滚圆，在固定不动的半径为R的基圆上，作无滑动的纯滚动时，滚圆圆周上一点的轨迹即为外摆线，而滚圆内一点的轨迹即为短幅外摆线.

在直角坐标系下，短幅内、外摆线的方程式如下：

(1)短幅外摆线的理论廓线方程为：

(1)

(2)短幅内摆线的理论廓线方程为：

(2)

由内、外摆线的方程式可见，摆线的基本设计参数为nb，r0，k1.

1.3 钢球运动位置方程

在直角坐标系下，钢球位置方程为：

(3)

其中，m的取值为1，2，3,…,nb-1.

2 结构设计

以二级摆线钢球减速机构为例，其初始条件定义为：输入转速n1=1 000 r/min，功率P1=0.5 kW，第一级传动比i1=8，第二级传动比i2=8.端齿盘要求高的硬度、强度、耐冲击、耐疲劳和耐磨损，摆线盘材料可选择渗氮钢38CrMoAl和38CrMoAlA[4].

2.1 结构类型的选择

根据内、外摆线盘以及W机构的不同位置，一级摆线传动机构有4种结构类型，分别为Ⅰ型、Ⅱ型、Ⅲ型、Ⅳ型等.二级摆线传动机构是由两个一级传动型式串联或并联而形成的，第一级可以是Ⅰ型或Ⅱ型，第二级可以是Ⅲ型或Ⅳ型[5].

如图2所示，其结构类型是Ⅰ型和Ⅲ型的并联组合，其输入与输出同向.

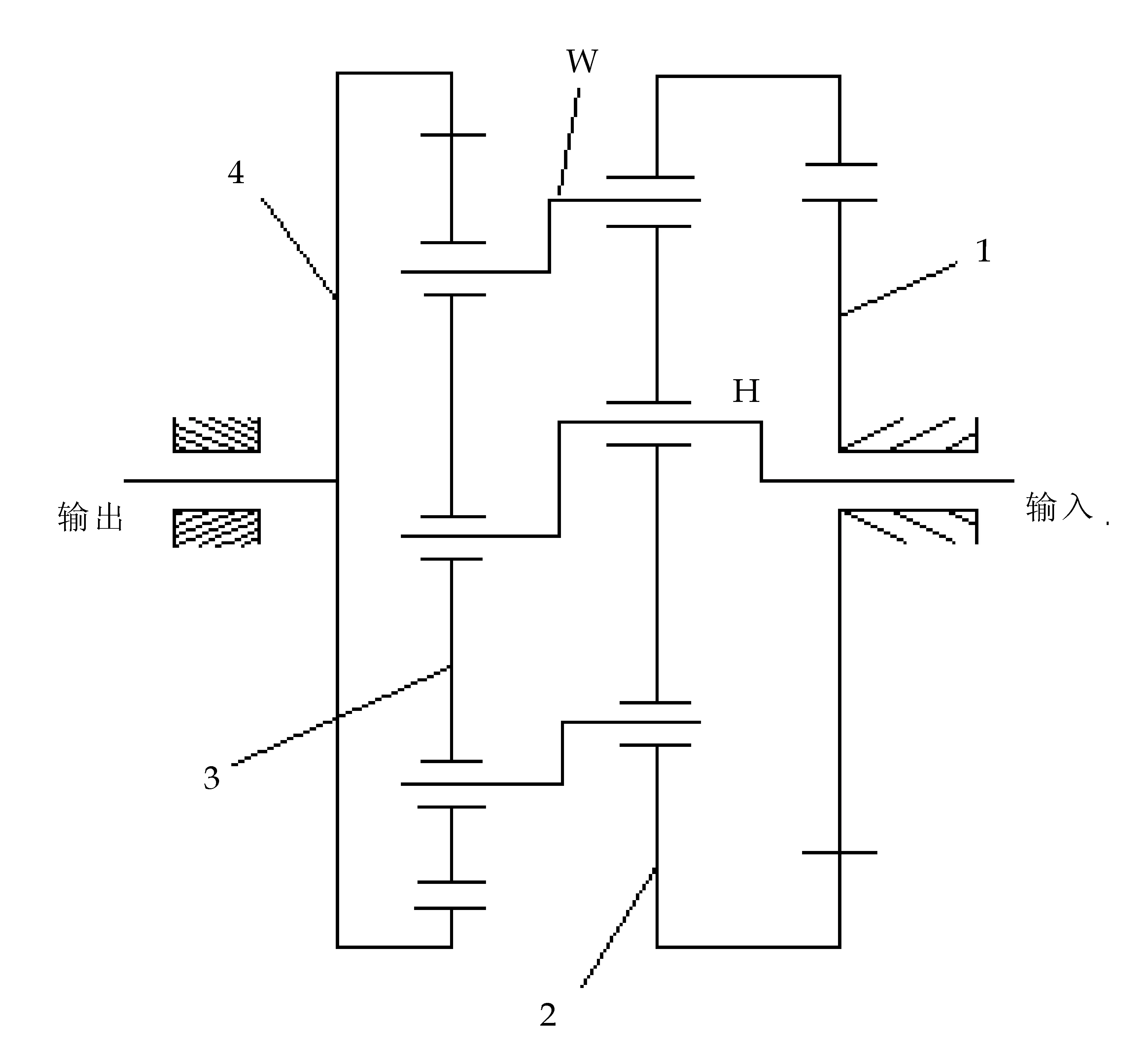
图2 结构类型

输入轴上的两个偏心盘心呈180 °的偏心分布，且偏心距相等，其外形和重量相同，可以依靠自身的结构满足动平衡的要求[5].

2.2 传动比的计算

图2所示的二级摆线钢球行星传动机构是一个周转轮系.其中,1为外摆线中心盘，2为内摆线偏心盘，3为外摆线偏心盘，4为内摆线输出盘，H为行星架，W为环形槽等比输出机构.

给周转轮系加上一个公共角速度ωH，转化为定轴轮系，其各构件相对角速度为[6]：

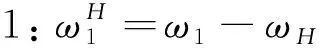
(4)

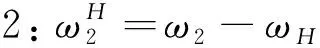
(5)

(6)

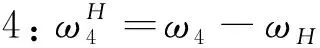
(7)

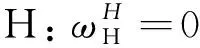
(8)

根据公式(4)～(8)，计算输出盘和中心盘的相对角速度为:

(9)

所以，二级摆线钢球行星传动机构的总传动比计算公式为：

(10)

根据公式(10)可知，只要知道内、外摆线盘的波数，就可计算出二级减速机构的传动比.对于Ⅰ型和Ⅲ型的传动机构，其传动比都为内摆线波数的一半，所以：

钢球数nb1=nb2=15.

摆线盘波数Z1=Z3=14，Z2=Z4=16.

二级摆线钢球传动机构的总传动比为：

2.3 等速传动机构

等速传动机构是摆线钢球行星传动机构的重要组成部分，它将摆线盘的行星运动转化为定轴运动，又称之为W输出机构.

输出机构的种类有多种，如孔销式等速传动机构、浮动盘式等速传动机构、钢球环槽式等速传动机构、钢球直槽式等速传动机构等[7].图3所示为钢球环槽式输出机构，其利用钢球和环形槽之间的无隙啮合，实现两个平行轴间运动和动力的传递，是一种精密等速输出机构.

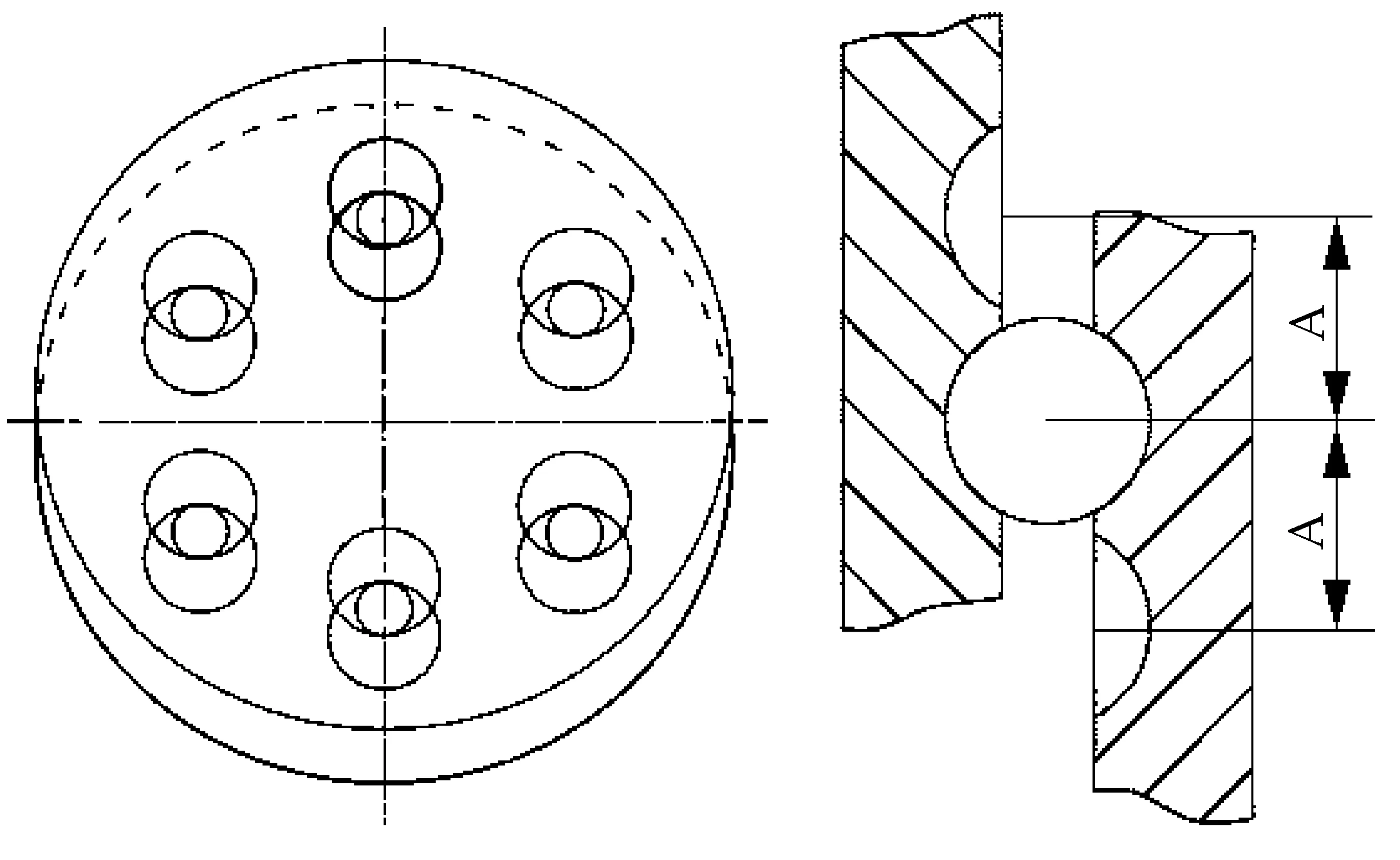
图3 环形槽等比输出机构

对于二级摆线钢球传动机构，输入轴上有两个偏心180 °布置的偏心盘，且偏心距相等(A=2e).如图3所示，偏心盘表面各有6个环形槽，两环形槽的中心距为2倍的偏心距，即钢球的直径dW=2A=4e.

2.4 设计实例

(1)计算输入输出力矩[8]

电机输入力矩计算公式为：

(11)

将初始条件代入公式(11)，可得

输出力矩计算公式为：

T输出=T输入×i×η

(12)

在公式(12)中，取η=90%，则可得:

T输出=4 775×4.267×90%=18 337.4 N·mm

在实际中，因机构存在制造误差、载荷分布不均匀等，其实际输出力矩为：

T实际=T输出×(1+10%)=2 017 N·mm

(2)计算钢球分布圆半径

初步计算分布圆半径的经验公式为[8]：

(13)

在公式(13)中，取经验系数q=2.6，则Rb=35.388 mm，初步选取Rb为40 mm.

(3)计算短幅系数K1和偏心距e

nb为15，K1的取值范围为0.42～0.63[9]，初步选取K1=0.46,又Rb=(nb*e)/K1，所以e=1.227，圆整为1.5，重新计算Rb=48.913 mm，圆整为Rb=50 mm，可得K1=(nb*e)/Rb=0.45.

(4)计算钢球半径rb

短幅内、外摆线是滚圆在基圆上滚动而形成的，而摆线钢球传动的实际啮合齿廓是钢球和理论曲线的等距曲线之间的啮合，故钢球半径rb不应超过滚圆半径r0.

滚圆半径r0=e/K1=3.268，取rb=2.

(5)钢球和摆线槽啮合角β

β角由钢球和摆线槽的截面半径确定，是XY平面和空间法向力的夹角，如图4所示.

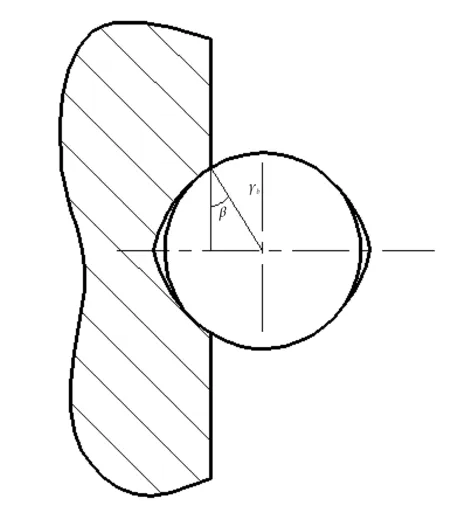
图4 啮合槽

摆线槽深度t1=(0.5～0.8)rb[10]，取t1=0.6,rb=1.5 mm，由图4计算可知β=23.6 °，圆整为30 °，即β=0.523 6.

(6)环形槽钢球分布圆半径Rw

为了避免偏心盘左右端面上摆线槽和环形槽出现交叉，应使环形槽钢球分布圆直径Dw与钢球直径dw的2倍之和小于偏心盘根圆直径Df，即

Dw+2dw≤Df

(14)

其中,Df=2Rb-2e-2rb，由公式(14)得

Rw≤Rb-5e-rb=40

取Rw=36 mm.

(7)环形槽深度t2=(0.6～0.8)rw，取t2=0.7,rw=1.4,e=1.75 mm.

(8)摆线槽根切约束公式为[11]：

(15)

将以上计算结果代入公式(15)可知，G=-0.122，则说明所设计的结构参数满足摆线槽根切约束条件.

3 关键零部件的参数化建模

3.1 内、外摆线的参数化

内、外摆线盘表面上刻有内、外摆线形成的一条循环滚道，钢球与其啮合传动，内、外摆线盘建模的关键在于内、外摆线的参数化.根据方程式(1)和(2)，在Pro/E中输入外摆线的基本参数，通过从方程命令，输入外摆线的参数方程，如下所示：

theta=t*360

x=nb*r0*cos(theta)-k1*r0*cos(nb*(theta))

y=nb*r0*sin(theta)-k1*r0*sin(nb*(theta))

z=0

系统自动生成外摆曲线，同样的方法可参数化生成内摆线，如图5所示[5].

(a)外摆线 (b)内摆线图5 参数化内外摆线

3.2 摆线槽的参数化

摆线槽的截面形状有单圆弧、双圆弧、梯形、三角形、抛物线等多种型式.图4所示截面形状为双圆弧型滚道，其特点为钢球与滚道多点接触，传动平稳，精度高，承载能力强[6].

在参数设置中，输入钢球半径Rb、啮合副槽型半角β，利用Pro/E中的扫描切口命令，绘制摆线槽的截面形状，并定义内、外摆线的理论曲线为扫描轨迹线，从而扫描生成内、外摆线槽，结果如图6所示.

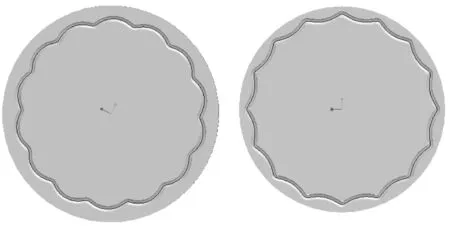
(a)外摆线槽 (b)内摆线槽图6 参数化摆线槽

3.3 环形槽等速传动机构

环形槽等速传动机构是摆线钢球减速器的重要组成部分，它将摆线盘的行星运动转化为定轴运动，两环形槽的中心距等于输入偏心轴的2倍偏心距[7].

在Pro/E参数设置中，输入环形槽钢球分布圆半径RW、环形槽深度t2、偏心距e，扫描切口生成环形槽，如图7所示.

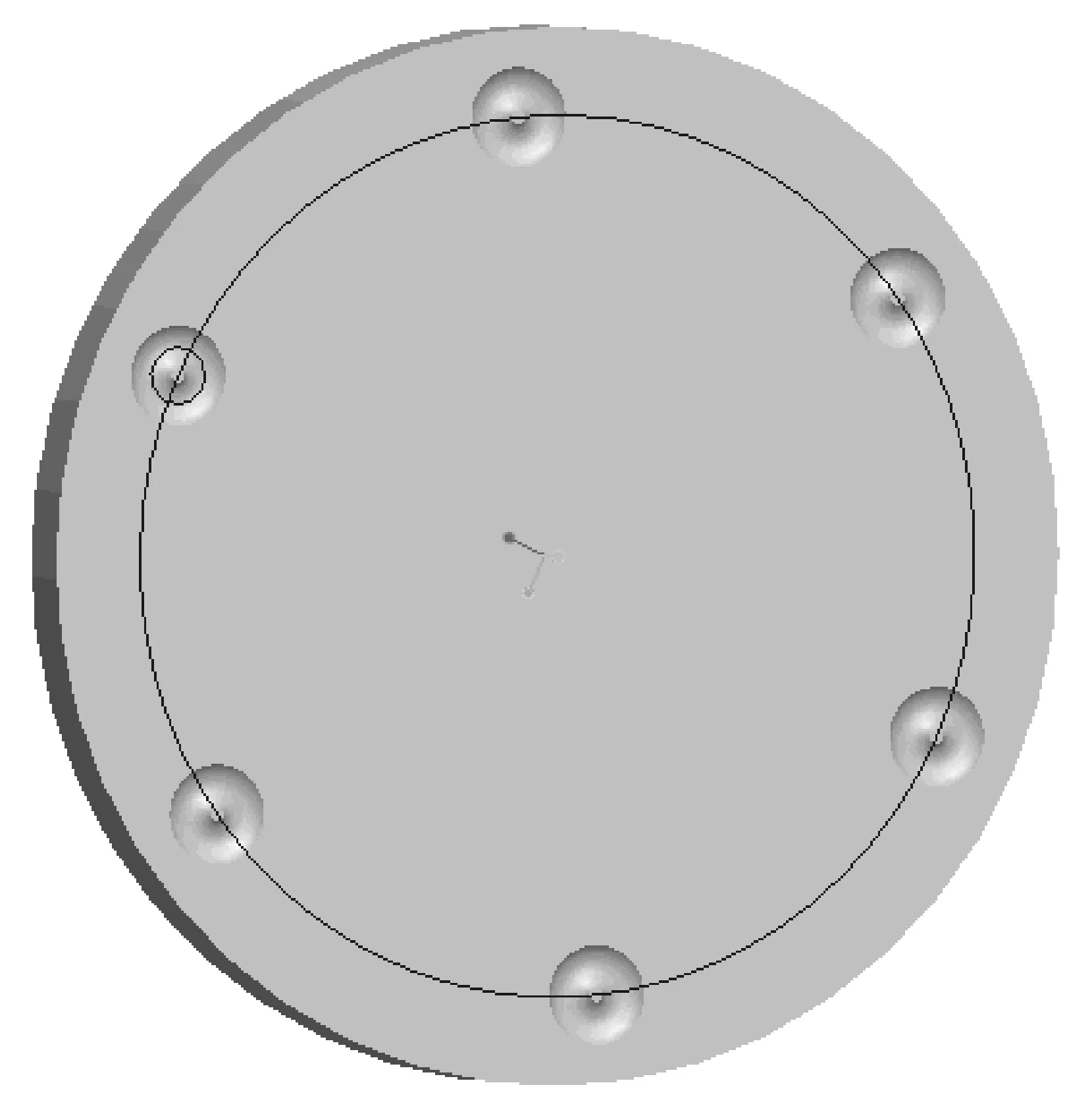
图7 参数化环形槽

3.4 主要零件的三维模型

摆线钢球减速器的关键零件是中心盘、偏心盘、输出盘、偏心输入轴等.利用Pro/E的参数化功能，通过驱动摆线的方程式，以及对尺寸的驱动，可实现摆线钢球减速器的参数化和系列化.以下为二级摆线钢球减速器主要零件的三维造型，如图8所示[12].

(a)中心盘 (b)环形槽 (c)偏心盘

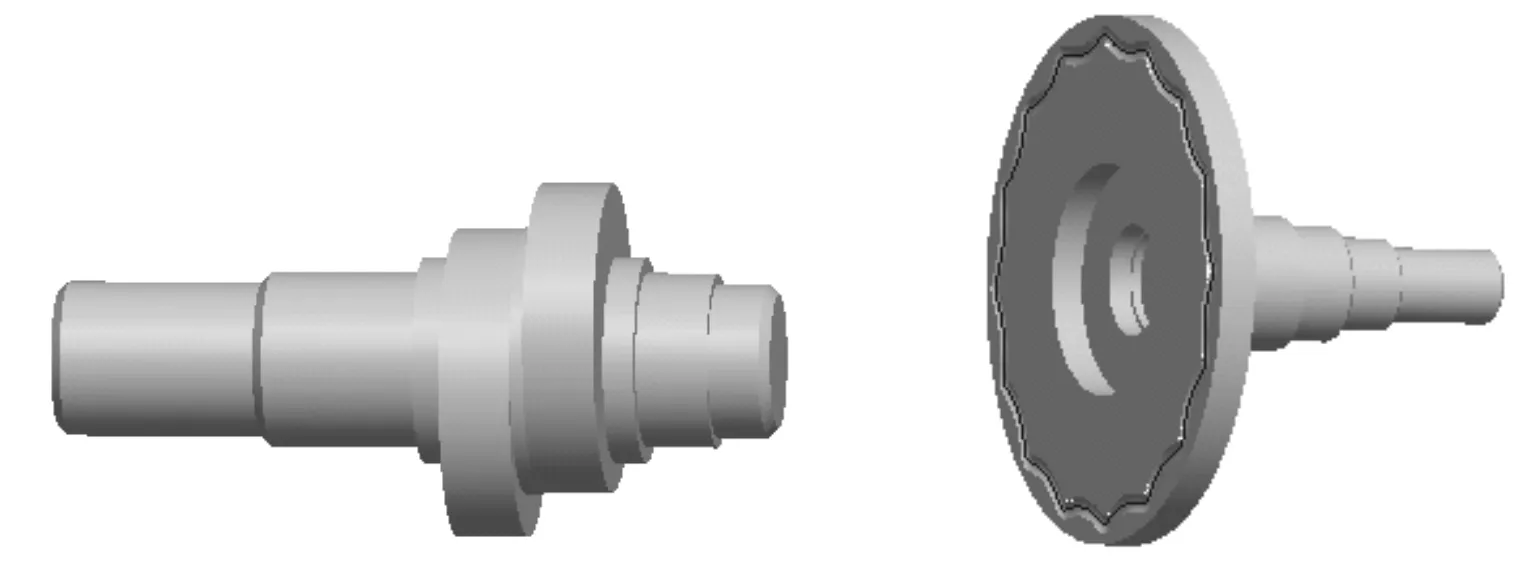
(d)输入轴 (e)输出盘图8 实体模型

4 Pro/E和ADAMS的联合仿真

4.1 Pro/E环境下的装配

摆线钢球行星传动，实质上是钢球和一条内、外摆线形成的循环滚道进行啮合传动，钢球的中心轨迹是一条短幅摆线，实际的工作齿廓是短幅摆线的等距曲线.

啮合传动时，内、外摆线的啮合点(切点)，即为运动过程中钢球的位置.所以装配时，必须将钢球和内、外摆线槽正确地装配到一起，以保证运动仿真时，钢球与内、外摆线槽正确啮合.

利用Pro/E的装配功能，通过零件特征之间几何尺寸的约束，对二级摆线减速器的中心盘、输入轴、钢球、偏心盘、输出轴以及壳体等进行装配，如图9所示.

(a) 装配体

(b)分解图图9 零件的装配与分解

4.2 ADAMS环境下的仿真分析

利用Pro/E的装配功能，可以将钢球和内、外摆线槽正确地装配到一起，但无法正确仿真钢球和内、外摆线槽的啮合运动;ADAMS的建模能力较弱，但在机械零件的运动仿真方面具有较强功能.将图8所示的装配模型导入ADAMS中，仿真二级摆线钢球减速器的运动，并进行分析.

钢球和摆线槽为多点接触，其间的载荷分布复杂，会产生接触变性的影响，在ADAMS中假设零件为刚体，各零件设置约束如下：

(1)中心盘设置为固定副约束.

(2)偏心轴、偏心盘、输出盘等均设置为旋转副约束.

(3)钢球分别和内、外摆线盘之间施加接触力(Solid to Solid).

(4)钢球和保持架之间分别设置接触力(Solid to Solid).

(5)偏心轴和两个偏心盘之间分别设置接触力Solid to Solid).

系统中共有固定副1个、旋转副4个、接触力104个,如图10所示[13].

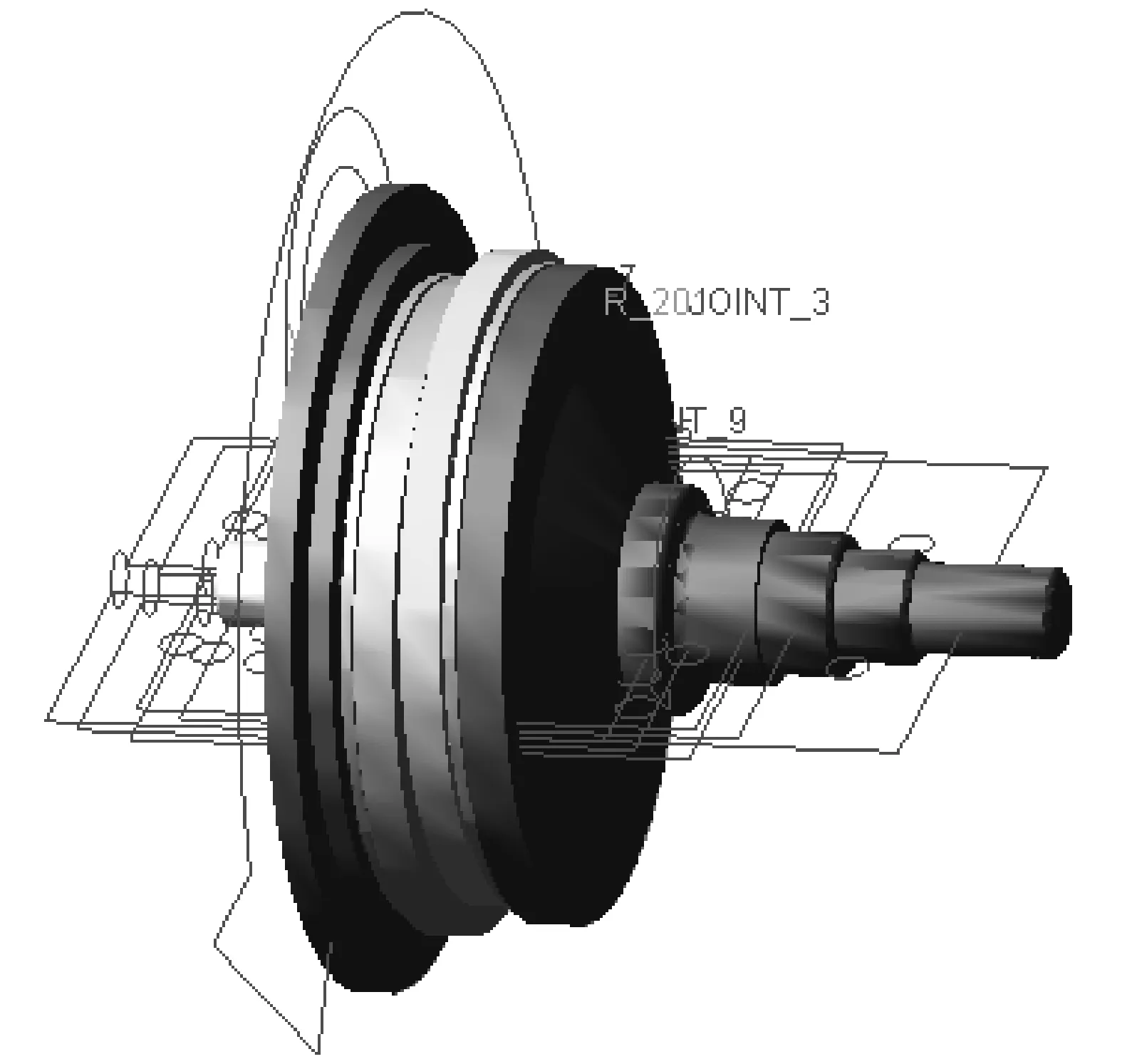
图10 仿真模型

对输入轴添加旋转驱动副，速度设置为60 °/s，其仿真结果如图11所示.

(a)偏心盘8和偏心盘10角速度曲线

(b)偏心盘8和偏心盘10角加速度曲线

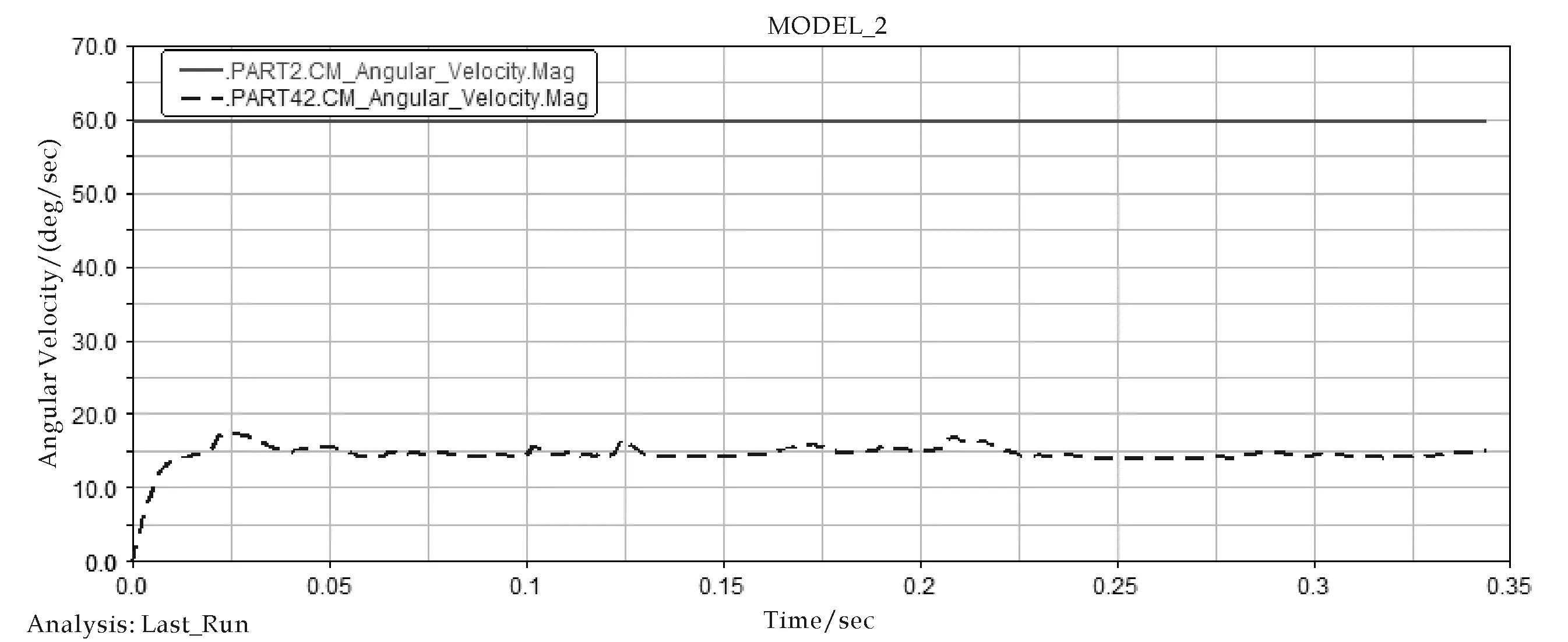
(c)输入轴2和输出盘17角速度曲线图11 仿真曲线

摆线钢球行星传动机构是无隙啮合传动，利用钢球和摆线盘的啮合来传递运动和动力，具有运动平稳、重合度大等特点.钢球9在偏心盘8和偏心盘10组成的环形槽中运动，构成环形槽等速输出机构.

由图10(a)和(b)可知，两个偏心盘的角速度曲线和角加速度曲线近似，角速度趋近于7.5 °/s，角加速度趋近于0，钢球和内、外摆线盘的啮合运动逐渐趋于平稳.由图10(c)角速度曲线可知，输出盘的角速度曲线趋近于15 °/s，输出盘的运动趋于平稳，为等速运动.

根据前述分析计算可知，减速器第一级的传动比i1=8，总的传动比I=4.267.由图10(a)可知，输入轴为60 °/s，第一级偏心盘的角速度为7.5 °/s，减速比为60/7.5=8，与前述理论计算结果一致.由图10(c)可知，输出盘的角速度为15 °/s，总的减速比为60/15=4，与前述理论计算结果一致.

通过ADAMS的仿真分析，说明了结构运动的合理性，这为该减速器样机的结构设计和仿真分析提供了理论依据.