考虑微观孔喉结构的相对渗透率计算方法

田虓丰， 程林松， 李翔龙， 霍啸宇， 毛文辉， 蒋丽维， 侯 涛

(1.中国石油大学(北京) 石油工程学院， 北京 102249； 2.中国石油大学 (北京) 地球科学学院， 北京 102249； 3.中国石油华北油田山西煤层气勘探开发分公司 地质研究所， 山西 晋城 048000)

0 引言

随着常规油气资源的枯竭，超低渗透油藏已成为我国能源增储上产的主要物质基础，是“十二五”规划中长庆油田上产5 000万吨、大庆油田稳产4 000万吨的保障.相对渗透率曲线对油田开发起到至关重要的作用.而微观孔喉结构对相对渗透率曲线又有着显著的影响.

根据孔喉分布计算相对渗透率曲线已经过了60多年的发展[1-8]，但是由于没有考虑边界层和贾敏效应的影响，因此对超低渗透油藏的适用性较差，表现为：(1)无法计算残余油与束缚水饱和度；(2)水相端点为1.

本文针对以上两个问题，通过微圆管实验[9-13]和水锁实验[14]分别得到了边界层厚度的计算公式和渗透率损失程度图版，对Brooks-Corey模型进行修正，得到了一个适用于超低渗透油藏的相对渗透率计算方法.

1 束缚水和残余油饱和度

超低渗透油藏中束缚水和残余油由两部分构成，一是边界层流体，二是不连通孔喉中的流体.因此要确定束缚水和残余油饱和度，需要先计算边界层流体饱和度和不连通孔喉中的流体饱和度，再根据润湿性将其进一步细分为束缚水和残余油饱和度.

1.1 边界层中束缚水和残余油饱和度

1.1.1 边界层流体饱和度

通过对微圆管实验的[9,10]数据重新整理分析发现，单根微圆管中边界层厚度比例与流体粘度呈线性关系，与微圆管半径呈乘幂关系，当压力梯度小于1 MPa/m时与压力梯度呈指数关系，大于1 MPa/m时近似不变.通过对实验结果进行拟合建立了单根微圆管中边界层厚度的计算公式：

(1)

式中，h—边界层厚度，μm；r—微圆管半径，μm，<10μm；p—压力梯度，MPa/m；μ—粘度，mPa·s.

假设岩心是由半径从rmin到rmax连续分布的微圆管组成，当孔喉中为单相流体时的边界层流体饱和度为：

(2)

式中，Sb—边界层流体饱和度；αi—半径为ri的微圆管所占体积比例；hi—半径为ri的微圆管边界层厚度，μm.

由于相渗实验中压力梯度远大于1 MPa/m，因此hi采用大于1 MPa/m时的公式计算.

1.1.2 边界层流体中束缚水和残余油饱和度

由于岩心内部润湿性分布复杂，并非单一润湿，因此使用润湿指数来进一步区分不可动流体中束缚水和残余油.按照表1中润湿性的分类标准，假设润湿指数为I，则不可动流体中束缚水和残余油的比例为：

(3)

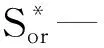
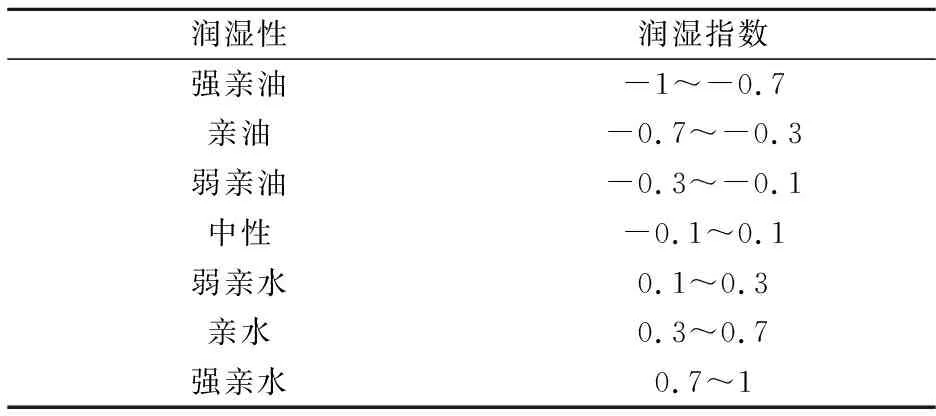
表1 润湿性分类

根据润湿性计算边界层流体中束缚水和残余油的饱和度为：

(4)

(5)

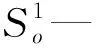
1.2 不连通孔喉中束缚水和残余油饱和度

1.2.1 不连通孔喉中流体饱和度

压汞曲线中不能进汞的部分是由于毛管力的作用汞无法进入的微细孔喉，因此在油水渗流的过程这部分孔喉中的流体也无法参与流动，定义这部分流体为不连通孔喉中的流体，则其饱和度为：

Ss=100-SHgmax

(6)

式中，Ss—不连通孔喉中流体饱和度；SHgmax—最大进汞饱和度.

1.2.2 不连通孔喉中束缚水和残余油饱和度

根据润湿性计算的不连通孔喉中束缚水和残余油饱和度为：

(7)

(8)

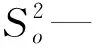
1.3 束缚水和残余油饱和度

岩心中束缚水和残余油饱和度为边界层和不连通孔喉中束缚水和残余油饱和度之和：

(9)

(10)

式中，Sor—残余油饱和度；Swc—束缚水饱和度.

2 渗透率损失程度

超低渗透油藏中由于孔喉比巨大，两相渗流过程中贾敏效应非常严重，导致油水相相对渗透率总和小于1.水驱油时，可动水占可动流体的比例由0增加到1的过程，是油相由连续相被切割成为非连续相，油滴由大到小并最终消失的过程，此过程中的贾敏效应程度先增大后减小.本文通过实验确定了3个特征点(油相端点、共渗点和水相端点)处的渗透率损失程度，通过平滑连接这3个点近似表征渗透率损失程度随含水饱和度的变化关系.

2.1 油相端点处渗透率损失程度

油相端点处为单相渗流，此时渗透率损失程度为0.

2.2 共渗点处渗透率损失程度

水驱油的过程中水会把油相切割为非连续相，非连续相的油滴数量增加，导致贾敏效应增强，渗透率损失程度加剧.随着含水饱和度的进一步增加，油滴的半径不断减小，其能通过的喉道不断增多，此时随着含水饱和度的增加渗透率损失程度减弱.因此，存在贾敏效应最严重点，即共渗点处，渗透率损失程度达到最大.由于气液的粘度差异巨大，液体更容易被气体切割形成非连续相，气驱水贾敏效应比水驱油更严重，用可测得的气驱水最终渗透率损失程度近似水驱油最大渗透率损失程度，通过对实验数据[14]进行拟合建立了共渗点处渗透率损失程度与气测渗透率的关系：

Rmax=-0.047 544lnK+0.778 31

(11)

式中，Rmax—共渗点处渗透率损失程度，小数；K—气测渗透率，10-3μm2，<1×10-3μm2.

2.3 水相端点处渗透率损失程度

水相端点值是残余油饱和度时水相相对渗透率.由于残余贾敏效应的对喉道的堵塞作用导致水相相对渗透率不能达到1，而退汞效率正是毛管力对汞捕获的结果，因此水相端点处渗透率的损失程度可用1-退汞效率We来近似表征.

2.4 渗透率损失程度

在已知3个特征点处的渗透率损失程度，通过圆滑连接这3个点得到渗透率损失程度随饱和度变化的图版(图1).通过对比10条实验和计算相对渗透率曲线发现，渗透率损失程度与含水饱和度满足：

(12)

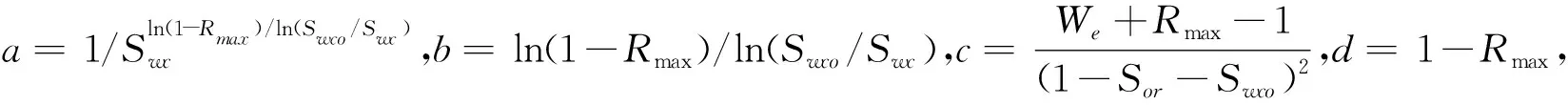
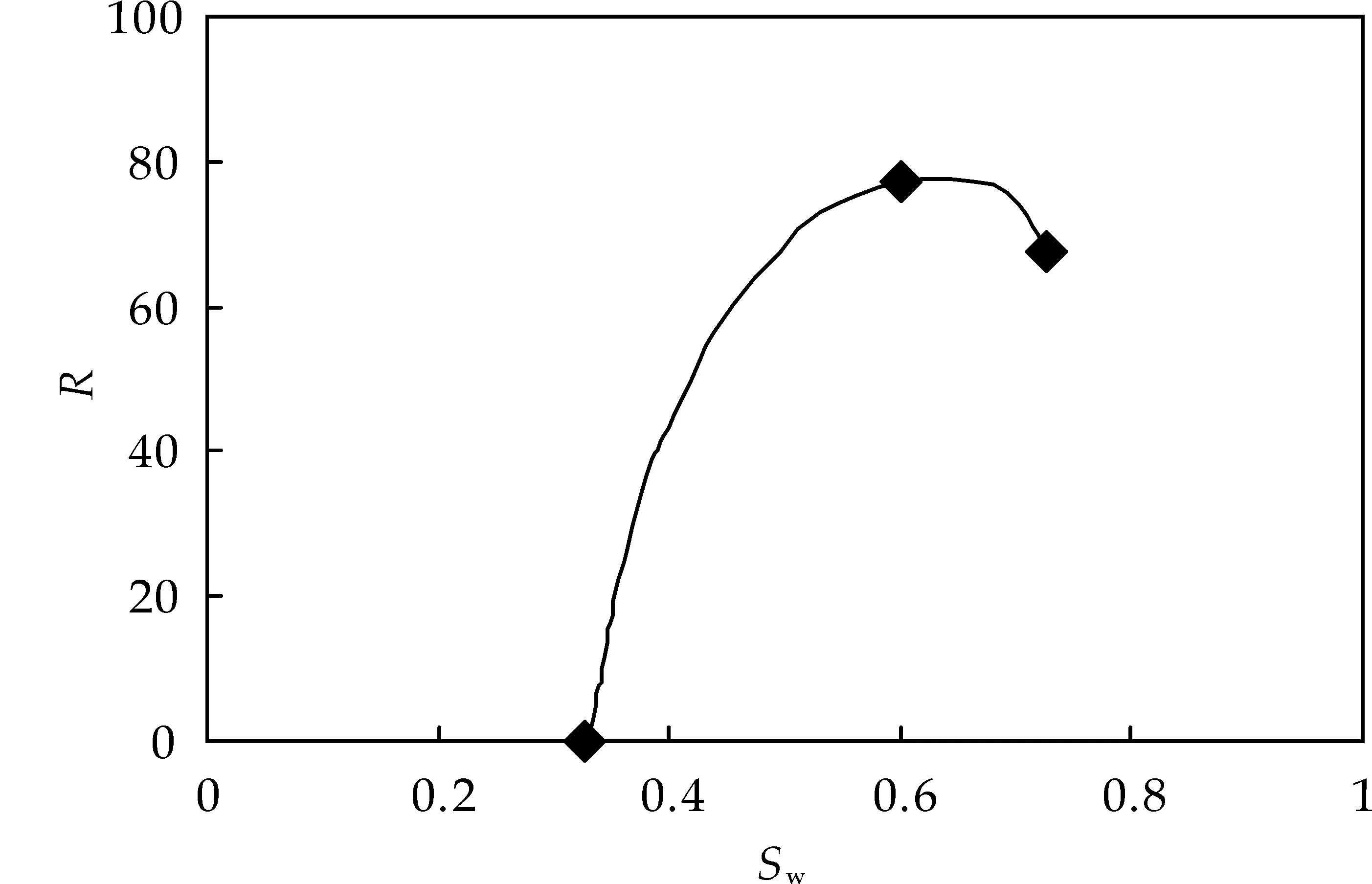
图1 渗透率损失程度与饱和度关系

3 相对渗透率计算模型

Brooks和Corey于1966年[4]提出的相对渗透率计算模型为：

(13)

(14)

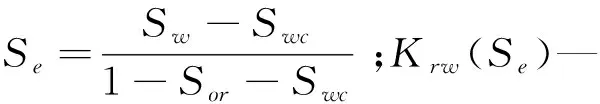
式(13)和(14)第一项为喉道迂曲度，但喉道迂曲度主要影响绝对渗透率，对相对渗透率影响较小，而贾敏效应对相对渗透率影响较大.因此本文忽略Brooks-Corey模型中的喉道迂曲度项，引入渗透率损失程度来考虑贾敏效应对渗流的影响.

边界层的作用结果导致有效流动半径减小：

r′=r-h

(15)

式中，r′—半径为r的微圆管中有效流动半径，μm.

因此毛管力随之增大，将汞气毛管力转化为油水毛管力：

(16)

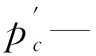
(17)

式中，pb，λ′—常数.

流动空间由(1-SHgmax～1)减小到(Swc～1-Sor)，对于亲水油藏，水驱油过程中，由于毛管力为动力，喉道半径越小毛管力越大，水优先进入小喉道，考虑边界层和贾敏效应的相对渗透率计算模型为：

(18)

(19)

4 模型验证

为了验证模型的可靠性，选择了孔隙度为12.7%，渗透率为0.673×10-3μm2润湿指数为0.2(弱亲水)的长庆超低渗透油藏岩心进行了压汞(图2)和相渗实验，相渗实验采用的原油粘度为1.5 mPa·s，水粘度为1 mPa·s.通过与Brooks-Corey模型对比发现(图3)，新模型有效的解决了无法计算束缚水和残余油饱和度及水相端点为1的问题，而且准确度更高.

图2 岩心压汞曲线

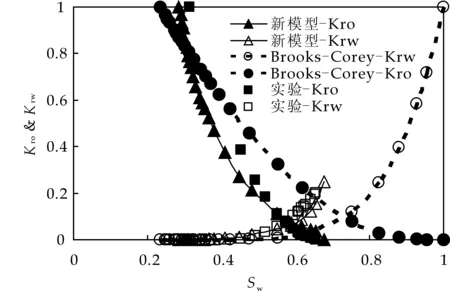
图3 Brooks-Corey，新模型 与实验结果对比

5 实例应用

通过修正的Brooks-Corey模型计算了长庆和大庆相同渗透率不同孔喉分布(图4)的超低渗透油田的相对渗透率曲线(图5)，假设油藏弱亲水(I=0.2).通过图5可以看出，由于储层渗透率相同，因此相渗曲线共渗点和水相端点值相等.但由于长庆油田大孔喉更多，两相区更宽，共渗点出现的更晚，导致长庆油田油相渗透率始终大于大庆油田，水相渗透率始终小于大庆油田.但是长庆油田在高含水段相对渗透率变化更剧烈，这是因为油藏亲水，水驱油过程中毛管力为动力，水先进入小喉道，最后进入大喉道.而大喉道对渗透率的贡献巨大，因此在高含水段长庆油田相渗曲线变化更剧烈.

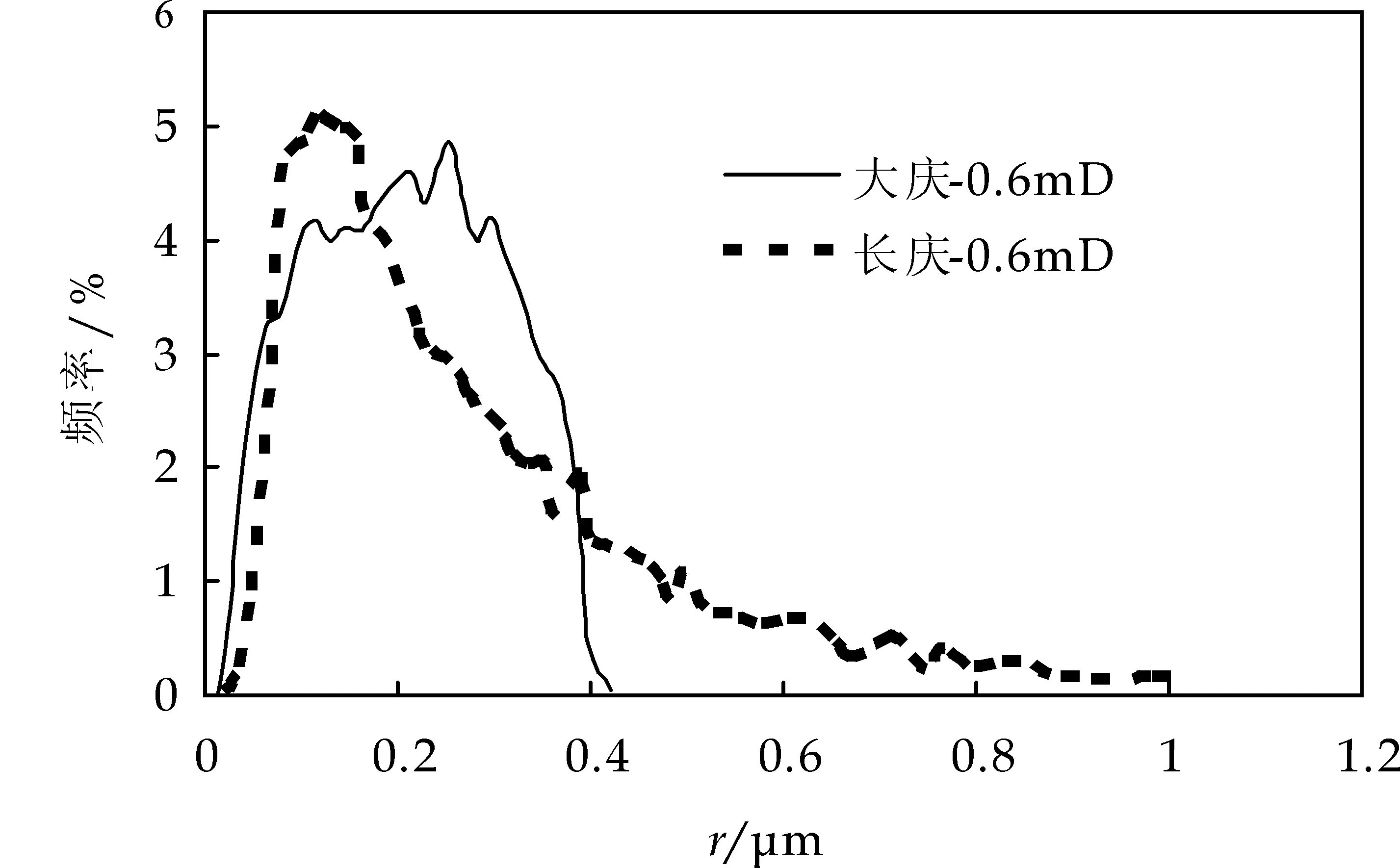
图4 大庆与长庆油田0.6 mD 岩心喉道半径分布

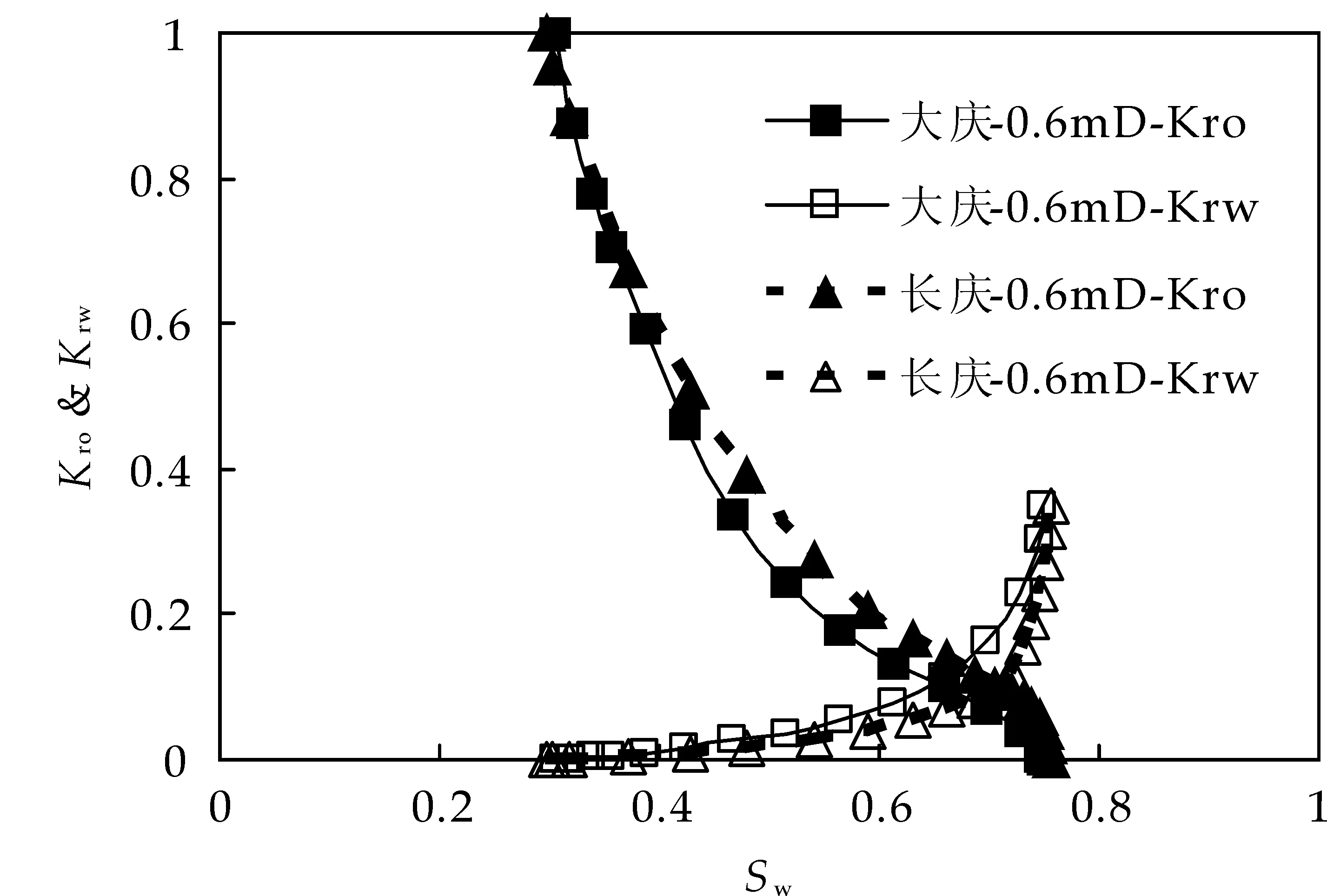
图5 大庆与长庆油田0.6mD 岩心相渗曲线

6 结论

(1)通过修正Brooks-Corey模型，建立了考虑微观孔喉分布的相对渗透率计算模型.经验证，新模型更加准确可靠.

(2)由于长庆油田孔喉分布范围更大，导致两相区更宽，共渗点出现的更晚，因此长庆油田的油相相对渗透率大于大庆油田，而且高含水段渗透率变化更剧烈.

[1] Burdine N.T.Relative permeability calculations from pore size distribution data[J].Journal of Petroleum Technology,1953,5(3):71-78.

[2] Corey A.T.The interrelation between gas and oil relative permeabilities[J].Producers Monthly,1954,19:38-41.

[3] Purcell W.R.Capillary pressures-their measurement using mercury and the calculation of permeability therefrom[J].Journal of Petroleum Technology,1949,1(2):39-48.

[4] Brooks R.H.,Corey A.T.Properties of porous media affecting fluid flow[J].Journal of the irrigation and drainage division,1966,6:61-88.

[5] Honarpour M.M.,Koederitz L.,Harvey A.H.Relative permeability of petroleum reservoirs[M].Florida:CRC Press,1986:19.

[6] 黄祥峰,张光明,郭俊磊,等.计算油藏相渗曲线的新方法及应用[J].石油地质与工程,2013,27(1):53-55.

[7] 吕新东,冯文光,杨 宇,等.利用动态数据计算相渗曲线的新方法[J].特种油气藏,2009,16(5):65-66.

[8] 戴胜群,付 波,洪秀娥,等.油藏综合相渗曲线拟合方法[J].油气藏评价与开发,2011,34(3):1-4.

[9] 李 洋,雷 群,刘先贵,等.微尺度下的非线性渗流特征[J].石油勘探与开发,2011,38(3):336-340.

[10] 李中锋,何顺利.低渗透储层原油边界层对渗流规律的影响[J].大庆石油地质与开发,2005,24(2):57-59.

[11] 徐绍良,岳湘安,侯吉瑞,等.边界层流体对低渗透油藏渗流特性的影响[J].西安石油大学学报(自然科学版),2007,22(2):26-28.

[12] 徐绍良,岳湘安.低速非线性流动特性的实验研究[J].中国石油大学学报(自然科学版),2007,31(5):60-63.

[13] 王正波,岳湘安,韩 冬,等.影响低渗透油藏低速非线性渗流的实验研究[J].矿物学报,2008,28(1):48-54.

[14] 唐 海,吕渐江,吕栋梁,等.致密低渗气藏水锁影响因素研究[J].西南石油大学学报(自然科学版),2009,31(4):91-94.