一类具logistic出生率的SIS传染病模型的全局稳定性
2014-06-27段彩霞廖新元
杜 鹏, 段彩霞, 廖新元
(南华大学 数理学院, 湖南 衡阳 421001)
0 引言
用常微分方程来分析、研究传染病的扩散与控制在理论和实践中都有广泛应用.在1932年Kermack和McKendrick针对康复后仍不具有免疫力的传染病提出了SIS模型[1]后,很多学者在此基础上建立了传染病模型[2-10],并研究了人口总数变化的SIS模型[2]. 针对长时间流行的传染病种群数量在不断变化这一事实,本文提出具logistic出生率的SIS模型[11-15],即:
(1)
其中S(t)、I(t)分别表示易感染者、感染者在t时刻的总数,K>0为种群的最大容量,λ>0为种群的内禀增长率,β≥0为传染率,γ>0为恢复率,μ>0为自然死亡率.
对系统(1)作变换dt=K(S+I)dw,仍然记dw为dt,得到系统(2):
(2)
基于系统的生物意义,在区域G={(S,I)|S≥0,I≥0}中研究问题.
1 平衡点的存在性
定理1系统(2)在G上总存在无病平衡点E0(0,0),E1(K,0);当
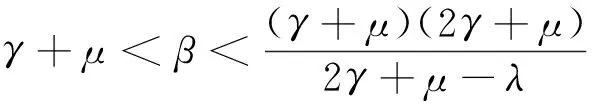
2 解的有界性
对于系统(2)的解的有界性方面我们有下列结论.
定理2系统(2)的所有正解最终有界.
证明:令V(t)=S(t)+I(t)则沿着系统(1)的全导数为:

3 无病平衡点的稳定性
定理3[11]当β<γ+μ时,无病平衡点E1(K,0)局部渐近稳定.
证明:系统(2)在平衡点E1(K,0)处的雅可比矩阵为
所以特征方程为:
|aE-J1|=(a+K2λ)(a-K2(β-γ-μ))=0
故特征根为a1=-K2λ,a2=K2(β-γ-μ). 当β<γ+μ时,a1<0,a2<0,因此无病平衡点E1(K,0)局部渐近稳定.
4 地方病平衡点的稳定性
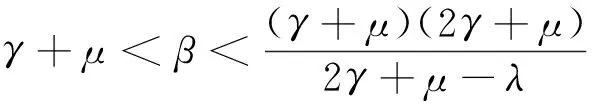
证明:系统(2)在E2(S*,I*)处的雅可比矩阵为,
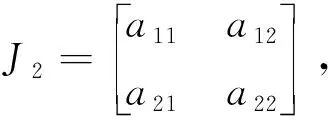
a22=KS*(γ+μ-β)
则相应的特征方程为
|aE-J2|=
a2-(a11+a22)a+a11a22-a21a12=
a2+pa+q=0
其中
3βμ+λβ+2μ2)=
(γ+μ)2+3γ(γ+μ)+β(β-5γ-2μ))>
所以两个特征根均为负值,故平衡点E2(S*,I*)局部稳定.
5 零平衡点的稳定性
在E0(0,0)处系统(2)的雅可比矩阵为零,上述方法无法判定其稳定性,故用特殊方向和法域来判定E0(0,0)领域内的轨线结构.
作极坐标变换S=Rcosθ,I=Rsinθ,系统(2)变为:
其中
H(θ)=K(λcosθ(sinθ+cosθ)2+γsinθcosθ(sinθ+cosθ)+βsinθcosθ(sinθ-cosθ)-(γ+μ)sin2θ(sinθ+cosθ)),
G(θ)=Ksinθ(sinθ+cosθ)((β-λ-γ-μ)cosθ-(γ+λ)sinθ).
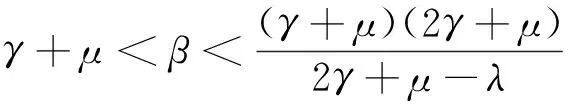

(1)当β<γ+μ时,((β-λ-γ-μ)cosθ-(γ+λ)sinθ)≠0,sinθ+cosθ≠0示性方程G(θ)=0有唯一解θ=0,H(0)=λK≠0,故θ=0为特殊方向.在θ逆时针经过θ=0时,H(0)G(θ)由正变负,故角域N1={(R,θ)|0≤R≪1,|θ|≪ε}为第Ⅱ型法域,且
则在N1={(R,θ)|0≤R≪1,|θ|≪ε}内轨线的走向如图1所示.

图1 轨线的走向
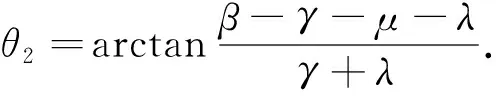
H(θ2)=Kcos3θ2(λ(tanθ2+1)2+βtanθ2(tanθ2-1)+γtanθ2(tanθ2+1)-(γ+μ)tan2θ2(tanθ2+1))=Kcos3θ2(-(γ+μ)tan3θ2+(λ+β+γ)tan2θ2+(2λ-β-μ)tanθ2+λ)
设x=tanθ,f(x)=-(γ+μ)x3+(λ+β+γ)x2+(2λ-β-μ)x+λ,则f′(x)=-3(γ+μ)x2+2(λ+β+γ)x+(2λ-β-μ),
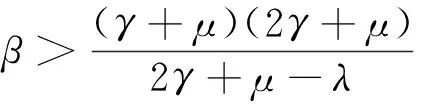

轨线在角域N2的走向如图3所示.

轨线在角域N2的走向如图3所示.
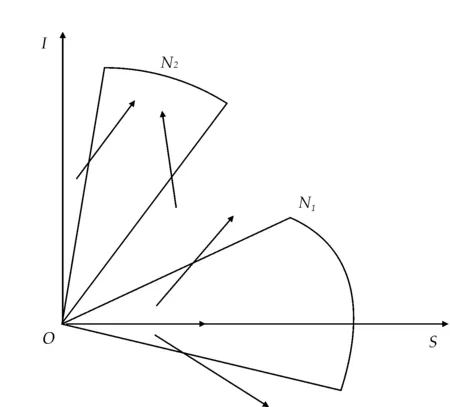
图2 轨线的走向

图3 轨线的走向
6 闭轨的不存在性
Bendixson-Dulac判别法[3]:若在单连通域G内存在函数B(x,y)∈C1(G)使
且不在G的任意子区域内恒为零,则原系统不存在全部位于G内的闭轨线和具有有限个奇点的奇异闭轨线.
定理6系统(2)不存在全部位于G={(S,I)|S≥0,I≥0}内的闭轨线和具有有限个奇点的奇异闭轨线.
证明:在G内取Dulac函数
恒负,由Bendixson-Dulac判别法知,系统(2)不存在全部位于G内的闭轨线和具有有限个奇点的奇异闭轨线.
7 结论

8 数值模拟

[1] Kermack W O,Mc Kendrick A G.Contribution to the mathematical theory of epidemics[J].Proc.Roy.Soc.,1932,138(1):55-83.
[2] Li J,Ma Z.Qualitative analyses of SIS epidemic model with vaccination varying total population size[J].Mathematical and Computer Modeling,2002,35:1 235-1 243.
[3] Su Ying,Wei Junjie,Shi Junping.Hopf bifurcation in a diffusive logistic equation with mixed delayed and instantaneous density dependence[J].Dynamics and Differential Equations,2012,24:897-925.
[4] Shengle Fang,Minghui Jiang.Stability and hopf bifurcation for a regulated logistic growth model with discrete and distributed delays[J].Communications in Nonlinear Science and Numerical Simulation,2009,14(12):4 292-4 303.
[5] Huaixing Lia,Yoshiaki Muroyab,Yukihiko Nakatab,et al.Global stability of nonautonomous logistic equations with a piecewise constant delay[J].Nonlinear Dynamics,2010,11(3):2 115-2 126.
[6] Shanshan Chen,Junping Shi.Stability and hopf bifurcation in a diffusive logistic population model with nonlocal delay effect[J].Journal of Differential Equations,2012,253(12):3 440-3 470.
[7] 马知恩.传染病动力学的数学建模与研究[M].北京:科学出版社,2004:116-147.
[8] 陈兰荪,陈 键.非线性生物动力系统[M].北京:科学出版社,1993:111-123.
[9] 徐为坚.具有种群Logistic增长饱和传染率的SIS模型的稳定性和Hopf分支[J].数学物理学报,2008,28(3):578-584.
[10] 胡新利.具有Logistic出生率和饱和接触率SIR模型的全局分析[J].纺织高校基础科学学报,2011,24(2):209-211.
[11] 赵仕杰,李大普.一种群Logistic增长及非线性发生率的时滞SIS传染病模型的稳定性与Hopf分支[J].广西科学院学报,2011,27(1):6-9.
[12] 王晓燕,杨俊元.具有Logistic增长和年龄结构的SIS模型[J].数学的实践与认识,2007,37(15):99-103.
[13] 杨俊元,郑 福,王晓燕,等.一类具有Logistic增长和病程的SIR模型[J].数学的实践与认识,2009,39(11):120-124.
[14] 胡新利,孙法国,王彩霞.具有饱和接触率和垂直感染的SIR 模型全局分析[J].纺织高校基础科学学报,2010,23(1):120-122.
[15] 何莲花.一阶微分方程的周期解[J].贵州师范大学学报(自然科学版),2011,29(3):100-102.
