基于度量值的球形检测算法改进
2014-06-27朱国晖
朱国晖, 张 磊
(西安邮电大学 通信与信息工程学院, 陕西 西安 710121)
0 引言
长期演进(Long Term Evolution,LTE)是一种准4G的无线接入技术,支持多输入多输出(Multiple-Input Multiple-Output,MIMO)技术,可以在20 Mb/s频谱带宽下提供最高100 Mb/s的峰值速率,拥有很高的频谱利用率[1].但是,无线信道的不确定性,直接导致接收端收到的信号是发射端多路信号的叠加.如何使得接收端能够准确译码,检测算法起着至关重要的作用.
最大似然(Maximum Likelihood,ML)检测[2]作为最优检测算法,在带来高性能检测的同时,其复杂度也随着发射天线数目和调制星座阶数成指数增长.早期提出的次优检测算法包括有以迫零检测算法[3]、最小均方误差算法[4]为代表的线性检测算法;以串行干扰消除检测算法[5]和并行干扰删除检测算法[6]为代表的非线性检测算法.这些算法虽然在复杂度上有所降低,但检测性能成为它们在实际应用中的瓶颈.球形检测算法(Sphere Detection,SD)[7]作为ML 检测的一种改进方法,在降低计算复杂度的同时,可实现ML的性能解调.
目前,对于球形检测算法的研究主要从两个方面入手,其一为初始半径设置,其二为搜索策略.在改进初始半径方面,文献[8]提出了一种基于误比特率(Bit Error Rate ,BER)的半径收敛方案.但该方法无法确保半径内一定有解,需要设定空解返回策略.在搜索策略方面,文献[9]是对深度优先算法的改进和实现,采用单一树的方式进行搜索,但依然保留了计算量较大的问题.
针对上述问题,本文拟提出一种基于度量值的球形检测(Metric Spherical Detection,MSD)算法,在深度优先搜索树的基础上引入度量值的概念,即将球形检测过程转化为基于加权值的最短路径搜索问题.
1 系统模型
对于MIMO系统采用NT根发射天线,NR根接收天线,NT≤NR,信道状态为平坦瑞利衰落,系统收发天线模型如图1所示.

图1 MIMO系统模型
由图1可知,通过采用垂直分层空时编码(Vertical Bell Labs Layered Space-Time, V_BLAST)结构[10],接收端每路信号之间相互独立,并且接收端矢量y是各个发射天线经过平坦衰落信道后的总合.LTE系统的信号模型为
y=Hx+N,
其中
y=[y1,y2,…,yNR]T,
x=[x1,x2,…,xNT]T,
N=[N1,N2,…,NR]T,
H=[hi,1,hi,2,…,hi,j]T,
分别对应为接收信号矢量、发射信号矢量、加性高斯白噪声矢量和信道矩阵.H是复数域上NT×NR矩阵,元素hij(i=1,…,NT,j=1,…,NR)表示第i根发射天线到第j根接收天线之间的信道响应.各元素服从均值为0,δ2方差为δ2的高斯分布.
假设接收端已知信道状态信息,进行最大似然检测得
2 球形检测算法
球形检测算法的基本思想是在以矢量x为球心,以d为半径的m维球内搜索符合条件的结点.其中
d2≥‖y-Hx‖2
(1)
通过选择初始半径、设定搜索策略来缩小搜索范围.减少访问节点数,从而降低了计算的复杂度.
对信道矩阵H进行QR分解得
其中Q为NR×NR的酉矩阵,R为NT×NT的上三角矩阵,则式(1)相当于
另设
由于R为上三角矩阵,所以有
展开可得
rm-1,mxm-rm-1,m-1xm‖2+…≤C2
(2)
由上三角矩阵的特点,可得
求解可得xm的取值范围
另记
(3)
将xm代入上式,可得
依次类推,通过xm,xm-1,…,xi+1即可得到信号xi,最终获得目标矢量x.
3 基于度量值的球形检测算法
3.1 初始半径
传统球形检测算法的初始半径C通常设置为∞,初始搜索阶段半径较大,检测结点多,相对效率很低.通过工程经验获得初始半径公式为
C2=αnδ2,
其中α是初始半径系数,n为两倍的发射天线数目,δ2为噪声方差.在低信噪比的情况下,搜索半径会随着噪声功率的增大而增大,使得计算复杂度也随之增加.
由于最终的检测信号是一个多维空间向量,因此可以从根结点开始,对每层度量值进行升序排列,依次选取最小度量值一直向下扩展,直到叶子结点,该叶子结点的路径
即为初始半径的目标矢量.
设定度量值:
其中Δyj,k表示搜索树中第j层第k个结点的度量值.其中j的取值n,n-1,…,1,而k的取值受到码本更新的影响,每次的获得可通过k=length()函数来获得.
由(2)式可得度量值和半径的关系
(4)
i=n,n-1,…,1
对每层度量值进行升序排列,取Δym,1作为最优度量值,由式(3)可知,每层的半径为
通过递归相加,可得
又因为
整理得初始半径
由于半径是通过最小度量值计算所得,通过文献[11]可知,即使该矢量不是最大似然检测信号,也一定是一个较优的搜索半径,并且在保证半径快速收敛的同时,该半径范围内必然会存在至少一个解,使得搜索过程不会出现空解,因此不用为此设置专门的返回策略.
3.2 搜索策略
从第N层取第一个结点作为根结点,沿着某一条路径一直向下展,通过更新的码本计算出各个结点的度量值,根据公式(4)判断,如果
φ(Δyj,k)>C2
则重新选择一条路径向下扩展,一直扩展到叶子结点.如果
φ(Δyj,k) 则保留该结点路径到存储列表,同时更新搜索半径,重复该过程直到跳出循环. 算法流程如下: update codebook; (2) tmp=tmp+Δyi,j (3) if tmp>C2,j=j+1,goto(2) ifj>length(ind(k)),i=i+1,goto(2) ifi>nbreak (4) elseif tmp ifi<1 savex (5)C2=tmp,goto(1) 作为遍历性搜索算法,传统球形检测需要遍访限制区域内的每个结点.如果前面k层都符合约束条件,直到k+1层才发现不符合,我们将k+1层以后仍然访问的结点称为坏点.当信噪比较低时,搜索半径不能快速收敛,导致坏点增多,这样造成大量的计算浪费.通过采用上述的搜索策略算法,在前m(m 采用4×4的MIMO系统,调制方式为4QAM,传输信道为平坦瑞利衰落信道,噪声为高斯白噪声.设置发射端天线功率为1,在传输过程中,接收端能估计出信道矩阵. 分别对最大似然检测算法(ML)、传统球形检测算法(SD)和基于度量值的球形检测算法(MSD)在不同信噪比时的误码率和算法的复杂度进行了仿真对比. 关于误码率的仿真对比结果如图2所示. 图2 误码率曲线 可以看出,MSD算法与ML算法的性能十分接近.随着信噪比的增加,MSD算法也较传统的SD算法在误码率上有所降低. 三种算法在计算量上的对比结果如图3所示. 因为ML算法需要遍历全部结点,故计算量非常大.由于MSD算法所得半径是较优的搜索半径,在开始的结点访问个数相对于传统的SD算法降低了一个数量级. 图3 访问结点个数曲线 仿真时间对比结果如图4所示. 图4 仿真时间曲线 由图4可以看出,MSD检测算法在减小复杂度方面有着明显的优势.在低信噪比的情况下,MSD算法仿真时间有明显的下降趋势.这取决于基于最小度量的初始半径快速收敛的结果. 基于度量值的球形检测算法能够快速找到一个较优的初始半径,并且随着信噪比的增加,基于最小度量值的初始半径越接近于最大似然半径.在不用担心空解的情况下,半径越小,该算法的搜索策略就能更早的辨别出坏点,从而提前终止无效遍历过程,降低算法的计算量. [1] 孙全兵.TD-LTE技术在移动互联网中的应用研究[J].计算机光盘软件与应用,2012,7(14):126-127. [2] Kim J S,Moon S H,Lee Inkyu.A new reduced complexity ML detection scheme for MIMO systems[J].IEEE Transactions on Commucations,2010,58(4):1 302-1 310. [3] Wiesel A,Eldar Y C,Shamai S.Zero-forcing precoding and generalized inverses[J].IEEE Transactions on Signal Processing,2008,56(9):4 409-4 418. [4] 汪晋宽,贾利琴,刘志刚,等.基于SP子空间跟踪的修正的MMSE多用户检测方法[J].东北大学学报,2006,27(4):382-385. [5] Liu Tsung Hsien.Some results for the fast MMSE-SIC detection in spatially multiplexed MIMO systems[J].IEEE Transactions on Wireless Communications,2009,8(11):5 443-5 448. [6] Studer C Fateh S,Seethaler D.ASIC Im-plementation of soft-input soft-output MIMO detection using MMSE parallel interference cancellation[J].IEEE Journal of Solid-State Circuits,2011,46(7):1 754-1 765. [7] Vikalo H,Hassibi B.On the sphere deco-ding algorithm[J].IEEE Transactions on Signal Processing,2005,53(8):2 806-2 818. [8] Lai Kuei Chiang,Huang Cheng Chieh,Jia Jiun Jie.Variation of the fixed-complexity sphere decoder[J].IEEE Communications Letters,2011,15(9):1 001-1 003. [9] Burg A,Borgmann M,Bolcskei H.VLSI implementation of MIMO detection using the sphere decoding algorithm[J].IEEE Journal of Solid-State Circuits,2005,40(7):1 566-1 577. [10] 战金龙,卢光跃,姜 晖.STBC-VBLAST系统发射天线选择算法研究[J].西安邮电学院学报,2011,16(2):13-16. [11] 熊 丹,蔡世杰,周春晖,等.一种低复杂度的球形检测算法[J].移动通信,2011,35(3):126-130.
4 仿真结果与分析
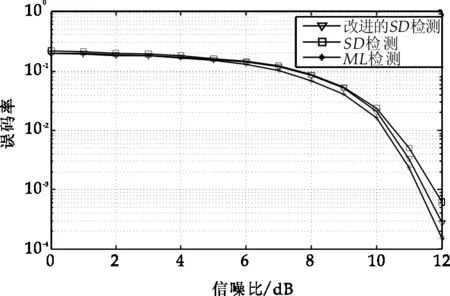


5 结束语
