结构实模态参数的高阶灵敏度算法

张 淼

（长春工程学院理学院，长春 130012）

结构实模态参数的高阶灵敏度算法

张 淼

（长春工程学院理学院，长春 130012）

针对对称单频系统，讨论其无阻尼实模态参数的高阶灵敏度分析的算法。建立了计算模态灵敏度的算法流程，通过该流程获得了一、二阶模态灵敏度系数的控制方程，即可同时获得固有频率及实模态一、二阶灵敏度。由于算法的可操作性强，更高阶灵敏度的精确值可依次获得。

模态参数；高阶灵敏度；灵敏度系数；实模态；对称系统

0 引言

一个结构的动力特性可以用它的模态参数加以完整的描述。这些模态参数可以从结构模型已知的质量、刚度和阻尼矩阵导出，也可以用测量出来的该结构的频响函数导出。模态参数可分为实模态参数和复模态参数。实模态参数包括无阻尼固有频率、阻尼比及实模态，复模态参数包括极点（复频率）及复模态。

灵敏度分析是指考虑设计参数对结构的影响，把结构性质矩阵和模态参数等看作是关于设计参数的函数，求它们各自关于设计参数向量的梯度［1］，统称为灵敏度信息。灵敏度信息主要依赖初始状态下的结构参数及设计参数，更能直观地反应结构对设计参数的敏感性，同时具有良好的数学及物理意义，因此成为近年来结构动力修改及分析的主要研究方向之一［2－3］。

针对模态的灵敏度分析算法可分成直接法和模态法两大类型。两种方法都需对特征方程求导得到支配方程，它的系数矩阵至少降一个秩，直接法是对支配方程的系数矩阵进行非奇异化处理，从而直接求解模态灵敏度。而模态法是指首先构建完全的特征空间基底，在支配方程中将模态灵敏度写成基底的某一线性组合形式（组合系数待定），最后利用各种技术来计算组合系数，从而确定模态灵敏度。文献［4］给出了计算各种振系模态的一阶灵敏度的统一算法，而针对频率及模态的高阶灵敏度算法还很少在现有文献中出现，即使工程中应用高阶灵敏度时也都做了一定程度的简化［5－6］。

本文主要研究对称单频系统的固有频率及实模态的高阶灵敏度算法。

1 实模态参数的一阶灵敏度

对N自由度的线性离散振动系统的运动方程为：

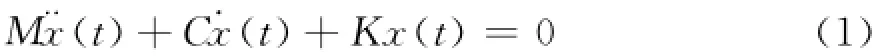
式中M，C和K∈RN×N分别为对称系统的质量、阻尼和刚度矩阵。

结构有限元分析时，做拉普拉斯变换x（t）＝uewt＝ueiωt（w＝iω）代入式（1）可得（w2Mu＋wCu＋Ku）ewt＝0。令C＝0，则无阻尼固有频率与实模态对（ω2i，ui）（i＝1，2，…，N，w2＝－ω2），满足特征方程

设每个实模态的正则化系数为ai，即

记aiui＝φi和λi＝－ω2i（i＝1，2，…，N），则式（2）改写为

实际上特征方程（4）是关于矩阵M和K的广义特征问题。设Φ＝［φ1，…，φN］为无阻尼正则实模态矩阵，对单频对称系统而言，实模态关于矩阵M和K是加权正交的［7］。因此，

再由式（3），可得

代入式（4），可得

引入设计参数向量b＝（b1，…，bq）T，相应的特征方程（4）应为K（b）φ（b）＋λ（b）M（b）φ（b）＝0，为了讨论方便，以下我们仍记为如式（4）的形式。

考虑灵敏度问题，定义第i个实模态向量φi∈RN的灵敏度矩阵为

对单频（无阻尼）系统来说，由于全部固有频率所对应的实模态向量φk（k＝1，…，N）无关，可作为矩阵广义特征空间的基底，也可作为N维空间的基底，因此N维实模态向量的一阶灵敏度φi，j（j＝1，…，q）一定可在实模态空间内表示为基底的某一线性组合，即

将式（4）两边对第j个参数bj求导得

整理式（7）得实模态灵敏度φi，j的支配方程为

将式（7）代入支配方程，并左乘ΦT

用单频系统实模态向量之间的规范正交化关系式（5）和式（6）解耦支配方程，即可析出模态灵敏度系数的控制方程如下

首先观察灵敏度系数的控制方程组中第i个方程为

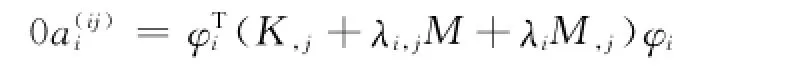
由模态灵敏度系数的控制方程的解必然存在，不会出现矛盾方程，因此上式右端恒为0，故可解得

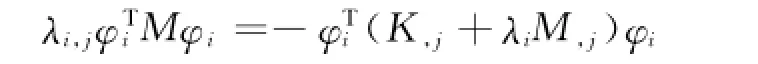
根据规范化条件φTiMφi＝1，可解得所有单频的灵敏度为

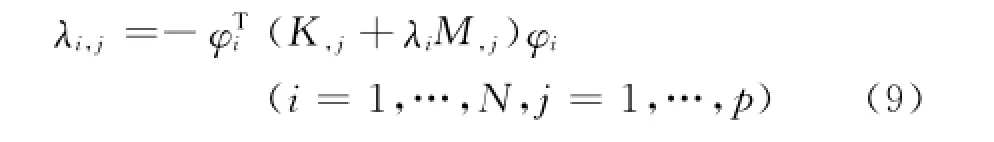
其次，由第i个以外的方程可解得模态灵敏度系数为

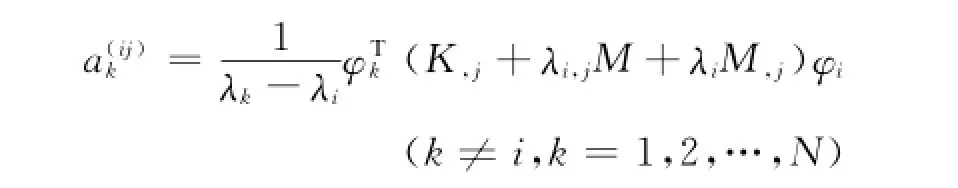
同样地，根据正交化条件φTkMφi（k≠i），可简化为

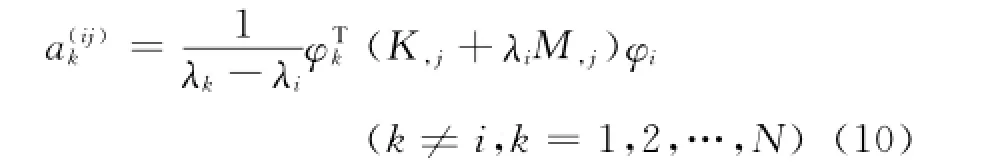
由式（10）和式（11）即获得全部模态灵敏度系数，代入式（7）即可获得各实模态一阶灵敏度。

2 实模态参数的二阶灵敏度

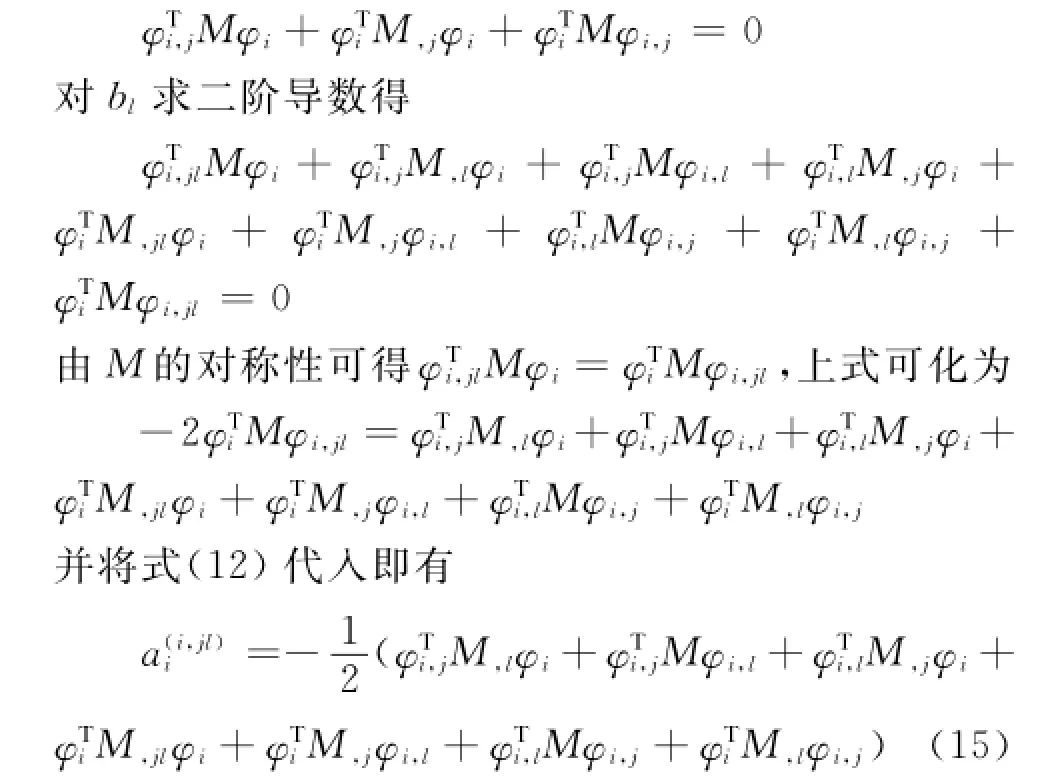
由式（14）和式（15）即获得全部二阶模态灵敏度系数，代入式（12）即可获得各实模态的二阶灵敏度。类似地，固有频率及实模态的更高阶灵敏度可依次求解。

3 结语

由上文的讨论可知，这种算法实际上是一个流程，在用Matlab等软件实现固有频率的一、二阶灵敏度（见式（9）和式（13））及实模态的一、二阶灵敏度（见式（7）和式（12））时，必须注意它们所使用的特征方程形式，有时在工程中，由于不同的实际需要所建立的特征方程形式大同小异，那么就要特别地依据本文所建立的算法流程，对式（9）、（13）、（7）、（12）等公式进行调整和修正，才能得到正确及可靠的结果。

［1］于澜，张任，乐明锋，等.模态参数的灵敏度分析在结构工程领域中的应用［J］.长春工程学院学报：自然科学版，2012，13（3）：1－3.

［2］张淼，于澜，鞠伟.基于松驰技术的重频密频结构模态灵敏度分析［J］.合肥工业大学学报：自然科学版，2012，35（12）：1605－1609.

［3］于澜，张淼，鞠伟，等.非保守系统复模态的规范正交性及其应用［J］.华南师范大学学报：自然科学版，2013，45（4）：21－24.

［4］张淼，鞠伟.计算各种振系模态灵敏度的统一算法［J］.长春工程学院学报：自然科学版，2012，13（4）：119－122.

［5］杨佑发，赵忠华，徐典.基于改进模态参数灵敏度法的结构损伤识别研究［J］.地震工程与工程振动，2011，31（1）：95－100.

［6］薛松涛，钱宇音，陈荣，等.采用二阶频率灵敏度的损伤识别和试验［J］.同济大学学报，2003，31（3）：263－267.

［7］张淼，陈庆文.两种常见的状态方程及其特征向量的正交性［J］.长春工程学院学报：自然科学版，2011，12（2）：122－125.

Higher－order sensitivity algorithm for real modal parameters of structures

ZHANG Miao
（School of Science，Changchun Institute of Technology，Changchun130012，China）

As for symmetric single－frequency system，a discussion on higher－order sensitivity algorithm for undamped real modal parameters is given in this paper.An algorithm process is provided for computing the mode sensitivity.The controlling equations to sensitivity coefficients of the first and second－order mode sensitivities are obtained.Then the natural frequency and the first and second－order real mode sensitivities are obtained immediately.Due to the superior of operation，the more higher－order sensitivities of mode can be obtained analogously.

mode parameter；higher－order sensitivity；sensitivity coefficient；real mode；symmetric system

O32

：A

：1009－8984（2014）01－0122－04

10.3969／j.issn.1009－8984.2014.01.031

2013－10－28

吉林省自然科学基金资助项目（201215115）

张淼（1972－），男（汉），长春，博士，副教授

主要研究结构优化及振动控制。