模糊PID控制在磁悬浮系统中的应用

宋荣荣，马卫华

(1.西南民族大学计算机科学与技术学院，成都 610041; 2.西南交通大学牵引动力国家重点实验室，成都 610031)

模糊PID控制在磁悬浮系统中的应用

宋荣荣1，马卫华2

(1.西南民族大学计算机科学与技术学院，成都 610041; 2.西南交通大学牵引动力国家重点实验室，成都 610031)

基于模糊控制的思想，建立以悬浮系统为对象的数学模型，根据悬浮系统自身特点并结合实际经验，找出输入变量误差E和误差变化率EC与PID的3个参数之间的模糊关系，制定模糊控制规则，设计了一种模糊自整定PID控制器。该控制策略的优点是能在悬浮系统工作时，对PID参数进行在线调节，以适应轨道不平顺的变化，使控制器跟踪精度高，响应速度快，鲁棒性好。利用Matlab中Fuzzy和M函数的有机结合，通过仿真验证了模糊自整定PID控制系统的可行性。结果表明:与传统的PID控制器相比，该方法能够对轨道的正弦波扰动和方波扰动实现更有效的跟踪，对外加干扰具有更强的抑制能力。为解决轨道不平顺问题提供了一种思路。

轨道不平顺;磁悬浮系统;模糊PID控制;Matlab仿真

在磁悬浮列车行驶过程中，轨道不平顺是影响悬浮性能的一个重要方面。有效克服轨道干扰是提高悬浮控制系统性能的一个重要因素［1］。从列车运行的安全性和乘客乘坐的舒适性两方面进行考虑，悬浮系统需能跟踪轨道表面的变化，如弯道、坡道等;对由轨道表面的不平整带来的低频和高频振动不敏感;同时还应该能有效克服由于车辆负载变化带来的扰动。目前的控制算法大多是以悬浮间隙作为位置信号，并结合电磁铁的加速度和线圈的电流等信号进行传统的PID控制［2－3］。实践证明:这种控制方法在克服轨道不平顺带来的影响方面效果并不理想。目前，很多国内外专家学者采用模糊控制的方法提高磁悬浮系统抗干扰的能力［4－10］。

模糊控制是近年来发展起来的一种新型控制方法［4］。其优点是无需受控对象的精确数学模型，它根据人工控制规则组织控制决策表，然后由该表决定控制量的大小。将模糊控制和PID控制器两者结合，扬长避短，得到的这种Fuzzy－PID复合型控制器既具有模糊控制灵活性和适应性强的优点，又具有PID控制精度高的特点，对单磁铁悬浮系统具有良好的控制效果，是近年来十分热门的研究课题［5－10］。

本文首先建立单电磁铁悬浮系统的数学模型，然后设计了一个模糊－PID复合型控制器。其主要思想是以误差和误差变化率作为输入，利用模糊控制规则，在不同时刻对PID参数进行自调整。基于Matlab软件的仿真结果表明:与传统的PID控制器相比，该控制器对轨道干扰和负载扰动具有更好的抑制效果。

1 悬浮系统模型

单电磁铁悬浮系统结构如图1所示。假设电磁铁不仅在垂直方向运动，还沿轨道以速度V运行。图1中:绝对气隙z(t)为磁极表面与绝对参考平面的距离;h(t)为轨道面与绝对参考平面的距离;相对气隙c(t)为磁极表面与轨道面的气隙;加速度计所测得的输出为加速度¨z(t);气隙传感器测得的输出为相对气隙c(t);i(t)为电流互感器测得的控制线圈电流;u(t)为绕组回路的电压。

图1 单电磁铁悬浮系统结构

设N为电磁铁线圈的匝数，A为磁极面积，R为线圈的电阻，μ0为空气磁导率，mg为电磁铁重力，F(i，c)为悬浮电磁力，fd(t)为外界干扰力。

在分析单电磁铁悬浮系统的动力学模型时，假设［11］:①忽略漏磁的影响;②忽略磁铁芯和导轨中的磁阻，磁势均匀降落在气隙c(t)上;③电磁铁仅有垂直方向上的移动，其他方向受限无运动。

根据电磁学和动力学理论，得到基于绝对参考平面的单电磁铁动态模型方程:

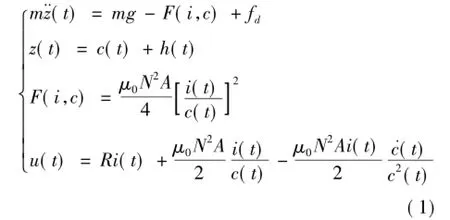
其中，平衡点的边界条件为:

2 模糊PID控制器的设计

模糊PID控制器的关键技术是找出误差E和误差变化率EC与PID的3个参数之间的模糊关系。根据确定的模糊控制规则对PID的3个参数进行在线调整，满足不同的E和EC对3个参数的要求，控制结构如图2所示。

图2 模糊PID控制结构

2.1 传统PID控制器的参数设定

对系统(2)增加一个状态变量∫Δc(t)dt，以电流为控制变量，得到开环系统的状态方程:

比较闭环特征方程(4)和期望的闭环传递函数(5)，可求得参数Kp=19 638.65，KI=603 880.52，KD=215.68。

2.2 各变量隶属函数的确定

以E和EC为输入语言变量，以Δkp，Δki和Δkd为输出语言变量。定义E和EC的模糊集均为{NB，NM，NS，ZO，PS，PM，PB}，控制量Δkp、Δki和Δkd的模糊集均为{NB，NM，NS，ZO，PS，PM，PB}。各变量的隶属函数曲线分别如图3～7所示。

图3 变量E的隶属函数

图4 变量EC的隶属函数

图5 变量Δkp的隶属函数

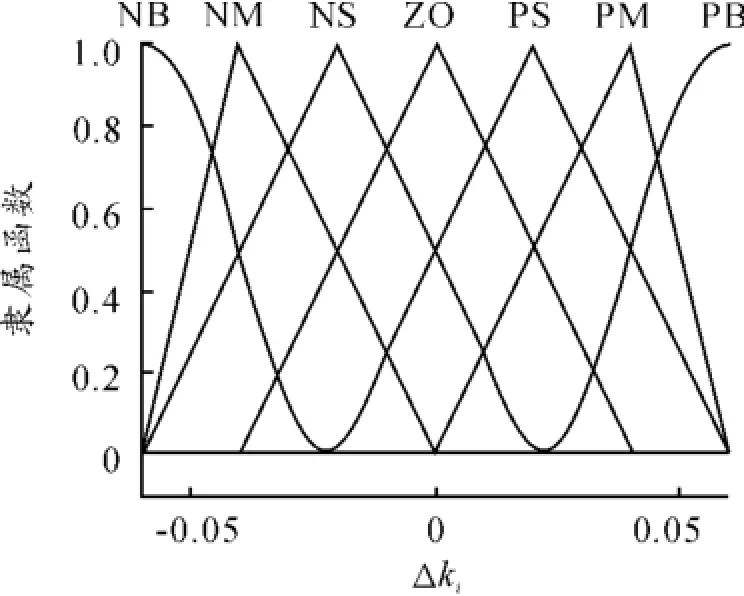
图6 变量Δki的隶属函数

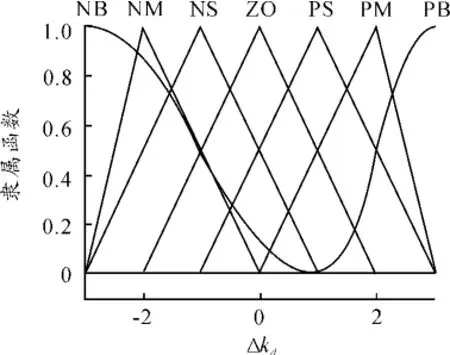
图7 变量Δkd的隶属函数

2.3 模糊控制规则

模糊控制规则是模糊控制器设计的核心内容。根据单电磁铁悬浮系统的特点与专家经验，通过分析大量成功的控制策略经验，制定模糊控制规则。制定的原则主要有:

1)仿真开始时，减少积分作用以防止饱和;仿真快结束时，增大积分作用以减少系统等稳态误差。

2)误差偏大时，增大比例作用以增加响应速度;误差偏小时，增大积分作用以保证系统稳定。

3)误差变化率偏大时，减少微分作用;误差变化率偏小时，增大微分作用。

采用模糊规则“IF A AND B THEN C”形式制定。由于2个输入变量各有7个语言值，因此分别建立Δkp，Δki和Δkd的49条模糊规则，见表1～3。

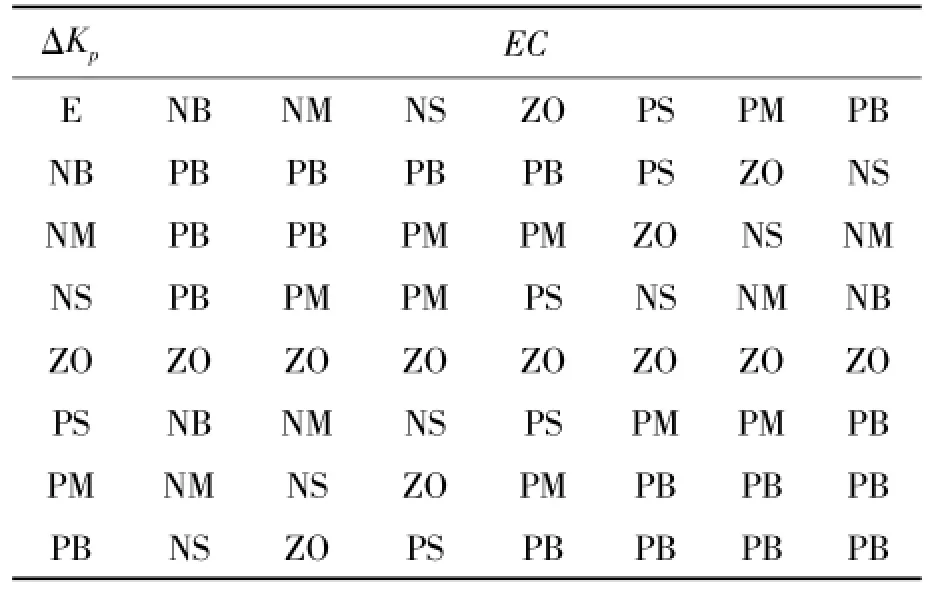
表1 Δkp的模糊规则

表2 Δki的模糊规则表

表3 Δkd的模糊规则表

根据上述模糊规则表，可以对kp，ki，kd进行动态整定。通过状态方程(3)和期望的闭环传递函数(5)，求得k'p，k'i，k'd的预整定值分别为: k'p=19 638.65，k'I=603 880.52，k'D=215.68。选择适当的模糊化和去模糊化方法，得到模糊PID参数分别为:kp=k'p+Δkp，ki=k'i+Δki，kd= k'd+Δkd。

3 Matlab仿真分析

采用计算机仿真软件Matlab中的Fuzzy工具箱和M函数进行仿真［15］，验证模糊自整定PID控制器的性能。设定采样时间为1 ms，取1 000个采样点。单电磁铁悬浮控制系统的参数如表4所示:

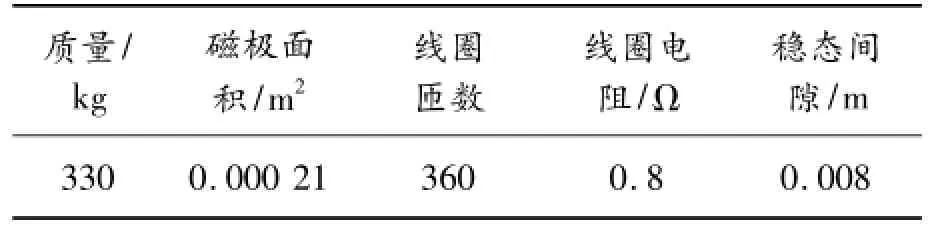
表4 单电磁铁悬浮系统的参数

针对轨道干扰和负载干扰问题，对比传统PID控制和模糊PID控制的跟踪效果。

3.1 轨道正弦波扰动的跟踪性能

设轨道不平顺对应的正弦波信号的幅值为1 mm，振动频率为2 Hz。仿真对比结果如图8所示。

图8 对轨道正弦波扰动的跟踪性能比较

3.2 轨道方波扰动的跟踪性能

设轨道不平顺所对应的方波信号的幅值为0.001 mm，振动频率为2 Hz。仿真对比结果如图9所示。

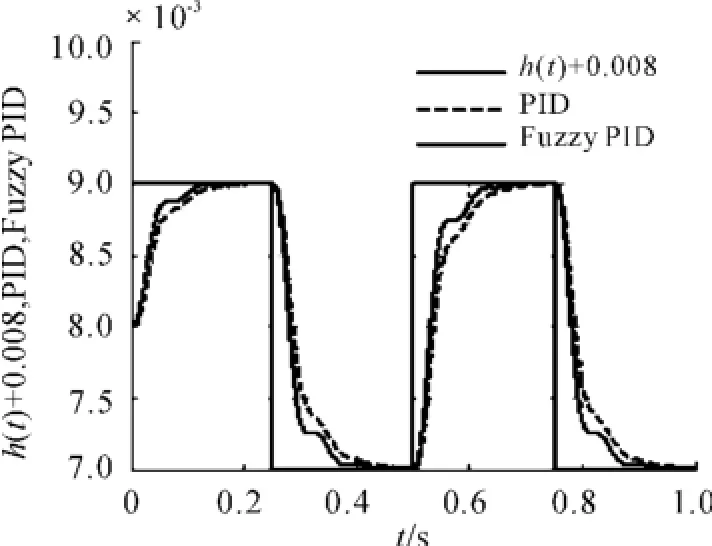
图9 对轨道方波扰动的跟踪性能比较

3.3 带有干扰信号轨道阶跃扰动的跟踪性能

设轨道所对应的阶跃信号为h(t)=0。在第300个采样点处，加干扰ξ(300)=0.005，仿真对比结果如图10所示。

图10 抗负载扰动的性能

4 结束语

本文首先建立3阶悬浮系统，增加干扰项，然后以电流为控制量，基于模糊免疫PID控制器设计控制方案，利用PSO寻优算法求解控制参数，最后，基于Matlab中的M函数形式进行轨道不平顺的跟踪研究。研究结果表明:

1)由于轨道不平顺对悬浮系统的影响，因此悬浮系统的控制性能对PID控制参数有很强的依赖性。要克服轨道干扰，就必须在线调整控制参数以获得最佳的系统控制特性。模糊自整定PID控制可以根据模糊控制规则实现在线调整PID参数的功能。

2)对于轨道的正弦波扰动及方波扰动，与传统的PID相比，模糊自整定PID控制均表现出较好的跟踪性能;对于负载扰动，该系统有较好的抑制性能。上述结果表明:与传统的PID控制相比，模糊自整定PID控制能够更好地解决轨道不平顺问题。

一个理论必须在实践中得到成功的应用才能推动其不断完善和向前发展，模糊控制理论亦如此。今后的研究将考虑如何将其和智能控制的方法相结合，以更好地应用于磁悬浮控制。

［1］Zhiqing Long，Guohua Shi，Lianchun Wang.Suspension influence analysis of track irregularity of maglev train［C］//Control and Decision Conference.［S.L.］:［s.n.］，2010:942－947.

［2］Hengkun Liu，Xiao Zhang，Wensen Chang.PID control to Maglev train system［C］//Industrial and Information Systems，［S.l.］:［s.n.］，2009:341－343.

［3］Moazen M，Sharifian M B B，Afshari H.PID control of Maglev guiding system for linear elevator［C］//Power E－lectronics，［S.l.］:［s.n.］，2012:1－6.

［4］汪培庄，李洪兴.模糊系统理论与模糊计算机［M］.北京:科学出版社，1996.

［5］Shing－Jen Wu，Cheng－Tao Wu，Yen－Chen Chang.Neural－Fuzzy gap control for a Current/Voltage－controlled 1/4－vehicle maglev system［J］.Intelligent Transportation Systems，2008(9):122－136.

［6］Ahmad A K，Saad Z，Osman M K，et al.Control of magnetic levitation system using fuzzy logic control［C］// Computational Intelligence，Modelling and Simulation (CIMSIM)，2010 Second International Conference on Digital Object Identifier.［S.l.］:［s.n.］，2010:51－56.

［7］Yang Xia，Gao Yan，Du Jiguang.P－Fuzzy－PID control in a machine tool magnetic suspension system［C］//Electrical Machines and Systems，2008 ICEMS.USA:［s.n.］，2008:2201－2204.

［8］Jie Ma，Wenjun Fan，Fenghua He.Parameters self－adjusting fuzzy PID control in magnetic levitation system［C］//Systems and Control in Aerospace and Astronautics，2008 ISSCAA.USA:［s.n.］，2008:1－5.

［9］Trisanto A，Yasser M，Jianming Lu，et al.Implementation of a Fuzzy PID controller using neural network on the magnetic levitation system［C］//Intelligent Signal Processing and Communications.USA:［s.n.］，2006:669－672.

［10］Qing Hu，Hao Liu，Lisheng Ou.Fuzzy PID nonlinear control of maglev guiding system for linear elevator based in feedback linearization［C］//Fuzzy Systems and Knowledge Discovery(FSKD)，2010 Seventh International Conference.USA:［s.n.］，2010:1277－1280.

［11］宋荣荣.单电磁铁悬浮系统的指数趋近律滑模控制［J］.重庆理工大学学报:自然科学版，2012，26(1): 11－16.

［12］李惠光，张广路，周巧玲，等.垂直轴磁悬浮风电悬浮系统的模糊滑模控制［J］.武汉理工大学学报，2010，32(10):136－140.

［13］郑大钟.线性系统理论［M］.北京:清华大学出版社，2002.

［14］陶永华.新型PID控制及其应用［M］.北京:机械工业出版社，1998.

［15］张智星.Matlab程序设计与应用［M］.北京:清华大学出版社，2002.

(责任编辑 刘舸)

Application of Fuzzy PID Controller in the Magnetic Levitation System

SONG Rong－rong1，MA Wei－hua2
(1.College of Computer Science and Technology，Southwest University for Nationality，Chengdu 610041，China;2.Traction power state key laboratory Southwest Jiaotong University，Chengdu 610031，China)

Based on the theory of fuzzy control，the article established the mathematical model of the electromagnetic levitation system，found out the fuzzy relation between the three parameters of PID and the two input variables of error and error change rate and instituted the more appropriate fuzzy control rules according to the characteristics of single electromagnet levitation system combined with the expert experience.Then we designs a fuzzy self－tuning PID controller.The advantages of the control strategy is that it is able to adjust PID parameters online in the suspension system work adapting to the change of the track irregularity，which makes the controller to be high tracking accuracy，fast response，andgood robustness.Using the organic combination of Fuzzy and Simulink in Matlab，the fuzzy self－tuning PID control system is feasible through the simulation，the results shows that the fuzzy self－tuning PID control can be more effective to track rail low frequency changes，has stronger suppression ability for the high frequency vibration caused by the track irregularity compared with the traditional PID controller.The article provides a very good method for solving problem of track irregularity.

track irregularity;magnetic levitation system;fuzzy PID control;Matlab simulation

TP13

A

1674－8425(2014)05－0001－06

10.3969/j.issn.1674－8425(z).2014.05.001

2013－12－18

国家自然科学基金资助项目(51005190)，四川省科技支撑计划项目(2012GZ0103)，西南民族大学中央高校专项资金项目(12NYZQN19)

宋荣荣(1979—)，女，博士研究生，副教授，主要从事泛函分析方面的研究。

宋荣荣，马卫华.模糊PID控制在磁悬浮系统中的应用［J］.重庆理工大学学报:自然科学版，2014(5):1－6.

format:SONG Rong－rong，MA Wei－hua.Application of Fuzzy PID Controller in the Magnetic Levitation System［J］.Journal of Chongqing University of Technology:Natural Science，2014(5):1－6.