大定源瞬变电磁均匀层状介质正演计算

柳建新，张 维*，曹创华，蔡 盛

(1．中南大学 地球科学与信息物理学院，长沙 410083；2．有色资源与地质灾害探查湖南省重点实验室，长沙 410083；3．中南大学 地质调查研究院，长沙 410083)

0 引言

瞬变电磁法的主要工作装置有中心回线、重叠回线、大定源回线等，其中又以大定源回线装置应用最为广泛[1-2]。大回线源装置的工作方法是采用较长的发送回线,利用阶跃波电流场源激励,在大地产生过渡过程场,断电瞬间在大地中形成涡旋交变电磁场。在回线内外一定的范围内,可观测到这种由地下介质产生的二次感应电磁场,随时间变化的衰减特性,进而从测量得到的异常信号中分析出地下不均匀体的导电性能和位置,以达到解决地质问题的目的。大回线装置与目标体具有最佳耦合、异常幅值大、形态简单、受旁侧地质体影响小的特点,并对高阻层有很强的穿透能力,对低阻层有较高的分辨能力。这种装置对铺设回线的要求不是很严格,一旦铺好回线后,不仅可采用多台接收机同时工作,而且可以把接收线圈排成阵列,发展成阵列式接收的观测系统。这种场源具有发射磁矩大、场均匀及随距离衰减慢等特点,适合于密集点距采样,精细探测。

大回线由于面积较大，不能看作磁偶极子。因此，研究大回线源激发的电磁场有着重要的意义。国内、外对大回线源产生电磁场的研究并不多，翁爱华[3]等首先求出任意一层电磁波的反射系数和透射系数，然后据此计算了圆形发射回生的频率域电磁场；M. Poddar[4]根据电磁学互易原理和垂直磁偶源产生的电磁场；求解出距形发射回线产生的频率域电磁场；Nagendra Partap Singh等[5]利用超几何分布函数，化简了圆形发射回线电磁场表达式中贝塞尔函数的乘积，从而求解出频率域电磁场。

作者从基本的电磁场理论出发，给出大回线发射源框内外不同位置的电磁响应表达式，利用一种新的算法计算电磁响应，并与传统的线性数值滤波法计算结果进行了对比分析(对比所用的滤波权系数，采用Anderson 计算的801个系数)。

1 理论基础

ε算法是一种递归方法，主要是基于以下三组关系式[7-8]：

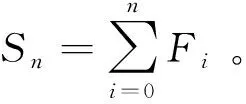
每个区间上的积分，采用以下形式计算：

式中m是积分阶数；w是与横坐标x有关的权重向量。

通过对上述方程做简单的变换，可以变换成与FHT算法一样的形式：

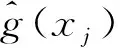
2 回线源瞬变电磁响应理论分析

图1为大回线源瞬变电磁法工作装置图。置于地表的发送线框激发的阶跃波，会在地下形成涡流场，回线电流的通断过程中，在回线内的磁通量会发生变化，通过分析接收线框接收到的磁通量变化信息，可以获知地下介质的分布情况。

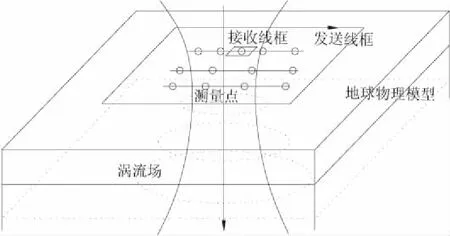
图1 大定源回线瞬变电磁工作布置示意图Fig．1 Working schematic of transient electromagnetic method in large loop source

在层状介质情况下，由阶跃电流激发，在发送线框内任意位置接收的频率域电磁响应为[9]：

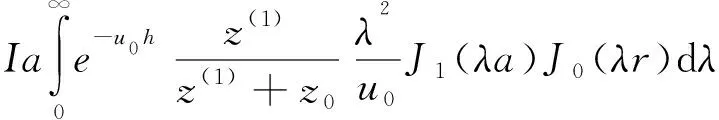
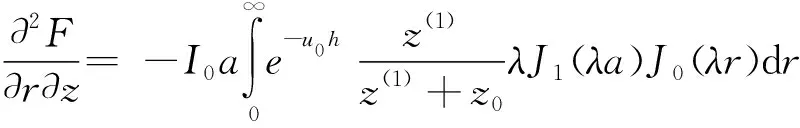
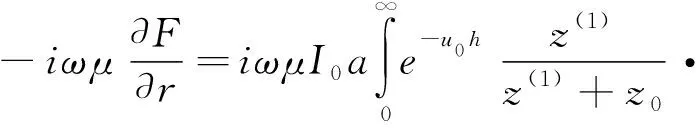
其中Hr(ω)、Eφ(ω)为径向的磁场分量和电场分量；Hz(ω)为垂向磁场分量；a是回线等效半径；I是发送电流；z0是表层阻抗；z(1)是总的波阻抗；h为发送线框距地面高度；r为发送线圈中心点与接收线框中心点之间的距离。波阻抗由以下公式计算[10]得到：

Hn为层状介质第n层的厚度。

z(n)=znzj=-iωμ0/uj

z0=-iωμ0/u0=-iωμ0/λ

3 计算结果分析

计算都是基于均匀层状介质模型进行的。ρ1=100 Ω·m，ρ2=1 000 Ω·m，a=100 m，H=40 m，发送电流为I=1 A，发送频率为f= 25 Hz。

图2和图3描述了积分核函数的收敛情况。由图2可知，对于h= 0 m的情况，零阶和一阶的第一类贝塞尔函数在λ增大的时候，振荡很明显，这是贝塞尔函数本身的性质。除去贝塞尔函数之后，核函数剩余部分的虚部是单调递减的，而实部则是单调递增的。在h= 5 m 时(图3)，除去贝塞尔函数之后的核函数虚部仍然是单调递减的，而实部则是随λ增大而增大，达到一个最大值后开始随λ增大而减小。

由Anderson 的研究可知，在利用快速汉克尔变换计算贝塞尔函数积分的时候，积分核函数(除去贝塞尔函数)必须是单调递减的。所以对于h= 0 m的情况，用汉克尔变换不能得到稳定的解(图4)。

对于垂向磁场实部的计算：在h= 0 m时(图4)，利用FHT算法得到的结果跳动比较厉害，而且在r>a时，计算结果误差较大，而用QWE法得到的结果除了在r= 100 m附近出现一个极大值外，在框内、外的计算结果都比较稳定；在h= 5 m时(图5)，两种方法的计算结果曲线趋势是一样的，不过用QWE算法得到的计算结果相对较稳定。对于虚部的计算，两者的计算结果吻合的都非常好。通过上面的分析可知，这是因为核函数的虚部是收敛，所以利用FHT算法计算能得出比较精确的结果。

此外，由于QWE计算积分时的求积点是不均匀分布的一些高斯积分点，计算的核函数的数量是随r的变化而变化的，而数值滤波法由于滤波权系数数量是固定的(801个)，所以计算的核函数的数量是不随r变化的。由图6可以看出，对于大多数的r，用QWE算法所需计算的核函数数量都是少于用FHT算法的。

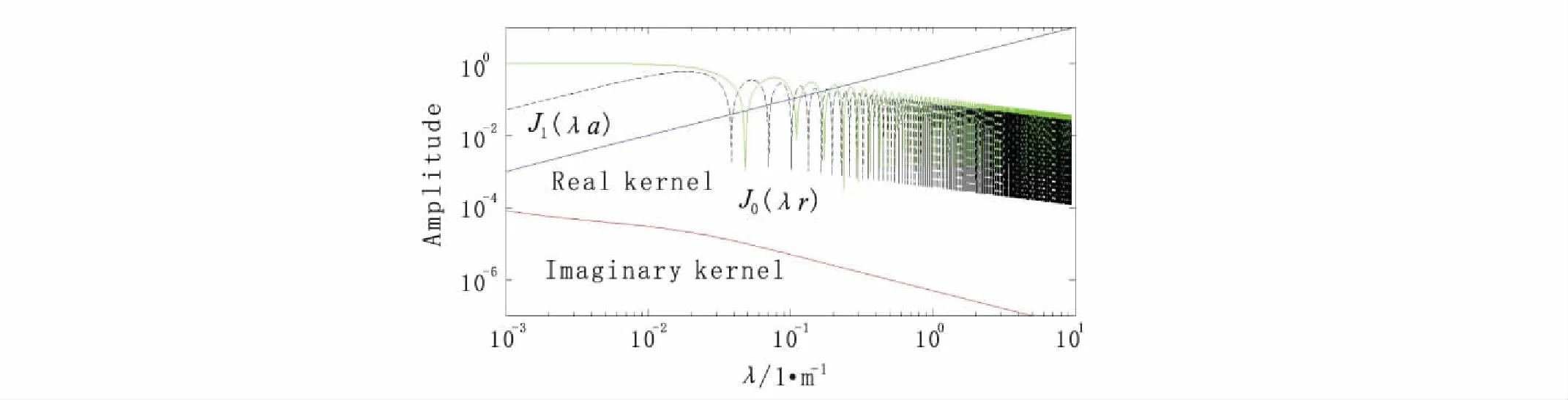
图2 r =50 m，h =0 m 时，积分核函数(不含贝塞尔函数)及贝塞尔函数性质Fig．2 Characteristics of kernel functions (without the Bessel functions) and Bessel functions when r =50m, h=0 m

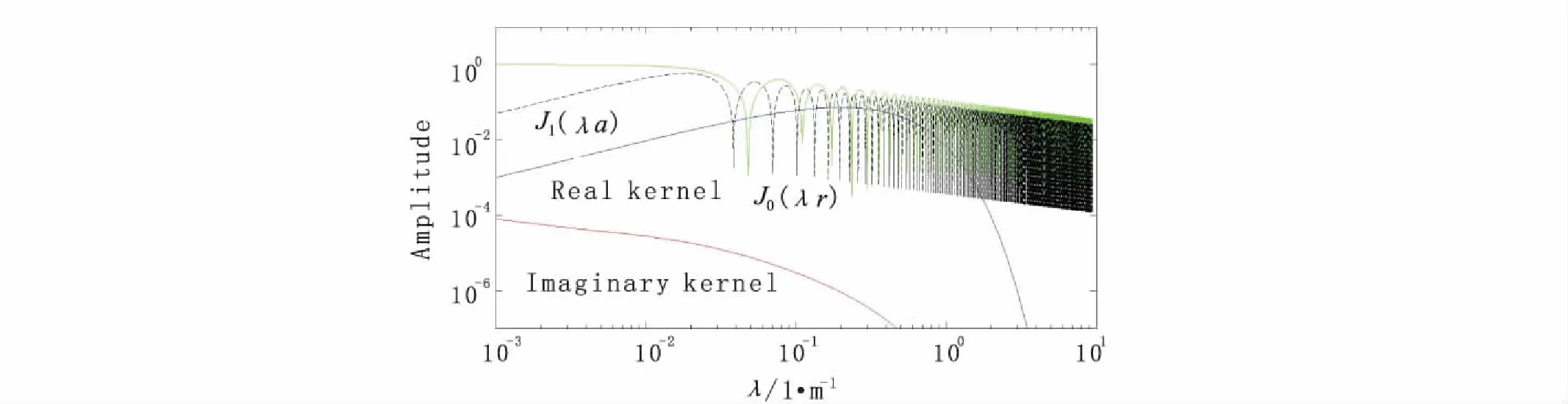
图3 r =50 m，h =5 m 时，积分核函数(不含贝塞尔函数)及贝塞尔函数性质Fig．3 Characteristics of kernel functions (without the Bessel functions) and Bessel functions when r =50 m, h =5 m

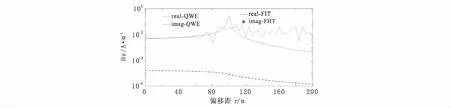
图4 h=0 m时，两种方法在不同偏移距条件下实部和虚部响应对比图Fig．4 Comparison of real and imaginary responses by each method in different offset, h=0 m

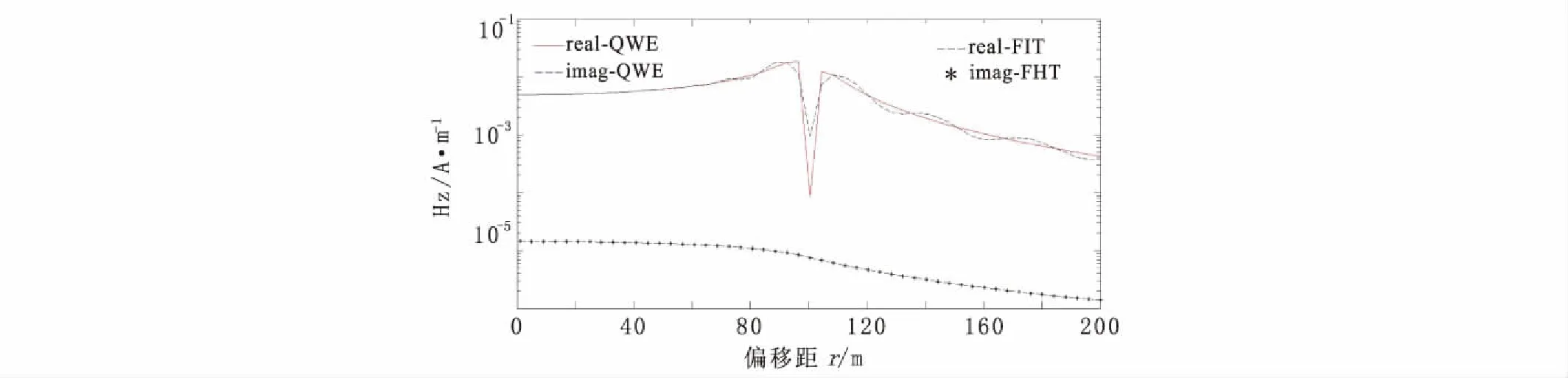
图5 h = 5 m时，两种方法在不同偏移距条件下实部和虚部响应对比图Fig．5 Comparison of real and imaginary responses by each method in different offset, h=5 m

4 结论

作者对大回线源瞬变电磁法一维层状正演算法进行了研究，将QWE方法与传统的基于快速汉克尔变换的数字滤波法进行了比较：两者对于虚部的计算吻合比较好；然而对于实部的计算，QWE算法计算的结果相对较稳定，尤其是对于线框位于地表的情况，FHT算法对于不同偏移距的计算结果变化较大，而QWE算法的结果比较稳定；此外QWE算法所需计算的核函数数量随偏移距的不同是不断变化的，在大多数偏移距条件下，所需计算的核函数数量均少于数字滤波法。

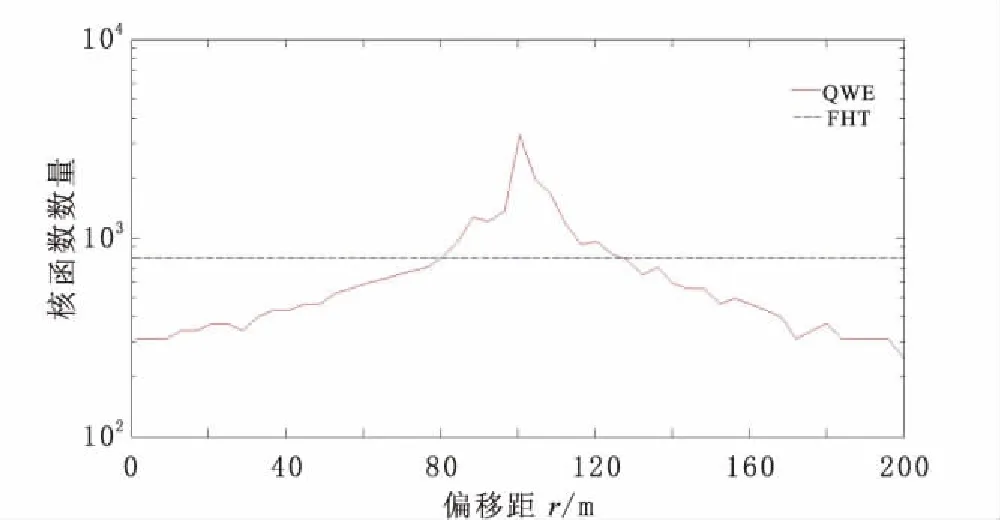
图6 h =0 m时，两种方法不同偏移距条件下核函数计算数量对比Fig．6 Comparison of the number of kernels evaluations required by each method in different offset

参考文献：

[1] 薛国强, 秦克章, 黄树峰,等.大回线源瞬变电磁技术在西藏山南地区探矿中的应用[J].地质与勘探,2011, 47(1):100-106.

[2] 徐贵东, 黄继军, 刘德军,等.瞬变电磁在吉林省红旗岭铜镍矿勘查中的应用[J].吉林地质, 2010, 29(4): 79-82.

[3] 翁爱华,李舟波,王雪秋.地表大回线源在任意层状介质中产生磁场的计算[J].物探化探计算技术, 2000, 22(3):245-248.

[4] PODDARM A. Rectangular Loop Source of Current on a Two-layered Earth[J]. Geophys,Prosp, 1982, 30:101-114.

[5] NAGENDRA PARTAP SINGH, TORU MOGI. Electromagnetic Response of a Large Circular Loop Source on a Layered Earth: A New Computation Method[J]. Pure and Applied Geophysics,2005, 162:181.

[6] LONGMAN I M. Note on a method for computing infinite integrals of oscillatory functions: Mathematical Proceedings of the Cambridge Philosophical Society[J].Mathematical proceedings of the Cambrige Philosophical Society,1956,52(4): 764-768.

[7] SHANKS D. Nonlinear transformations of divergent and slowly convergent sequences[D]．Journal of Mathematical Physics, 1955, 34：1-42.

[8] KERRY KEY.Is the fast Hankel transform fast than quadrature[J]．Geophysics, 2012,77(3): 21-30.

[9] 考夫曼A.A, 凯勒.G.V.频率域和时间域电磁测深[M].北京:地质出版社,1987.

[10] 牛之琏.时间域电磁法原理[M].长沙：中南大学出版社, 2007.

[11] ANDERSON W L. Fast Hankel-transfroms using related and lagged convolution[J]．ACM Transforms on Mathematical Software, 1982, 8(4)：344-368.

[12] GUPTASARMA D B. Singh. New digital linear filters for Hankel J(0)and J(1)transforms[J]. Geophysical Prospecting, 1997, 45:745-762.

[13] 方文藻,李予国,李貅.瞬变电磁测深法原理[M].西安:西北工业大学出版社,1993.

[14] 李貅.瞬变电磁测深的理论与应用[M].西安：陕西科学技术出版社, 2002.

[15] 薛国强,李貅,郭文波.大回线源瞬变电磁响应[J].石油地球物理勘探,2007,42(5):586-590.

[16] CHAVE A D. Numerical integration of related Hankel transforms by quadrature and continued fraction expansion[J].Geophysics, 1983, 48:1671-1686.

[17] 刘继东, 方文藻. 用线性数字滤波法计算大回线源在地下形成的瞬变电磁场[J].物探化探计算技术, 1996, 18(4):231-237.

[18] 李建慧, 刘树才, 李富,等.大定源瞬变电磁法矩形发射回线激发的电磁场[J]．物探化探计算技术, 2008, 30(2):154-157.