基于传输线法模拟探地雷达在多层介质模型中的传播

李 婷，刘 策，2，郭 晨，张 勇

(1.信息工程学院 长安大学， 西安 710064；2.浅层探测与测井研究实验室 休斯敦大学，德克萨斯州 美国 77004)

0 引言

探地雷达是一种近几十年发展起来的一种地下目标的有效探测手段，通过分析检测到的雷达数据，可以获得测量物质的有效信息。正演数值模拟可以有效地模拟电磁波在地下结构中传播，是解释探地雷达数据的重要方法。探地雷达数值模拟方法主要包括时域有限差分法(Finite difference time domain method)[1]、有限单元法(Finite Element Method)[2]、射线追踪法[3]、积分方程法[4]等，其中FDTD是应用最广泛的方法，适合物理参数分布简单或几何特征规则的模型。事实上，与FDTD方法相对应的另一种时域方法即传输线矩阵法[5-7]，同样具备FDTD方法的优点。

传输线法是由Johns和Beurle[7]提出的一种时间域分析电磁场方法。TLM方法基于Huygens波的传播原理，通过研究时间和空间上的离散波在不同导波结构中的传播情况，来获得导波结构的种种传输特性。该方法最初应用于波导的不连续性及散射问题的分析，随着计算机技术的发展，近年来TLM被广泛应用在微波、数字电路仿真、电磁散射、雷达探测模拟、石油测井等具有波传播特征的领域中。作者应用TLM方法进行均匀多层介质的正演模拟，通过典型激励得到了合成的反射波，并与已有的FDTD算法进行比较，验证了TLM方法的正确性和适用性。

1 TLM原理

1.1 Maxwell方程组

TLM方法是依据传输线矩阵中的电压电流方程与Maxwell方程组的类比性，用传输线矩阵网格中的电压和电流脉冲来模拟某区域中的电磁场传播。如图1所示，电磁脉冲发射出的电磁波垂直穿透介质层表面，脉冲探头处的电池强度用I(t)表示，其中I(t)随着时间的变化而发生变化。对TM模而言，此时区域的电磁场关系，场分量为Ez、Hx、Hy, Maxwell方程可表示如下：

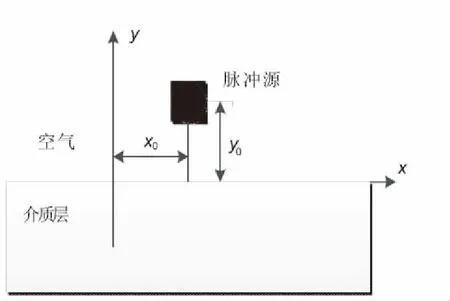
图1 位于(x0,y0)处的电磁脉冲源Fig．1 An electromagnetic-pulse source locate on the (x0,y0)

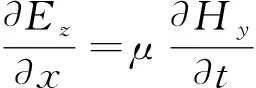
(1)

(2)

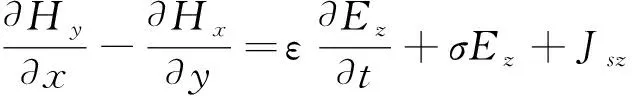
(3)

其中μ、σ和ε分别为磁导率、电导率和介电常数；Jsz为发射源的电流密度。

定义

Jsz=I(t)δ(x-x0)δ(y-y0)

(4)

其中δ为单位脉冲函数。

1.2 传输线网络方程与Maxwell方程间的关系

在TLM方法中，均匀的二维空间可以用传输线来模拟。我们可以将图1中的介质层划分成网格为M×N的传输线网络(图2)。它实际上是一个半波系统，每隔Δl的距离都联接着一对长为Δl/2的开路线(图3)。则传输线方程可表示如下：

(5)

(6)

(7)

其中Lx和Ly分别为x、y轴上电感；C为电容；G为电阻器；Is是单位为安培电流源。

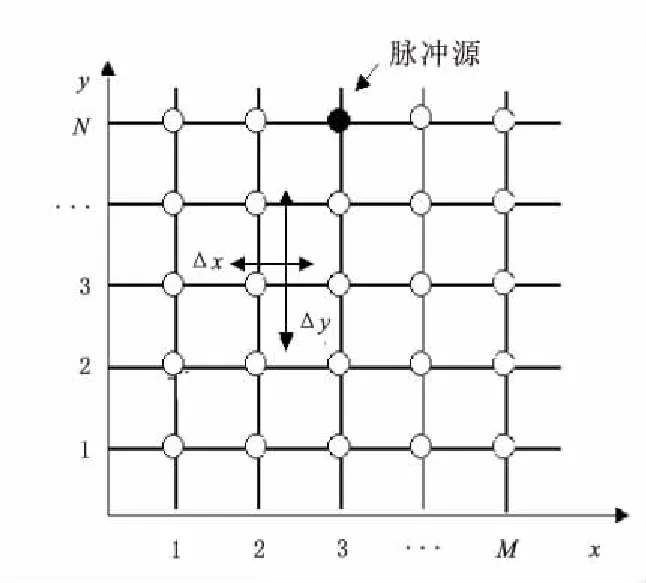
图2 网格为M×N的传输线网络Fig．2 M×N-transmission line network

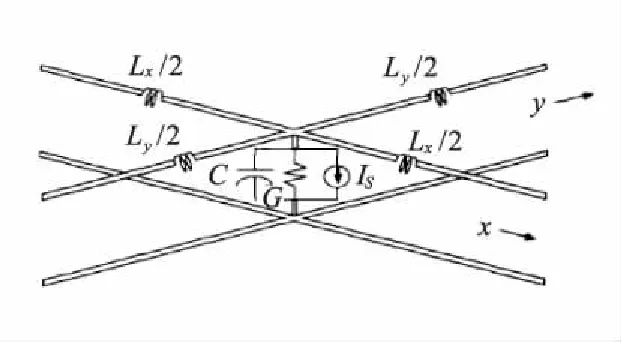
图3 网格单元等效电路图Fig．3 Equivalent circuit of the TLM cell

通过对比式(1)-式(3)与式(5)-式(7)发现，传输线网络方程与二维电磁场波动方程的关系如下：

V=EzΔz

(8)

Ix=-ΔyHy

(9)

Iy=ΔxHx

(10)

(11)

(12)

(13)

(14)

Is=I(t)

(15)

1.3 传输线中的节点表达式

为了计算传输线中每个节点的电压与电流，我们在这里定义节点的阻抗为C，由图3可知，此节点的阻抗可以定义为：

C=Cx+Cy+Cs

(16)

其中Cx、Cy分别为x、y轴上的电容值；Cs为并联电容的电容值。

在传输线矩阵中，电压或电流沿传输线矩阵传播，其传播速度v与传输线上的电容与电感有关，则x轴上的传播速度可以定义为：

(17)

传输线x轴方向上节点间的传播时间可表示为：

(18)

同理，y轴上节点间的传播时间可表示为：

(19)

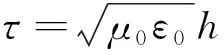
(20)

其中ε0、μ0分别为真空中的介电常数和磁导率；h为传输线长度，由文献[8]中可知h需满足以下条件：

(21)

由公式(11)、式(12)、式(19)、式(20)可以推导出Cx、Cy的表达式：

(22)

(23)

最终Cs可以由公式(13)、式(16)、式(22)、式(23)得到，即

(24)

同理可得到传输线上的导纳特性，即

(25)

(26)

(27)

图3中的并联电容可以由半无限均匀无损耗传输线表示，即可得到

Y∞=G

(28)

1.4 传输线网络中的节点关系

在均匀介质中，波的传播过程[9]如图4所示，等效为电压波在传输线网格上传播。图4(a)中为传播过程的初始状态，设想输入一个幅度为1V的冲激脉冲，它们在末端形成的电压反射系数为(1/2，结果就形成了图4(b)的结果，依次类推，图4(c)为迭代两次的结果，图4表明了电压波在传输线矩阵上的传播过程。

我们将电压波在传输线图络上的传播具体化，以便形象地解释节点电压间的关系。图5中各节点电路形式与图3等效相同，分支(1)、分支(3)分别为X轴上的线电阻，分支(2)、分支(4)分别为y轴上的线电阻，分支(5)为开路节点，分支(6)等效为半无限均匀无损耗传输线。

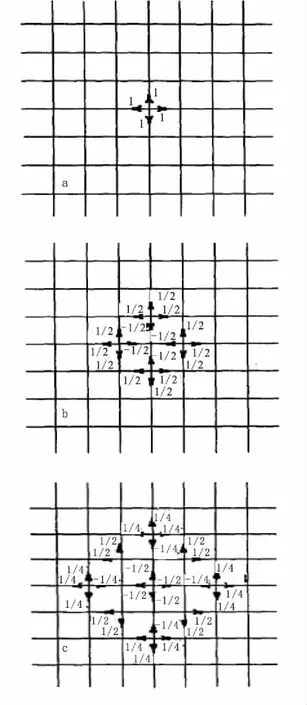
图4 电压波在传输线网络上的扩散过程Fig．4 The voltage wave diffusion on the transmission line network (a)初始状态；(b)第一次迭代；(c)第二次迭代

设V(m,n,p)为t=p(时的网格(m,n)处的节点电压，Vr(m,n,k,p) 、Vi(m,n,k,p)为第k个分支上的反射电压和传输电压，节点分支如图5所示。

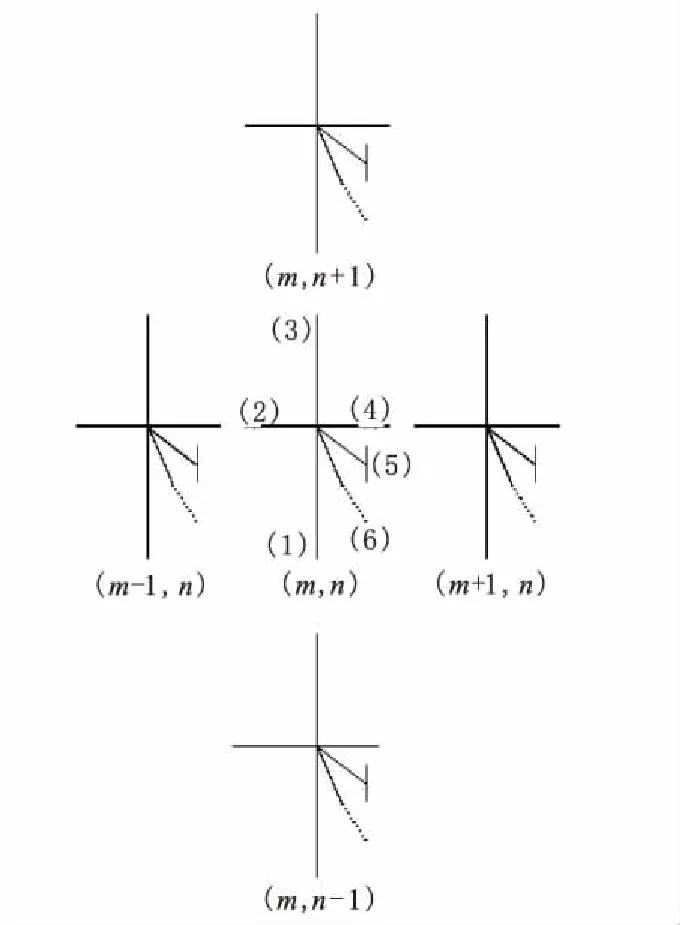
图5 单元节点(m,n)与其相邻节点Fig．5 Node(m,n ) and its adjacent node

在二维介质中，任意单元节点(m,n)都与四条TLM线相邻，每条TLM线上存在正向波和反向波，而每条线上的正向波和反向波又分别来自四条TLM线上波的贡献。则每个节点的电压都可由式(29)表示。

(29)

其中Vr(m,n,k,p)和Vi(m,n,k,p)分别定义为5X1的矩阵，其中k=1,2,…。

节点反射电压定义如下：

[Vr(m,n,k,p)]=[S][Vi(m,n,k,p)]

(30)

式中S为5×5的矩阵，其表示为：

(31)

而矩阵中的 Γ和T可定义成如下形式：

(32)

(33)

(34)

Tx=1+Γx

(35)

Ty=1+Γy

(36)

Tc=1+Γc

(37)

矩阵元素S11=Γy表示分支1上的反射系数，S21=Ty代表分支2与分支1之间的传输系数。以此类推，矩阵中对角线上的元素分别代表不同分支上的反射系数，其余元素则为不同分支间的反射系数。

每个节点的传输电压由两部分组成，一部分是来自该节点的反射电压，另一部分为相邻4个节点上的传输电压。 每一个分支的传输电压可表示如下：

Vi(m,n,1,p)=U1Vr(m,n,1,p-1)+

W1Vr(m,n-1,3,p-1)

(38)

Vi(m,n,2,p)=U2Vr(m,n,2,p-1)+

W2Vr(m-1,n,4,p-1)

(39)

Vi(m,n,3,p)=U3Vr(m,n,3,p-1)+

W3Vr(m,n+1,1,p-1)

(40)

Vi(m,n,4,p)=U4Vr(m,n,4,p-1)+

W4Vr(m+1,n,2,p-1)

(41)

反射系数U和传输系数W可表示如下：

(42)

(43)

(44)

(45)

Wk=1-Uk,k=1,…,4

(46)

由公式(38) - 公式(41) 中可知，t=pτ时的传输电压Vi可由t=(p-1)τ时刻各点的反射电压获得。由公式(30)可以得到t=pτ时的反射电压Vr。依此类推，我们可以迭代计算出不同时刻各个节点的电压状态。

2 算法实现

由第二节TLM的原理及其计算迭代公式可知，只要知道任意t=(p-1)τ时刻，各节点上的电压大小与方向，就可以得到t=pτ时刻网络中各个节点上的场值。关于TLM的具体实现过程如图6所示，我们将TLM的基本算法步骤总结如下：

(1)设置模型。

(2)初始化节点反射电压，其中Vr(m,n,k,0)=0 表示在任意网格t=0时的反射电压为0，t=0时脉冲源处的电压为Vr(m0,n0,k,0)=Vs

(3)计算时间迭代，根据各个节点的入射电压及反射电压计算出节点总电压。

(4)迭代结束，输出计算结果。

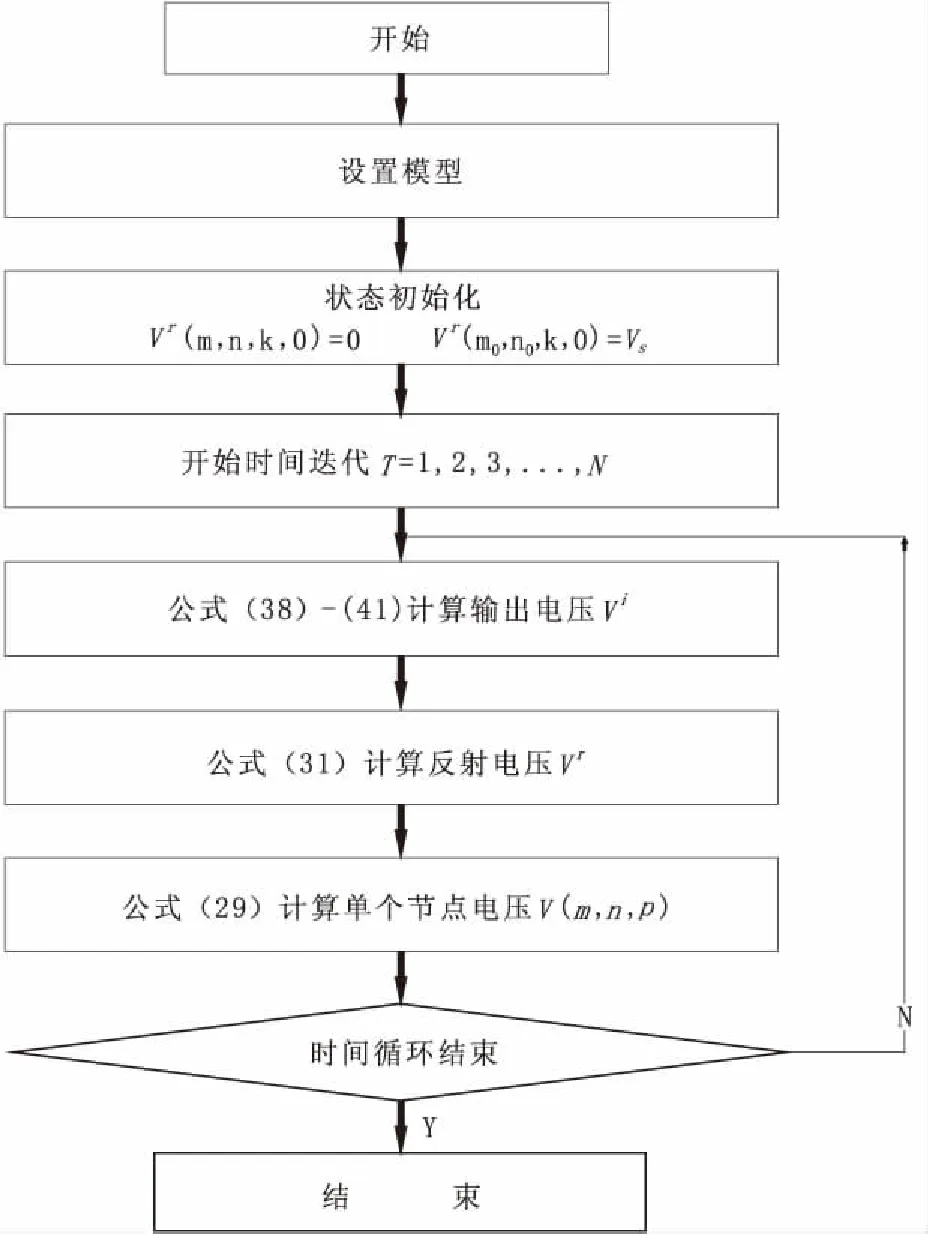
图6 TLM算法流程图Fig．6 Flow chart of TLM

3 数值算例

首先通过电磁波在多层介质中的传播问题来验证TLM算法的正确性。如图7所示， 假设雷达发射端与接收端相距0.5 m，测试模型共有三层介质层，各层介电常数与电阻率分别为4、0.005；6、0.01；8、0.02。雷达发射脉冲采用中心频率为1 GHz的正弦脉冲，如图8所示。

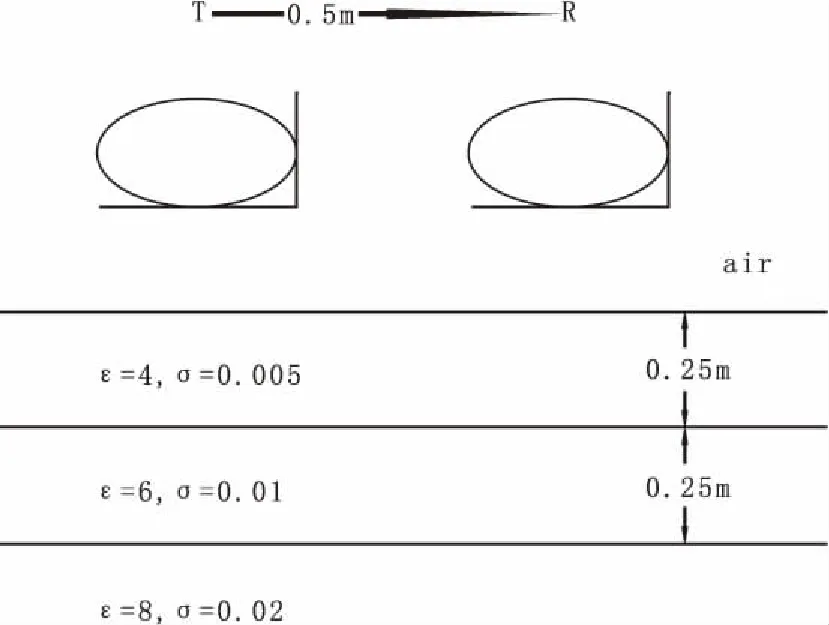
图7 测试模型Fig．7 Test model

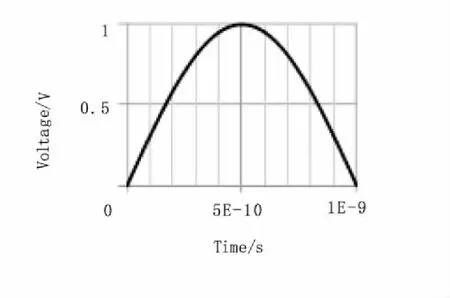
图8 雷达入射脉冲Fig．8 Radar pulse

通过对比图9中TLM方法与FDTD方法的正演模拟结果，可以发现，TLM算法与FDTD方法可以达到同样的正演效果。

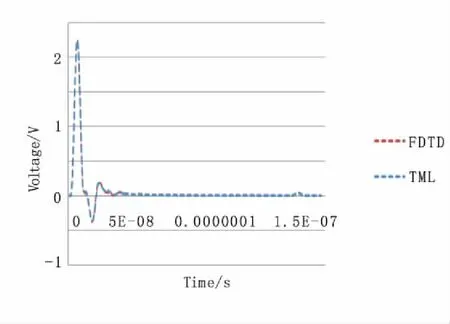
图9 TLM与FDTD正演模拟结果Fig．9 Forward modeling result of TLM and FDTD

改变图7模型中第一层介质的介电常数值，其余参数保持不变。分别将介电常数改为4、6、8、16。通过TLM方法模拟电磁波在介质层的传播，可以发现，在电导率不变的情况下，介质层介电常数的增加，将会导致电磁波间的衰减越来越大，而反射脉冲的强度越来越低。

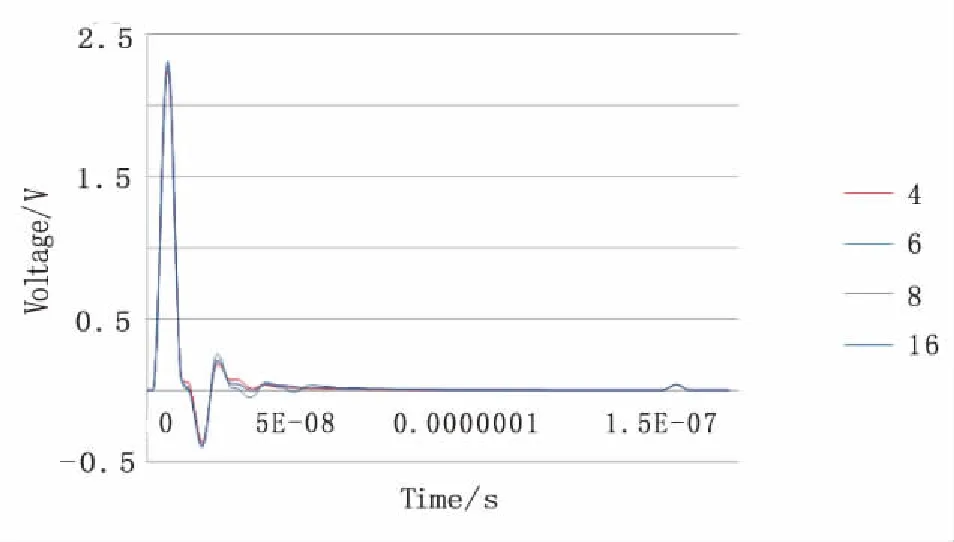
图10 第一层介质电导率不变，改变介电常数分别为4、6、8、16，得到的正演模拟结果图Fig．10 The forwarding modeling result: the conductivity of 1st-layer is the same as the test model, changed dielectric constant to 4,6,8 and 16,respectively

同样条件下，改变第一层介质的电阻率，通过仿真发现，在介电常数不变的情况下，电导率越大，物质对电磁波的吸收越大，电磁波衰减地越快。

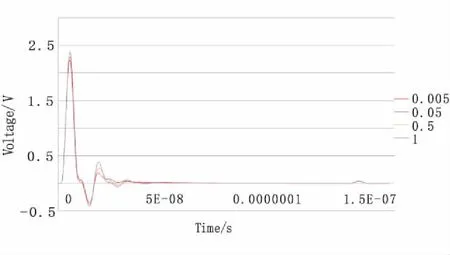
图11 第一层介质介电常数不变，改变电导率分别为0.005、0.05、0.5、1，得到的正演模拟结果图Fig．11 The forwarding modeling result: conductivity of the 1st layer is the same as the test model, changed conductivity to 0.005、0.05、0.5 and 1,respectively

4 结论

作者应用二维TML方法模拟探地雷达电磁波在均匀多层介质模型中的传播，通过对比本文算法与时域有限差分法模拟结果可以看出，两种算法计算结果吻合非常好，这表明了TLM算法用于雷达波模拟的正确性和有效性。同时将TLM算法用于对已有模型的定性分析，结果表明：介电常数和电导率对雷达电磁波有很大影响，随着介电常数和电导率的增大，雷达波的衰减越快，介质层对电磁波吸增加。

参考文献：

[1] TING LI, CE LIU, CHEN GUO ,et al. Research on absorbing boundary condition in FDTD method [C]// Computer Science and Network Technology 2012 2nd International Conference.Changchun,China, 2012: 1574-1577.

[2] 冯德山,陈承申,王洪华. 基于混合边界条件的有限单元法GPR正演模拟[J].地球物理学报, 2012,55(11): 3774-3785.

[3] 邓世坤,王惠濂.探地雷达图像的正演合成与偏移处理[J].地球物理学报,1993,3(4):528-536.

[4] SIMSEK E, LIU JIANGUO, LIU QINGHUO. A Spectral Integral Method (SIM) for Layered Media [J]. IEEE Transactions on antennas and propagation,2006,54(6): 3878- 3884.

[5] LIU CE, SHEN, LIANG C. Numerical Simulation of Subsurface Radar for Detecting Buried Pipes[J].IEEE Transactions on Geoscience and Remote Sensing, 1991,29(5):795- 798.

[6] HOEFER W J R.The transmission line matrix method theory and applications[J].IEEE Transactions on Microwave Theory and Techniques,1985,33(10):882-893.

[7] JOHNS P B,BEURLE R L. Numerical solution of 2-dimensional scattering problems using a transmission-line matrix[J]. Proceedings of the Institution of Electrical Engineers,1971,118(9): 1203-1208.

[8] LIU C, SHEN L.C. Response of Electromagnetic-Pulse Logging Sonde in Axially-Symmetrical Formation[J]. IEEE Transactions on Geoscience and Remote Sensing,1991,29:214-221.

[9] CHRISTOPOULOS C.The Transmission-Line Modeling Method TLM[M]. IEEE/OUP Series on Electromagnetic Wave Theory, 1995.