伪随机激电法的有限单元法数值模拟研究

杨晓弘，曾凡秋

(湖南省有色地质勘查研究院，长沙 410015)

0 前言

长期以来电法勘探，包括激电法和电磁法在发现铜、铅、锌等金属矿产方面发挥了巨大的作用。然而，区分矿与非矿多年来一直是困扰矿产地球物理工作者的难题。地球物理学家何继善院士经过多年的理论研究与生产实践，提出了伪随机激电法理论。伪随机激电法的场源是采用2n系列伪随机信号波形电流作为电法的激励场源，接收经过介质响应后的伪随机多频电场信号和磁场信号，经处理、分析后提取地质信息，而达到电法勘探的目的。该激励场源可以应用于CSAMT、MT、IP、SIP、CR等。伪随机信号具有易于大功率发送的优点，与方波相比，其带宽是可控的。在实践测量中可以通过控制信号带宽来控制测量效率，从而完全改变了人工场源频率域电法勘探效率低这一缺点[1]。

不论是哪种地球物理勘探方法，在资料的解释方面都存在问题的多解性，由于物理模拟比较昂贵和数字计算又不太适合物性复杂分布的地质情况，所以数值模拟成为大多数地球物理工作者有力的工具[2-3]。作者试图通过对伪随机激电法进行正演数值模拟，来研究伪随机激电法的一些特点和属性，在伪随机激电法数值模拟方面进行一些有益的尝试。

1 伪随机激电法基本原理

2n系列伪随机、多频信号电磁法理论是由中国工程院院士何继善所发明和命名，激发信号随着n的不同，在时间域上具有不同的波形。但它们的频谱有一个共同的特点，就是它们的频谱在频率为2kω0(k=0, 1, 2, …,n-2,n-1；ω0为基波频率)共n个频率上大小基本相等，在这些频率上的功率之和占了信号总平均功率的大部分，其余谐波含有的功率只占信号总平均功率的小部分，2n系列伪随机信号的名称也因此得来。

用p(2,n,t)表示伪随机n频波，在周期[0,T)内可以表示为：

(1)

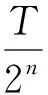
由于该方法场源包含多个频率，而且能同时接收和测量这些频率信号，所以该方法具有一次可以测量多个频率信号，减弱了由于干扰和电流变化等的影响，提高了测量精度，特别是相对精度，可以观测弱信号，发送电流小，仪器轻便，信息量丰富，可自动去除感应耦合等特点[1]。

2 数值模拟的基本原理与方法

2．1 数值模拟的基本原理

伪随机激电法也是频率域激电方法，对其进行数值模拟的出发点是Pelton定义的Cole-Cole模型[4-6]。Cole-Cole模型可以用式(2)来表示

(2)

其中ρ0为频率为零时岩、矿石的电阻率；m为充电率；c为频率相关系数；τ为时间常数。当激发电流的频率较低的时候可以忽略电磁效应的情况，这时可以用Cole-Cole模型得到的复电阻率或复电位来替换大地模型的地质体，通过求解大地模型得到不同频率下地表节点上的复电位值，就可以获得伪随机激电法数值模拟的参数[7-8]。

当激发电流频率较低的时候，可以在忽略电磁效应的情况下用稳定电流场的边值问题和变分问题对以上问题进行研究。三维构造中双点电源电场模型的电位边值问题为[9-10]

(3)

式中u为电位；σ为三维地下空间介质的电导率；I为电流强度；Ω为模型区域；n为边界的外法向方向；Γs为模型的地面边界；γA、γB为测点到电源点A、B的距离；Γ∞为无穷远边界。

与上述边值问题(3)等价的变分问题为

(4)

2．2 有限单元法

2.2.1 单元剖分

为方便程序的编制，用正六面体单元对大地模型进行剖分(图1，图2)。

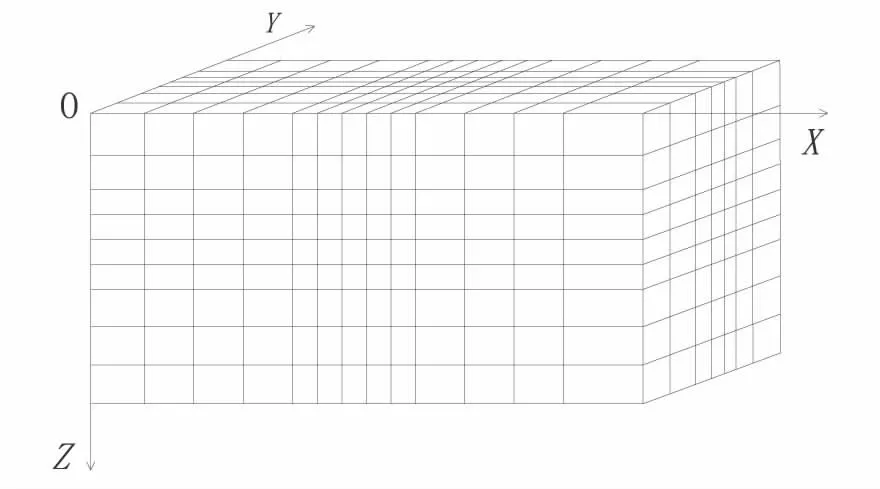
图1 模型剖分示意图Fig．1 Sketch of model division

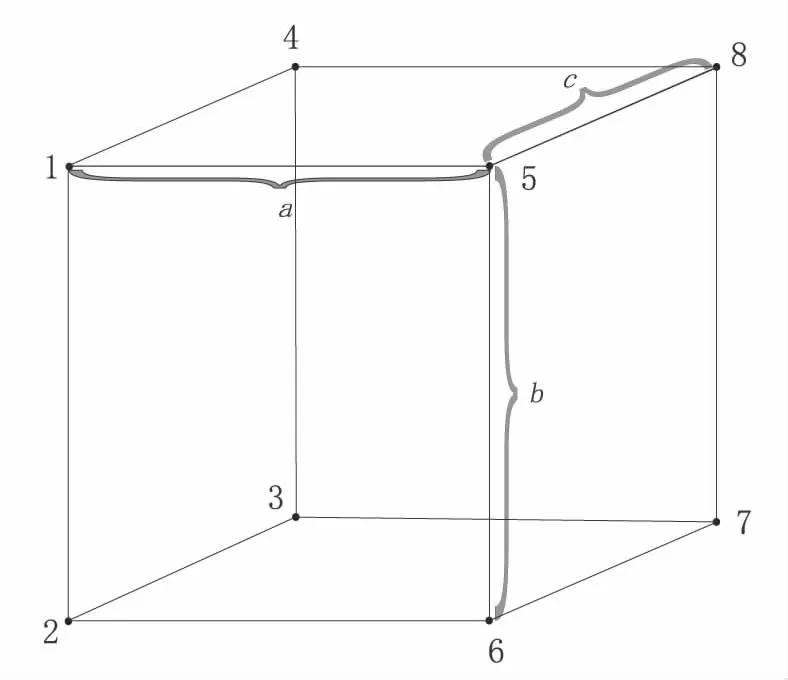
图2 剖分单元Fig．2 Element of the model

2.2.2 单元积分

经过线性插值后，对变分方程的单元积分变为

(5)

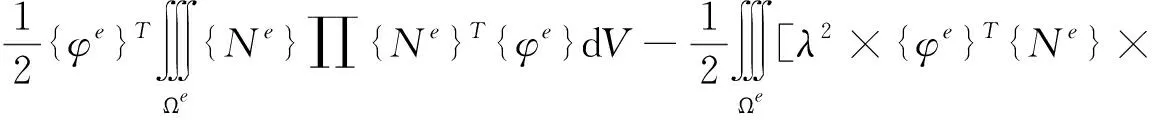
{Ne}T{φe}]dV

(6)

其中N为形函数。

式中ξi、ηi、ζi分别是等参单元中点i(i=1,…，8)的坐标。

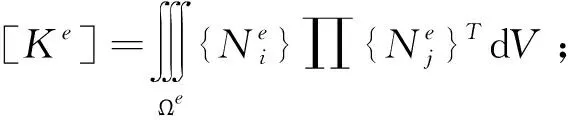
2.2.3 总体合成及求变分

(7)

令δF(φ)=0,

则有

[K′]{φ}-{b}{φ}=0,

即

{K}{φ}=0，其中K=[K′]-{b}。

2.2.4 解方程及计算视幅频率

解形如{K}{φ}=0的方程就得到模型中各个节点上的复电位值，伪随机激电法的基本参数都可以通过相应的定义计算得到。

3 模型计算

假设有一个大小为500 m×100 m×100 m三维均匀半空间大地模型，模型的剖面图如图3所示。

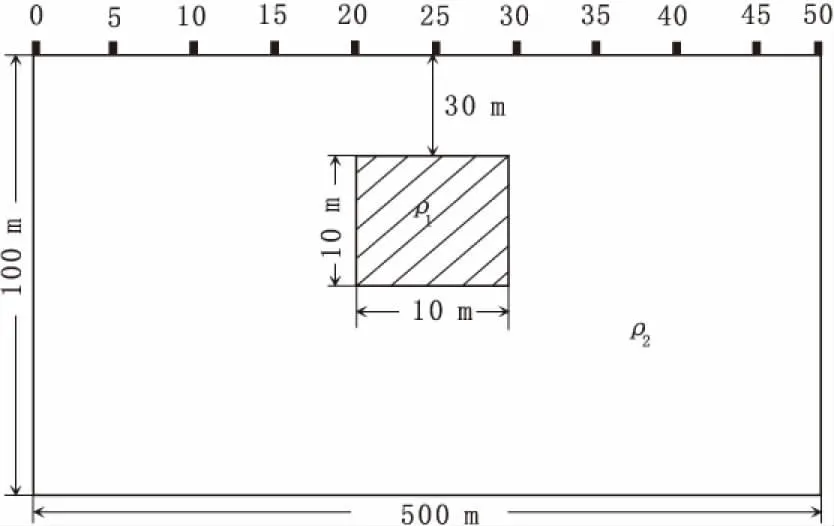
图3 模型断面示意图Fig．3 Sketch of the earth model

采用伪随机信号激发时，首先研究极化异常体的时间常数τ对幅频率的影响情况。当测量电极在极化异常体的上方地面中心位置固定的时候，选用的激励电流频率范为 0.000 1 Hz～10 000 Hz，极化异常体的m2=0.8、c2=0.25；大地介质中的m1=0.04、c1=0.25、τ1=1 s，采用不同的τ2值时就可得到对应的幅频率曲线图(图4)。

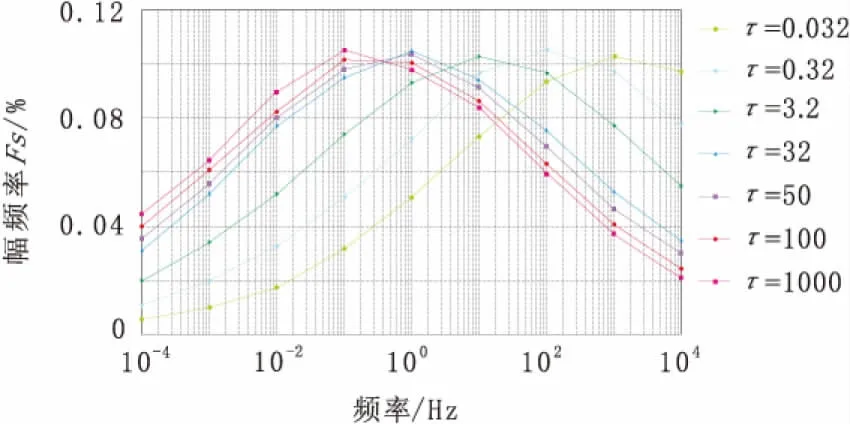
图4 不同时间常数对应的幅频率曲线(m=0.8,c=0.25)Fig．4 Curves of Fs in different time constant(m=0.8,c=0.25)

从图4可以看出，幅频率在某个频率上取得其极值，而随着频率的无限增大或无限减少，幅频率趋向于“0”值，即异常体来不及激化或激化已经趋于稳定。随着时间常数τ值的增大，幅频率极值频率向低频方向移动。幅频率的极值频率虽然随着时间常数的不同而不同，但幅频率的极值却相同，故时间常数不会影响幅频率的极值大小。时间常数也不影响幅频率曲线的形态，而只影响其位置。通过对比野外实测幅频率曲线，其极值频率能在一定程度上反映勘探区内的综合时间常数的大小，而大部分的金属硫化物的时间常数都很大，无激电效应或激电效应很小的围岩的时间常数一般较小，故通过比较幅频率的极值频率大小能对异常源作一定的定性解释。

图5是m对幅频率值的影响情况。当充电率从0.1变化到0.9时就能得到不同m2值所对应的幅频率Fs的曲线图。从该曲线图中可以看出，幅频率随着充电率m2的增大，其极值也变大，极值频率缓慢地向高频移动。这与实际情况相符，充电率与极化率、幅频率在发现异常上是等效的，且其值也是正相关。充电率的大小影响幅频率曲线的形态，而对于其位置影响很小。

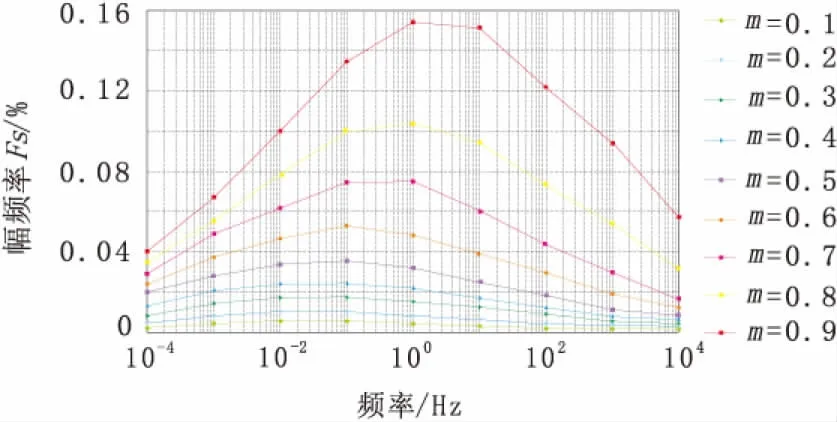
图5 不同充电率m对应的幅频率曲线(τ=50 s,c=0.25)Fig．5 Curves of Fs in different charge rate m(τ=50 s,c=0.25)

图6是不同的频率相关系数c2所对应的幅频率曲线图。

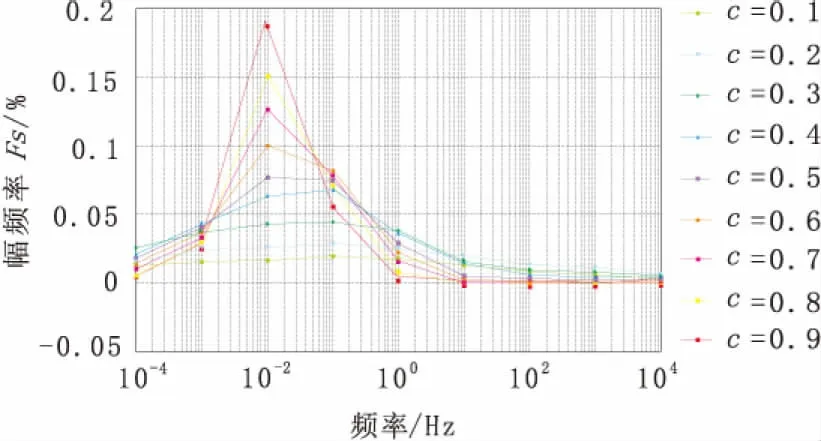
图6 不同频率相关系数对应的幅频率曲线(m=0.8,τ=50 s)Fig．6 Curves of Fs in different correlation coefficient(m=0.8,τ=50 s)

从图6可知，随着频率相关系数c2的增大，幅频率极值也相应变大，但在极值两翼上，幅频率表现出无规律的变化，幅频率的极值频率基本上与频率相关系数无关，故频率相关系数与幅频率除了在极值频率附近外，在其他频率段上相关性不大。

4 结论

在忽略电磁效应的情况下，通过用Cole-Cole模型的相应替换大地模型中的参数，与用有限单元法模拟伪随机激电法中的模型相应。通过分析伪随机激电法正演模拟的结果可知，模拟结果正确可靠，表明运用有限单元法模拟伪随机激电法中的参数是正确和适用的，为伪随机激电法的数值模拟进行了一些有益的尝试。

参考文献：

[1] 何继善.双频激电法[M].北京：高等教育出版社，2006.

[2] 徐世浙.地球物理中的有限单元法[M].北京：科学出版社，1994.

[3] 黄俊革.三维电阻率/极化率有限元正演模拟与反演成像[D].长沙：中南大学，2003.

[4] 傅良魁. 电法勘探教程[M].北京：地质出版社，1983.

[5] 傅良魁. 应用地球物理教程[M]．北京：地质出版社，1991.

[6] 李金铭. 电法勘探方法发展概况[J]. 物探与化探, 1996,20(4):93-95.

[7] 罗延钟,孟永良. 关于用有限单元法计算二维构造点电源场的几个问题[J].地球物理学报, 1986,29(1): 32-35.

[8] 周熙襄，钟本善. 电法勘探数值模拟技术[M]. 成都： 四川科学技术出版社, 1986.

[9] COGGON J H.Electromagnetic and electrical modeling by the finite-element method [J].Geophysics, 1971,36(1):132-155.

[10] 李大潜. 有限元素法在电法测井中的应用[M]. 北京：石油工业出版社，1980.