磁性源激发极化可行性讨论

杨 毅， 李桐林， 王大勇， 李建平， 张 辉

(1.中国地质科学院 地球物理地球化学勘查研究所,廊坊 065000;2.吉林大学 地球探测科学与技术学院,长春130026； 3.山东科技大学 地质学院, 青岛 266510；4.新疆库尔勒塔里木油田研究院 计算中心 ，库尔勒 841000)

0 引言

电磁法勘探是以岩、矿石的电性差异为物性前提的一种地球物理勘探方法，导电性差异和激电差异是其判断异常的依据，其中激电方法是上世纪七十年代发展起来的一种电法分支方法即复电阻率法(又称为频谱激电法(SIP))。多年来这种方法在金属硫化物类矿床勘察、地下水勘察、煤田勘察等领域取得众多成果，受到人们的广泛关注，值得特别指出的是，激发极化法在矿产普查勘探中发挥了重要作用，尤其对于其他物探方法难以奏效的低品位硫化物矿床，激发极化法能获得较好异常。

Hohmann[1]首先运用体积分方程方法在理论上对激发极化效应和电磁效应并存的异常响应问题进行了研究。Pelton[2]发表了激发极化法中运用多频发射信号来测量激电效应的文章，文中指出通过对多频信号的激电响应测量可以对不同类型的矿物进行区分，并指出这种方法对去除激发极化测量中的电磁耦合效应有明显改善，该篇文章的出现，奠定了复电阻率法的基础。Pelton[2]等通过对大量岩、矿石标本和露头的测量建立了基于激电效应的岩矿石模型，其数学表达式为：

上式称为Cole-Cole模型，其中ρ0为零频电阻率；m为极化率;τ为时间常数;c为频率相关系数。

在频谱激电正演研究方面，熊宗厚等[3]利用基于体积分方程的方法解决了复杂围岩条件下三维地质体激电效应和电磁效应并存的数值模拟问题。李晓波等[4]研究了层状大地中复电阻率异常体的激发极化效应和复电阻率响应问题。张辉等[5-7]利用积分方程法实现了均匀半空间中带三维复电阻率体的电磁场正、反演模拟以及井中基于磁性源的偶极-偶极三维异常响应模拟。蔡军涛等[8]使用有限元法进行了均匀大地中二维复电阻率电磁响应的数值模拟研究工作。张濡亮[9]使用积分方程法研究了复电阻率三维正演问题，计算了复电阻率异常体在不同Cole-Cole模型参数条件下的电磁响应并总结了响应规律。杨晓弘等[10]采用有限元法进行了频率域激电的数值模拟，给出了不同复电阻率模型条件下响应结果，并总结了规律。李建平等[11]利 用积分方程法实现了带地形条件下三维复电阻率体的电磁场正、反演模拟。王大勇等[12]采用体积分方程模拟了三维复电阻率体响应，并利用物理模型总结了响应规律。

目前对于频谱激电的研究都是基于电性源开展的。对于常规的激电方法来说，需要使用接地电极向地下供电，然后才能进行测量，这样必然就涉及到接地电阻问题，在现有条件下，如果接地电阻过大，只有加大发射功率以期获得较大二次场响应，但事实上，在戈壁、沙石地等高电阻覆盖层地区是很难实现的。实践证明，即使是现有的大功率发射机在新疆、内蒙戈壁上也很难获得较强的二次场信号。若使用不接地回线激发，即使用磁性源激发，不涉及接地电阻问题大小，则这个问题就会迎刃而解。关于使用磁性源激发极化的研究早在上世纪七十年代Hohman[13]就展开了理论和实际的研究，他利用一个频率域EM系统来测量与一次场正交的反转信号，其结果表明，IP效应在这个用振幅数据表示的系统中是探测不到的。Lee[14]研究了一个可极化球体在在自由空间中的响应。Spies[15]提出了TEM数据处理中负瞬变响应问题。Lee等[16-18]研究了极化全空间和半空间的响应。Weidelt[19]认为用非频散电阻率模型不能解释TEM中的负响应，他的观点推动了极化介质在TEM测量中影响规律的研究。Lewis等[20]计算了均匀半空间中二维可极化圆柱体的响应。A.P.Raiche等[21]利用Cole-Cole复电阻率模型对层状大地进行了TEM正演模拟，模拟结果在晚延时为负响应,这与TEM实际测量数据吻合，他们认为TEM在层状大地上的负响应是由于激发极化效应造成的。Flis[22]通过对复电阻率模型描述的层状介质的数值模拟讨论了激发极化效应对于瞬变电磁响应的影响，重点对时间常数和极化率两个参数变化的响应结果进行了讨论和比较，其数值模拟结果表明复电阻率模型条件下，瞬变电磁响应完全不同于实电阻率条件下响应，两种模型条件下响应的巨大差异警示我们，在模型建立的时候，应该充分考虑实际情况，而合理简化。

这里使用体积分方程的法计算了磁偶极源激发条件下复电阻率模型的响应，根据研究需要，设计了多个不同复电阻率和实电阻率模型的组合模型，对相应结果进行了计算，最后引入磁荷概念对电磁响应结果进行了分析总结了磁性源激发条件下Cole-Cole模型参数对复电阻率异常体的电磁感应效应和激发极化效应的影响规律，在理论上证明了磁源激发极化的可行性。

1 磁源复电阻率三维模拟结果及分析

为了研究磁偶极子激发条件下，不同Cole-Cole模型参数对复电阻率异常体激发极化效应与电磁感应效应的影响规律，我们设计了如下地电模型(图1)。

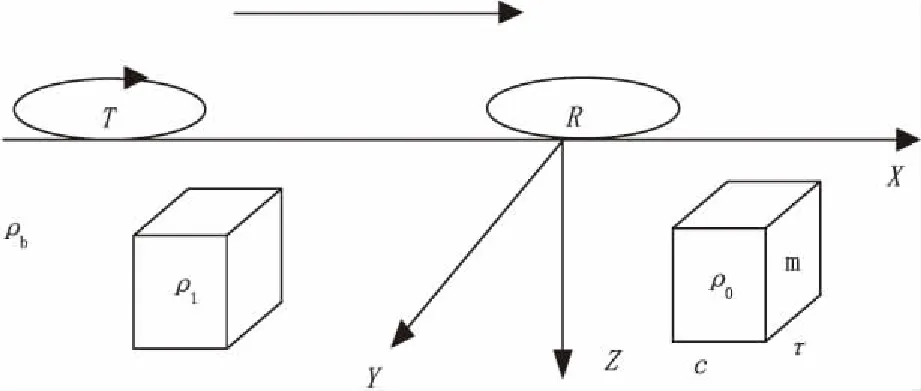
图1 磁偶极子源激发均匀大地中三维异常体模型Fig．1 Model of 3D anomaly body in homogeneous earth stimulated by magnetic dipole source

在图1中，模型设计为：背景为均匀半空(非复电阻率)，电阻率为100 Ω·m，在其间放置两个三维电阻率异常体，边长均为100 m×100 m×100 m，其中左面异常体中心点坐标为(-300，0，150)，电阻率为ρ1=20 Ω·m，右面是异常体复电阻率异常体，其中心点坐标为(300，0，150)。激发源磁矩m=1 A·m2，激发源起始坐标为(-600，0，0)。在计算时，将模型中的异常体按小立方块进行剖分后，把Cole-Cole模型参数赋给每一个小立方块，按电磁散射理论，计算地表观测点响应，并分析Cole-Cole参数变化对计算结果的影响。

图2和图3表示表示模型中复电阻率异常体零频电阻率分别为为5 Ω·m、20 Ω·m、50 Ω·m、100 Ω·m、1000 Ω·m、2000 Ω·m时在x方向上计算得到的二次垂直磁场响应，其他参数为：m=0.6、τ=100 s、c=0.25，激发源工作频率为1 Hz。其剖面布设图如图1所示，发射偶极子起始位于x轴-500 m处，接收起始位于-400 m处，接收发射间距为100 m，整个系统从负半轴向正半轴移动，发射移动至550 m处，接收移动至650 m处。

特别说明的是，本次研究采用积分方程法可以直接得到异常体的响应，下面提到的二次场均为异常体响应。为简化研究，只讨论低频1Hz情况下异常体的垂直磁场响应。

从图2和图3中可知，二次磁场垂直分量实部在复电阻率体上方场值均为负值，电阻率在5 Ω·m～100 Ω·m时，幅值随零频电阻率增大而增大，在高阻时随零频电阻率增大而减小；虚部幅值在零频电阻率小于背景电阻率时为正值，并且随零频电阻率增大而减小，在复电阻率异常体为高阻时二次场垂直分量幅值表现为负值，并且幅值强度随零频电阻率增大而增大。

图2 不同零频电阻率时二次磁场z分量实部沿x轴变化曲线Fig．2 Variations along axis "x" of Hz real parts of secondary magnetic field under different zero frequeccy resistivity

图3 不同零频电阻率时二次磁场z分量虚部沿x轴变化曲线Fig．3 Variations along axis "x" of Hz imaginary parts of secondary magnetic field under different zero frequeccy resistivity

为了详细研究电阻率的变化对其正上方二次场实部和虚部的影响，设计了如下模型(图4)，将图1模型中右侧复电阻率异常体变为实电阻率异常体，考虑到突出部分背景，将发射和接收整体向x轴负向移动50 m。

不同实电阻率时二次磁场垂直分量实部沿x轴变化曲线(图4)表明：由于电磁感应作用，低阻异常体使得电磁波不容易通过，于是异常体在电磁波入射一侧出现正磁荷，另一侧则出现负磁荷，其等效作用相当于一个磁偶极子，且磁偶极子场的方向与外场方向相反。实际上随着源的移动，等效磁偶极子将发生转动(这里只给出了发射源固定于某一位置的讨论结果)，于是在低阻异常体两侧出现负异常，低阻异常体正上方出现正异常且电阻率越低，异常强度越大；高阻相反，在异常体正上方出现负异常，两侧出现正异常，且电阻率越高，异常强度越大。需要说明的是，由于记录点设置在接收线圈中心，所以异常中心向收发装置移动方向偏移半个收发距。

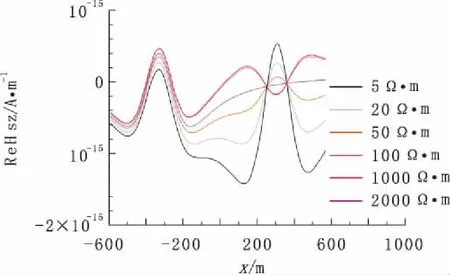
图4 不同实电阻率时二次磁场z分量实部沿x轴变化曲线Fig．4 Variations along axis "x" of Hz real parts of secondary magnetic field under different real resistivity

不同实电阻率时二次磁场z分量实虚部沿x轴变化曲线(图5)表明：二次磁场实虚部也是由于电磁感应造成的，并且电磁感应发生时，我们认为一次场实部通过异常体感应产生了二次场虚部，一次场虚部过异常体感应产生了二次场实部，而在在低频条件下，一次磁场实部远大于虚部，所以，二次场幅值实部小于虚部。

由此可知，在图2和图3中，因为存在激电效应，故二次场实虚部响应曲线随ρ0变化并不规则；并且通过对比(图3和图5、图2和图4的对比)，当复电阻率异常体零频电阻率值与半空间背景电阻率值一致时所受激电效应影响最为显著。为进一步研究磁性源激电效应的规律，明确其机理，将图1中右侧用Cole-Cole模型表示的异常体变为实电阻率异常体，并与Cole-Cole模型表示的异常体进行对比。具体参数变化如下：图1中右侧异常体设为电阻率为50 Ω·m的实电阻率和复电阻率分别计算各自响应，结果如图6和图7所示，又将图1右侧异常体设为电阻率为1 000 Ω·m的相对高阻实电阻率和复电阻率分别计算各自响应，结果如图8和图9所示。

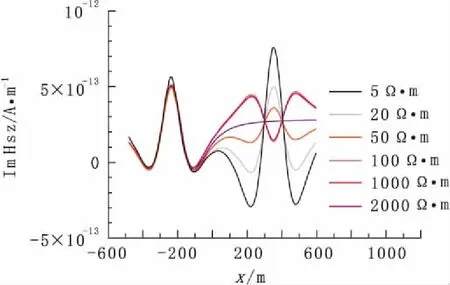
图5 不同实电阻率时二次磁场z分量虚部沿x轴变化曲线Fig．5 Variations along axis "x" of Hz imagi-nary parts of secondary magnetic field under different real resistivity

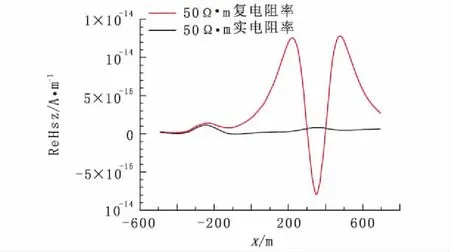
图6 实电阻率和复电阻率零频电阻率都为50 Ω·m时二次磁场z分量实部沿x轴变化曲线Fig．6 Variations along axis "x" of Hz real parts of sec-ondary magnetic field under real resistivity and imaginary resistivity are 50 Ω·m

从图6和图8可以看出，对于实电阻率异常体，由于其极化率为零，所以其异常变化是由电磁感应引起的，其表现形式为异常体电阻率低于背景时，表现为排斥磁流，异常体电阻率高于背景则表现为吸引磁流。而复电阻率二次场实分量幅值较相同零频电阻率的实电阻率二次场实分量要大，且对于低阻，复电阻率二次响应甚至反号(图6)，这是因为激发极化效应发生，影响了二次场实部曲线。这里我们将磁源激发极化效应用类似于电容效应的‘磁容效应’来解释，即激发极化发生时，在入射波一侧的异常体边界上负的磁荷累积，另一侧正的磁荷累积，这个过程相当于充磁，其作用等效于一个磁偶极子，并且随着发射源和接收线圈的移动，磁偶极子发生转动，其作用结果使得二次磁场垂直分量实部在异常体上方负向增加。于是对于低阻体，激发极化使得二次磁场垂直分量实部幅值减小，甚至反号；对于高阻体则使得其二次场垂直分量实部幅值增大。

图7 实电阻率和复电阻率都为50 Ω·m时二次磁场z分量虚部沿x轴变化曲线Fig．7 Variations along axis "z" of Hz imag inary parts of secondary magnetic field under real resistivity and imaginary esistivity are 50 Ω·m

图8 实电阻率和复电阻率都为1 000 Ω·m时二次磁场z分量实部沿x轴变化曲线Fig．8 Variations along axis "x" of Hz real parts of secondary electric field under real resistivity and imaginary resistivity are 1 000 Ω·m

由图7和图9可见，实电阻率二次场虚部变化也是由于电磁感应的影响，低阻排斥磁流，高阻吸引磁流，而复电阻率二次磁场虚分量较相同零频电阻率的实电阻率二次场虚分量发生了变化，我们将这一现象解释为电磁感应，但这是由于异常体反抗激发极化产生而产生的，所以将这一效应称之为极化感应效应。磁荷在入射波一侧的异常体边界上累积正的磁荷，另一侧累积负的磁荷，以反抗激发极化的磁荷累积，其作用等效于一个磁偶极子，并且随着发射源和接收线圈的移动，磁偶极子发生转动，其作用使得二次磁场垂直分量虚部在异常体上方正向增加。于是对于低阻体，极化感应使得二次场垂直分量虚部幅值增加，而对于高阻体，使得二次场垂直分量虚部幅值减小。

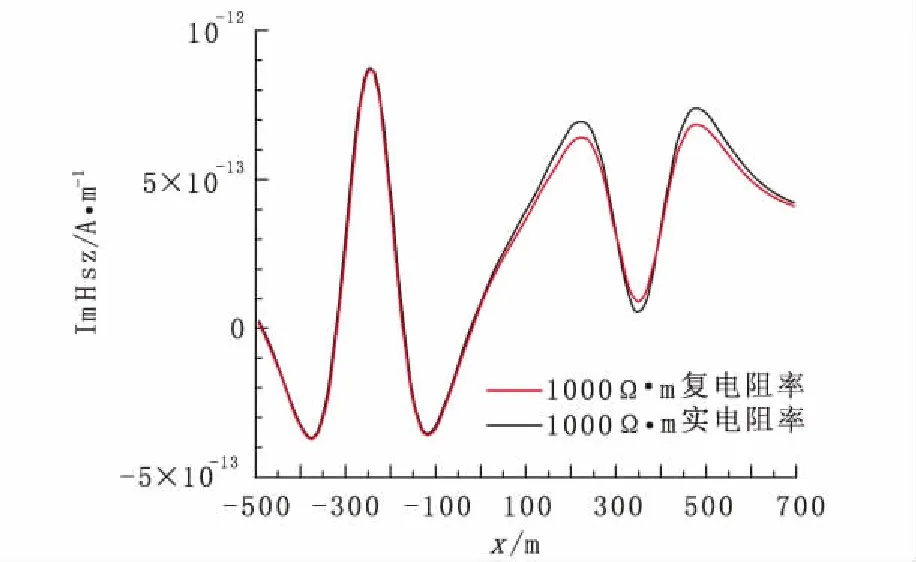
图9 实电阻率和复电阻率都为1 000 Ω·m时二次磁场z分量虚部沿x轴变化曲线Fig．9 Variations along axis "x" of Hz imaginary parts of secondary electric field under real resistivity and imaginary resistivity are 1 000 Ω·m

基于以上的模拟结果，作者考虑了这样一个解释模型如图10、图11来解释磁源复电阻率二次场。

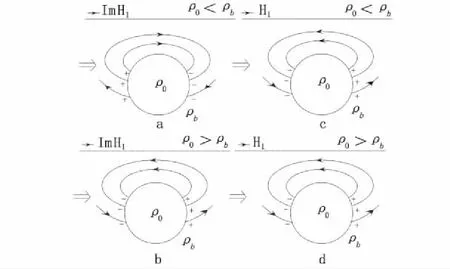
图10 正演结果中二次磁场实部模型Fig．10 Models of real parts of secondary magnetic field in forward results response(a)、(b)电磁效应；(c)、(d)激电效应

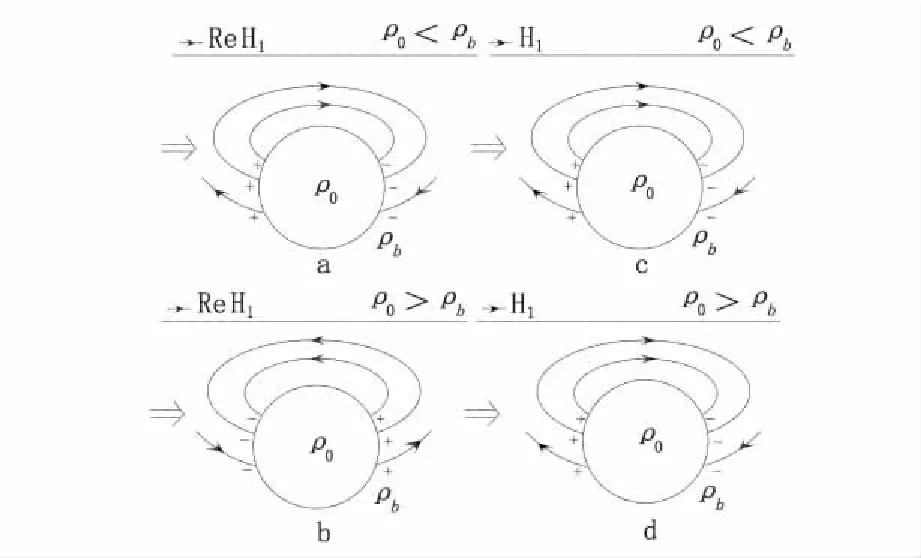
图11 正演结果中二次磁场虚部模型Fig．11 Models of imaginary parts of secondary magnetic field in forward results response(a)、(b)电磁效应；(c)、(d)感应激发极化

二次场的实部主要电磁感应和激发极化的影响。电磁感应使得低阻异常体相当于一个吸引磁流的磁偶极子，高阻异常体相当于一个排斥磁流的磁偶极子，且随着收发装置的移动，异常体等效偶极子也发生转动，最后使得低阻异常体上幅值为负，两侧为正，高阻异常体上幅值为正，两侧为负，且异常体电阻率值与背景差异越大，响应越强(图11(a)，图11(b))。发生激发极化时，异常体(不论高低阻)相当于一个排斥磁流的磁偶极子，且随着收发装置的移动，异常体等效偶极子也发生转动，最后使得异常体上幅值为正，两侧为负(图10(c)、图10(d))。

2 结论

综合以上分析，可以得出如下结论：

(1)正演结果分析表明，磁性源激发条件下，三维复电阻率体的电磁响应是由电磁感应和激电效应共同产生的。在磁源激发条件下，二次磁场的激发极化效应是明显的，磁源激发条件下的激发极化法是可行的。

(2)二次场的虚分量由电磁感应和感应激发极化共同影响。电磁感应作用与实部一致，感应激发极化也是，要说明的是感应激发极化是由于异常体反抗激发极化效应造成的。

(3)当地下异常体为低阻极化异常体时，同电性源激发极化一样，此时异常体内的电磁感应效应和激发极化效应响应方向相反，表现为相互抵消，两者互为干扰，其影响强弱随频段变化。低频时，激发极化效应较强，高频时，电磁感应较强，在实际工作中根据工作频段应考虑其产生的影响。

(本次研究仅进行了磁偶源复电阻率模型的正演模拟以及垂直磁场规律总结研究，未对电场和水平磁场的规律进行总结，而时间域的复电阻率响应也正在研究中。)

参考文献：

[1] HOHMANN G W. Three dimensional induced polarization and electromagnetic modeling [J]. Geophysics，1975, 40(2):309-324.

[2] PELTON W H, WARD S H, HALLO F P, et al. Mineral discrimination and removal of inductive coupling with multrfrequency IP[J]. Geophysics， 1978, 43(3): 588-609.

[3] XIONG Z, LUO Y, WANG S,et al. Induced-polarization and electromagnetic modeling of a three-dimensional body in a two-layer anisotropic earth [J]. Geophysics,1986,51:2235-2246.

[4] 李晓波, 朴华荣. 两层大地中三维体的激发极化与电阻率响应的积分方程模拟[J]. 地球物理学报,1988, 31(3): 342-352.

[5] 张辉, 李桐林, 董瑞霞. 基于电偶源的体积分方程法三维电磁反演[J]. 吉林大学学报:地球科学版,2006, 36(2):284-288.

[6] 张辉, 李桐林, 董瑞霞. 体积分方程法模拟复电阻率三维体电磁响应[J]. 煤田地质与勘探,2006，34(1):70-73.

[7] 张辉, 李桐林, 董瑞霞. 体积分方程法模拟电偶源三维电磁响应[J]. 地球物理学进展,2006, 21(2):386-390.

[8] 蔡军涛, 阮百尧, 赵国泽, 等. 复电阻率法二维有限元数值模拟[J].地球物理学报,2007, 50(6): 1869-1876.

[9] 张濡亮. 复电阻率三维正演问题研究[D]. 北京：中国地质大学,2008.

[10] 李建平. 带地形的三维复电阻率电磁场正反演研究 [D].长春：吉林大学,2008.

[11] 杨晓弘，何继善，童孝忠. 频率域激电有限元数值模拟[J]. 地球物理学进展,2008, 23(4):1186-1189.

[12] 王大勇，李桐林. 三维复电阻率模型电磁场正演模拟研究[J].地球物理学进展.2010, 25(1):266-271.

[13] HOHMANN G W, KINTZINGER P R, VAN VOORHIS G D, et al.Evaluation of the measurement of induced electrical polarization with an inductive system. Geophysics. 1970, 35:359-915.

[14] LEE T J, Sign reversals in the transient method of electrical prospecting (one-loop version) [J]. Geophys,Prosp,1975, 23: 453-462.

[15] SPIES B R. A held occurrence of sign reversals with the transient EM method[J]. Geophys,Prosp. 1980, 28: 620-632.

[16] LEE T J.Transient electromagnetic response of a polarizable ground[J]. Geophysics,1981, 46:1037-1041.

[17] RNLCHE A P. Negative transient voltage and magnetic field responses for a half-space with Cole-Cole impedance[J]. Geophysics,1983, 48: 790-791.

[18] WAIT J R, Debroux P. Induced polarization in electromagnetic inductive schemes[J]. Geophys, Prosp, 1984, 32:1147-1154.

[19] WEIDELT P. Response characteristics of coincident-loop transient electromagnetic systems[J].Geophysics. 1982, 47:1325-1330.

[20] LEWIS J G, LEE T J. The detection of induced polariration with a lransient electromagnetic system[J]. Inst. Elect. Electron.Eng.. Trans. Geosci. Remote Sensing, 1984, 22:69-80.

[21] RAICHE A P, BENNETT L A, Clark P J ,et al. The use of ColeCole impedances to interpret the TEM response of layered earths[J]. Expl. Geophys,1985, 16:271-272.

[22] FLIS M F,NEWMEN G A,HOHMANN G W.Induced-polarization effect intime-domain electromegnetic measurements[J] Geophysics,1989, 54(4):514-523.