基于各向异性高斯方向导数滤波器的角点检测

章为川,张 智,赵 强，高 燚

(西安工程大学 电子信息学院,陕西 西安 710048)

角点是图像基本特征之一,包含了丰富的结构信息,并且具有几何变换不变性.角点检测是图像处理和计算机视觉重要的组成部分,在图像配准、三维重建及目标跟踪与识别中具有重要的作用[1-4],现今存在大量的角点检测方法.角点一般被认为是图像中周围灰度变化剧烈的点[5]或者图像边缘曲线上曲率极大值的点[6],因此角点检测算法大致可以分为两类:基于图像灰度的角点检测算法[6-9]和基于边缘轮廓的角点检测算法[10-15].基于图像灰度的角点检测算法利用一阶或者二阶微分算子检测角点,由于二阶微分算子对噪声非常敏感,因此大多采用一阶微分算子提取角点.Moravec[7]提出了直接从图像中检测角点的算法,该算法计算简单,运行速度快,但对噪声敏感.Harris等对其进行了改进,得到经典的Harris角点检测算法[6].Harris算法首先利用图像的一阶导数估计局部梯度自相关矩阵,然后根据自相关矩阵的特征值来判定像素点是否为角点.Harris算法检测角点可靠性较高,具有一定旋转平移不变性,是现今图像特征匹配中常使用的角点检测算法,但同性高斯核函数对噪声敏感,Harris检测算法角点定位性不好.基于边缘轮廓的角点检测算法主要是通过分析图像边缘的形状特性来检测角点.这种方法首先提取图像的边缘轮廓(如Canny算子[16]),然后从边缘中提取封闭或者非封闭的边缘轮廓曲线,最后通过搜索轮廓线上的曲率局部极大值点,或者斜率或梯度方向变化点,或者利用多边形逼近,然后搜索交叉点来提取角点.基于边缘轮廓线的角点检测算法依赖图像边缘提取,若提取的边缘线出现断裂现象,则会对角点提取产生重要影响[13],边缘线的定位性也影响角点定位能力.其次,基于边缘轮廓线的角点检测需要计算曲率来判定角点,对噪声非常敏感,同时用于平滑边缘线的高斯函数尺度的选择[17]也是个难题.

为了改进Harris算法[6]存在的缺陷,本文提出了利用ANDD滤波器直接在图像上进行角点检测的算法.首先用ANDD滤波器组对图像作平滑处理,再利用邻域像素各向异性方向导数计算自相关矩阵建立角点测度提取角点.

1 角点检测算法

首先介绍各向异性高斯核及其方向导数滤波器,然后分析各向异性高斯方向导数的噪声鲁棒性,并给出其离散化形式,最后描述本文算法.

1.1 各向异性高斯核及其方向导数

拉长二维高斯核函数[18]可以表示为

(1)

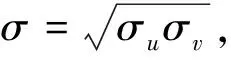
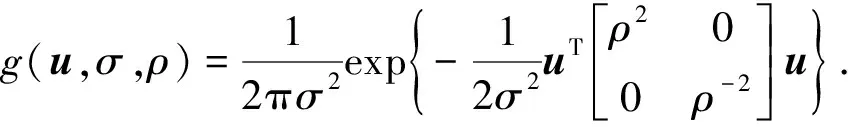
(2)

其中u=[u,v]为直角坐标系坐标,对式(2)中x变量求导即可得到二维高斯核函数一阶微分算子:

(3)

通过分别逆时针旋转式(2)和式(3)可得到不同方向各向异性高斯核函数及其方向导数的表达式:

(4)

图1 各向异性高斯方向导数滤波器(σ2=ρ2=6, θk=k×180°/8, k=1, 2,…,8)

其中Rθ为旋转矩阵,θ为旋转角度.图1为8个方向各向异性高斯方向导数滤波器.各向异性高斯核函数作用于图像对应于不同方向的平滑,各向异性高斯方向导数可以较好地提取图像多尺度多方向灰度变化信息[18].因此可以利用各向异性及角点特性[17]来建立角点测度进行角点检测.

图2为边缘模型与各角点模型.第一行分别显示了图像阶跃边缘(a)、L型角点(b)、Y型角点(c)和X型角点(d)的角点模型,第二行分别为几种图像特征对应的各向异性高斯方向导数滤波器响应的幅值响应,第三行分别为几种图像特征对应的各向同性高斯方向导数滤波器响应的幅值响应.由图2可以看出利用各向异性高斯方向导数能够很好提取图像多方向的灰度变化信息,很容易区分边缘和角点,这是各向同性高斯核函数一阶导数不能做到的,这与文献[18]说明相一致.

1.2 导数抑制噪声能力及其离散化

图像在传输和接收过程中不可避免的会被噪声污染.假设图像被零均值方差的高斯白噪声污染,则含噪图像经尺度为σ,各向异性因子为ρ的各向异性高斯方向导数滤波器平滑后噪声的方差[18]为

(5)

由此可以看出各向异性高斯方向导数滤波器不仅可以提取图像多方向灰度变化信息,还具有一定噪声抑制能力.实际中图像是离散的,通常需要对连续各向异性高斯方向导数作离散采样处理,方向角也应进行离散化,如式(6)所示.

(6)

则图像各向异性方向导数滤波器响应为

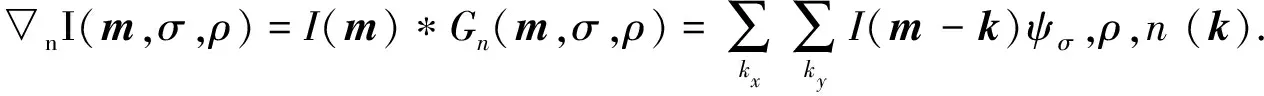
(7)

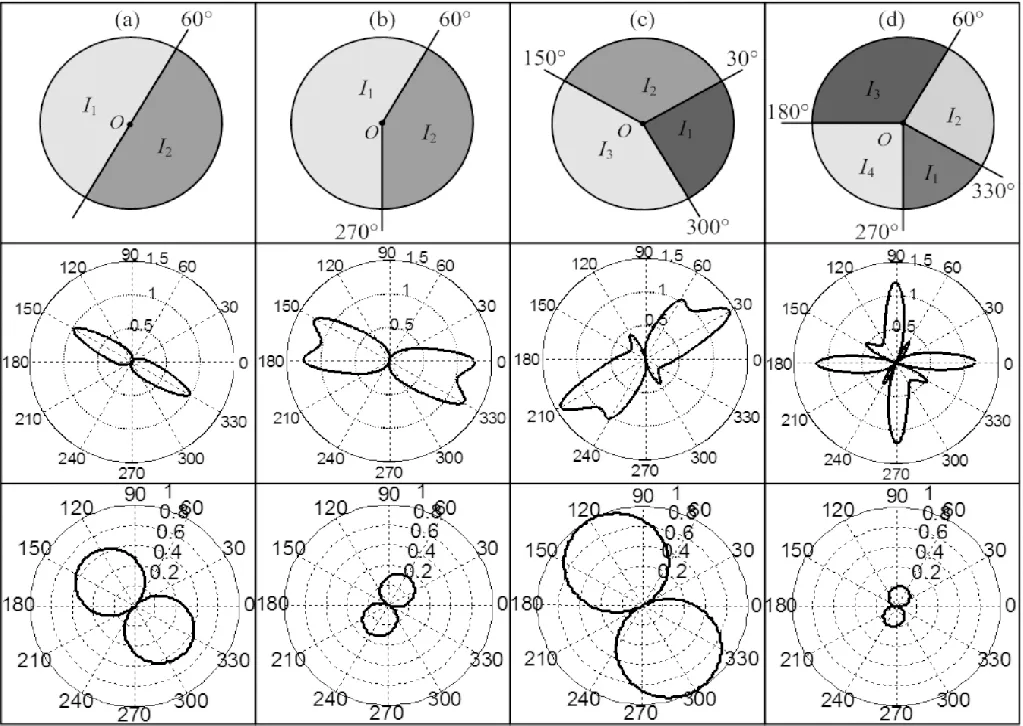
图2 边缘模型与角点模型

1.3 算法设计

利用各向异性高斯方向导数构成一组滤波器对图像进行平滑处理,根据图像像素与周围邻域像素点的各向异性方向导数响应构造自相关矩阵,利用自相关矩阵特征值建立角点测度从而提取角点.

(1) 角点测度 基于边缘轮廓线的检测算法角点测度基于边缘,而角点包含信息不止与自身有关也与周围邻近像素有关[17],利用各向异性高斯方向导数滤波器可以获取像素的不同方向的灰度变化信息.同时，定义了新的提取角点的角点测度.

对于每一个像素点,利用该像素点及其邻域的P个方向的各向异性方向导数滤波器响应构造矩阵,若邻域取3×3,则矩阵为9×P的矩阵如式(8):

(8)

令∑m=M(m)TM(m) 表示各向异性方向导数滤波器响应的局部自相关矩阵,可以看出该矩阵为对称矩阵,其特征值均为非负实数.自相关矩阵特征值可以用来判定角点[8].特征值均很大,表示该像素点处灰度变化剧烈,该点为角点;特征值有大有小,则为边缘点;特征值均很小则为平坦区域点.对每个像素点处的P个特征值做归一化处理，得到归一化的特征值，即

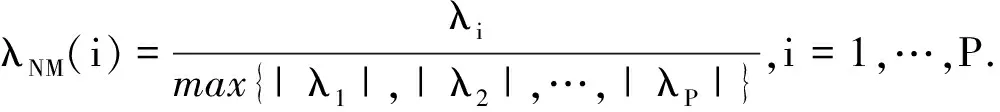
(9)

归一化特征值的乘积可以反映特征值大小,同时求取每个像素点处各向异性方向导数响应的幅值平方和的归一化值G(m),则新的角点测度定义为

(10)

(2) 算法流程 (a) 利用各向异性高斯方向导数对输入图像进行平滑滤波,得到图像各个方向响应;(b) 对于图像每个像素点计算局部自相关矩阵,计算其特征值并做归一化处理,根据归一化特征值及滤波器响应平方和的归一化值建立角点测度;(c) 若大于预先设定阈值,则将该像素点判定为候选角点;(d) 对候选角点进行非极大值抑制处理,若在某一邻域内(如5×5)该点测度为极大值则标记为角点.

图像角点处的灰度变化信息是各向异性的[21],角点与邻域像素之间相关性不强,本文算法利用了邻域像素之间相关性,根据设定阈值即可检测角点.

2 结果与分析

通过对积木和实验室图像在无噪和加噪声条件下进行角点检测来比较本文提出的算法和Harris角点检测算法，图3为实验所用积木和实验室参考角点图(图中角点用小四方块标记).两幅图像分别有59,249个真实角点.实验中各向异性高斯方向导数P=8，尺度因子和各向异性因子均取值为2，测度阈值为0.001.分别选取邻域3×3,5×5,7×7,9×9,11×11，经过多次实验比较，选取7×7邻域时角点错检数和漏检数均最小，3×3检测效果次之.但同时邻域窗的增大会使计算量增加，为了降低计算复杂度，实验中选取3×3邻域计算自相关矩阵.

(a) 积木图像的参考角点图 (b)实验室图像的参考角点图图3 参考图像和真实角点图

采用文献[12]描述的准则评价算法性能,假设CDC为检测器检测角点集合,CGT为参考角点集合,若CGT中角点Ci与CDC中角点距离最小值不大于预定距离DMAX(实验中DMAX=4),则Ci标记为正确检测的角点,并记最小距离为di,否则角点Ci标记为漏检角点,CDC集合中除去匹配的角点外其他角点标记为错检角点.定位误差Le定义为所有正确匹配角点距离误差的平均值.表1和表2分别给出了算法在无噪和加噪条件下的检测结果,其中表2是加零均值方差为100的高斯白噪声进行100次实验的平均结果.

由表1和表2可以看出,与经典Harris角点检测算法相比,本文提出的算法具有更好的检测性能,在3个性能指标上都优于Harris角点检测算法,检测性能分别提高了6.8%,5.2%,无噪声和加噪情况下定位误差的对比可以看出本文的算法噪声鲁棒性优于Harris算法.对于复杂的图像(如实验室图像),对角点检测算法要求较高因此会产生较多的漏检角点和错检角点.与Harris角点检测算法相比,本文算法在无噪和含噪声情况下具有更好的检测.

表1 无噪声下两种方法实验图像角点匹配结果比较

3 结束语

基于角点的定义,提出一种利用各向异性方向导数滤波器构造局部自相关矩阵的角点检测算法.该算法既能提取图像多方向灰度变化信息,还可以很好的定位角点.通过对比实验，本文算法优于经典的Harris角点检测算法.

参考文献：

[1] MOHAMMAD A,GUOJUN LU.An improved curvature scale-space corner detector and a robust corner matching approach for transformed image identification[J].IEEE Trans.Image Processing,2008,17(12):2425-2441.

[2] YKRYSTAN M,CORDELIA S.Scale & affine invariant interest point detectors[J].International Journal of Computer Vision,2004,60(1):63-86.

[3] L KITCHEN,A ROSENFELD.3-D model localization using high-resolution reconstruction of monocular image sequences [J],IEEE Trans.Image Processing.1997,6(1):175-188.

[4] BRETZNER L,LINDERERG T.Feature tracking with automatic selection of spatial scales[J].Computer Vision and Image Understanding,1998,71(3):385-392.

[5] SMITH S M,BRADY J M.SUAN-A new approach to low level processing[R].TR95SMSlC,UK:Oxford University,1995.

[6] C HARRIS,M STEPHENS.A combined corner and edge detector[C].Proceedings of the 4th Alvey Vision Conference,England,1988,pp.147-151.

[7] H P MORAVEC.Towards automatic visual obstacle avoidance[C]//Proceedings of the 5th Intrnational Joint Conference Artificical Intelligence,Cambridge,1977:584.

[8] 章为川,程冬,朱磊.基于各向异性高斯核的多尺度角点检测[J].电子测量与仪器学报,2012,26(1):37-42.

[9] NOBLE J A.Finding corners[J].Image and Vision Computing,1988,6(2):121-128.

[10] MOKHTARIAN F,SUOMELA R.Robust image corner detection through curvature scale space[J].IEEE Trans.on Pattern Analysis and Machine Intelligence,1998,20(12):1376-1381.

[11] XIAO C HE,N H C YUNG.Corner detector based on global local curvature properties[J].Optical Engineering,2008,47(5):1-8.

[12] MOHAMMAD A,GUOJUN LU.Robust image corner detection based on the chord-to-point distance accumulation technique[J].IEEE Transactions on Multimedia,2008,10(6):1059-1072.

[13] SHUI Peng-Lang,ZHANG Wei-chuan.Corner detection and classification using anisotropic directional derivative representations[J].IEEE Transaction Image Processing,2013,22(8):3204-3218.

[14] 章为川,水鹏朗,朱磊.利用各向异性高斯方向导数相关矩阵的角点检测方法[J].西安交通大学学报,2012,46(11):91-97.

[15] 章为川,水鹏朗,徐国靖.边缘线上各向异性高斯核信息熵的角点检测[J].西安电子科技大学学报,2013,40(4):119-125.

[16] CANNY J.A computational approach to edge detection[J].IEEE Transaction Pattern Analysis Machine Intelligence,1986,8(6):679-698.

[17] 章为川.基于各向异性高斯核的图像边缘和角点检测[D].西安：西安电子科技大学,2013:32-40.

[18] SHUI P L,ZHANG W C.Noise-robust edge detector combining isotropic and anisotropic Gaussian kernels [J].Pattern Recognition,2012,45(2):806-820.

[19] RYU J B,LEE C G,PARK H H.Formula for Harris corner detector[J].Electronics Letters,2011,47(3):180-181.