一种基于邦戎表的船台下水计算程序开发与应用
2014-06-27,,
, ,
(泰州口岸船舶有限公司,江苏 泰州 225321)
下水是船厂生产的一个重大节点,是船舶岸上建造和水下安装的分水岭,下水前应进行下水计算,预测下水的安全性,从而采取相应措施来保证船舶的顺利下水。
目前本公司采用《船舶性能计算》(CTJS)软件中的下水模块和手工计算两种方式计算船舶下水。CTJS下水计算需要输入整船的型值表,相当费时间,并且计算中发现有一些缺陷,如站数取值有限制,水位高于或低于某界限值容易报错等,另外对于双艉和倾斜龙骨的船型也不能进行计算。而手工计算则需要花费大量时间进行重复计算,出错率较高。为此,考虑直接采用邦戎表,取消以往的型值输入。
1 下水计算原理
根据船舶下水过程中运动的特点、作用力的变化以及可能发生的危险情况, 通常把纵向下水分为4个阶段[1]进行分析研究。
1)第一阶段。自船舶开始下滑至船体艉端接触水面为止。在这一阶段中, 船的运动平行于滑道。船舶船台方向仅受重力和滑动摩擦力,可以认为是做匀加速运动。计算出下滑加速度,即可以求出各滑程速度、时间。
2)第二阶段。自船体艉端接触水面至船艉开始上浮为止。在这一阶段中, 船的运动仍平行于滑道,随着船滑程增大,入水体积不断变大,浮力对艏支点力矩等于重力对艏支点力矩时,船艉开始浮起,称为艉浮。在下水的第二阶段中, 必须注意是否会发生艉跌落现象。当船的重心已在滑道末端之后, 而船艉尚未浮起时,如果重力对滑道末端力矩大于浮力对滑道末端力矩,则船以滑道末端为支点而发生艉下落现象,此时反力集中于滑道末端, 使船受到损伤。
此阶段船仍平行于滑道,可以确定船舶滑行某一距离x时的艏艉吃水,在邦戎曲线图上画出相当于上述不同行程x时的水线,然后用数值积分法算出每一水线下的浮力及浮心纵向位置, 据此可进一步分别求出浮力对于前支点及滑道末端的力矩,根据下水重量及重心位置, 可算出重力对于前支点及滑道末端的力矩,从而可以计算出艉浮滑程,并判断是否发生艉跌落现象。
3)第三阶段。自船艉开始上浮至下水架滑板前端离开滑道为止,称为全浮。该阶段必须注意是否发生艏跌落现象。当艏支点离开滑道末端时,浮力还小于重力,船艏吃水小于船自由浮起时的艏吃水,船艏会跌落,船艏或下水架可能由于碰击船台或河底而引起损伤。
此阶段龙骨和滑道不平行,可以假设多个龙骨坡度,根据艏支点吃水确定水线,查邦戎表积分得浮力、浮心位置,利用重力和浮力对艏支点力矩相同条件算出该阶段各滑程平衡时状态。根据全浮条件浮力等于重力计算出全浮滑程。
第二、第三阶段速度计算[2]公式为
(1)
式中:vi-1——上滑程末速度,m/s;
W——下水重力,kN;
Di——平均浮力,kN;
K——速度系数,通常取0.013;
△s——计算步长;
β——船台坡度;
fD——滑动摩擦系数;
g——重力加速度,m/s2。
(4)第四阶段。自下水架前支点离开船台滑道至船舶停止运动为止。该阶段,浮力等于重力,
利用式(1)可以计算出全浮后冲程。
综上,下水计算主要是计算各阶段滑程、速度,并判断是否发生艉跌落或艏跌落的危险情况。从而根据可能发上的危险状况作出相应改进措施,保证船舶下水安全。
2 下水程序计算流程和方法
2.1 程序计算流程
程序计算也是按下水阶段划分的。
具体流程见图1。
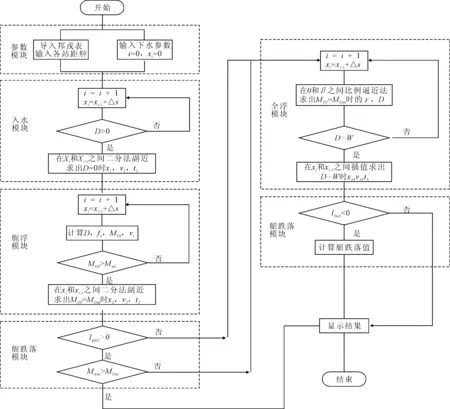
x为滑程;△s为计算步长;D为浮力;W为重力;t为时间;fx为浮心位置;v为速度;β为船台坡度;MDf为浮力对艏支点力矩;MWf为重力对艏支点力矩;MDm为浮力对滑道末端力矩;MWm为重力对滑道末端力矩;lgm2为艉浮时重心在滑道末端前距离;lfm3为全浮时艏支点在滑道末端前距离图1 程序计算流程
2.2 关键算法
2.2.1 利用贝塞尔曲线拟合法求浮力
通常计算排水量是利用邦戎表根据各站吃水查出各站面积(x1,a1),(x2,a2),…,(xn,an),x是各站距船舯距离,a为各站面积,然后利用数值积分法(如辛普森法积分)算得排水量。而本程序是通过对以上一组点拟合出三阶贝塞尔曲线方程[3]a=f(x),是三次多项式,
(2)

(3)
式中:xa、xf——艉站和艏站距船舯距离。
2.2.2 全浮计算模块
第三阶段,船艉离开滑道,要假设龙骨坡度γ,算得浮力对艏支点力矩MDf等于重力MWf时可得各滑程平衡状态。龙骨坡度γ在0和船台坡度β之间,由于排水量对于γ的变化比较敏感,采用二分法逼近效率比较低,故采用比例逼近法。本程序采用vb编写,全浮计算模块具体如下。
某一滑程x
d=dfz(x)
’艏支点吃水
r1=0:r2=0.05
’龙骨坡度界限
r0=(r1+r2)/2
M1=fuli(d,r1)
’求浮力矩函数,参数为艏支点吃水和龙骨坡度
M2=fuli(d,r2)
M0=fuli(d,r0)
Do Until Abs(M0-zlj)<1
’zlj为重力矩,浮力矩等于重力矩循环结束
If D0>0 Then
r2=r0
M2=M0
else
r1=r0
M1=M0
End if
r0=r1+(zlj-M1)/(M2-M1)*(r2-r1)
’比例插值龙骨坡度
M0=fuli(d,r0)
Loop
r=r0
’求得滑程x时的龙骨坡度,之后可求出浮力
2.2.3 本程序的优点
1)邦戎表导入界面是嵌入excel的OLE容器,操作和在excel里面一样,可以复制粘贴,方便快捷。邦戎表输入界面见图2,双击表格区域即进入编辑模式,第一行输入站号,第一列输入吃水,中间区域为各站对应吃水的横剖面积。保存后,程序会以此为参数。
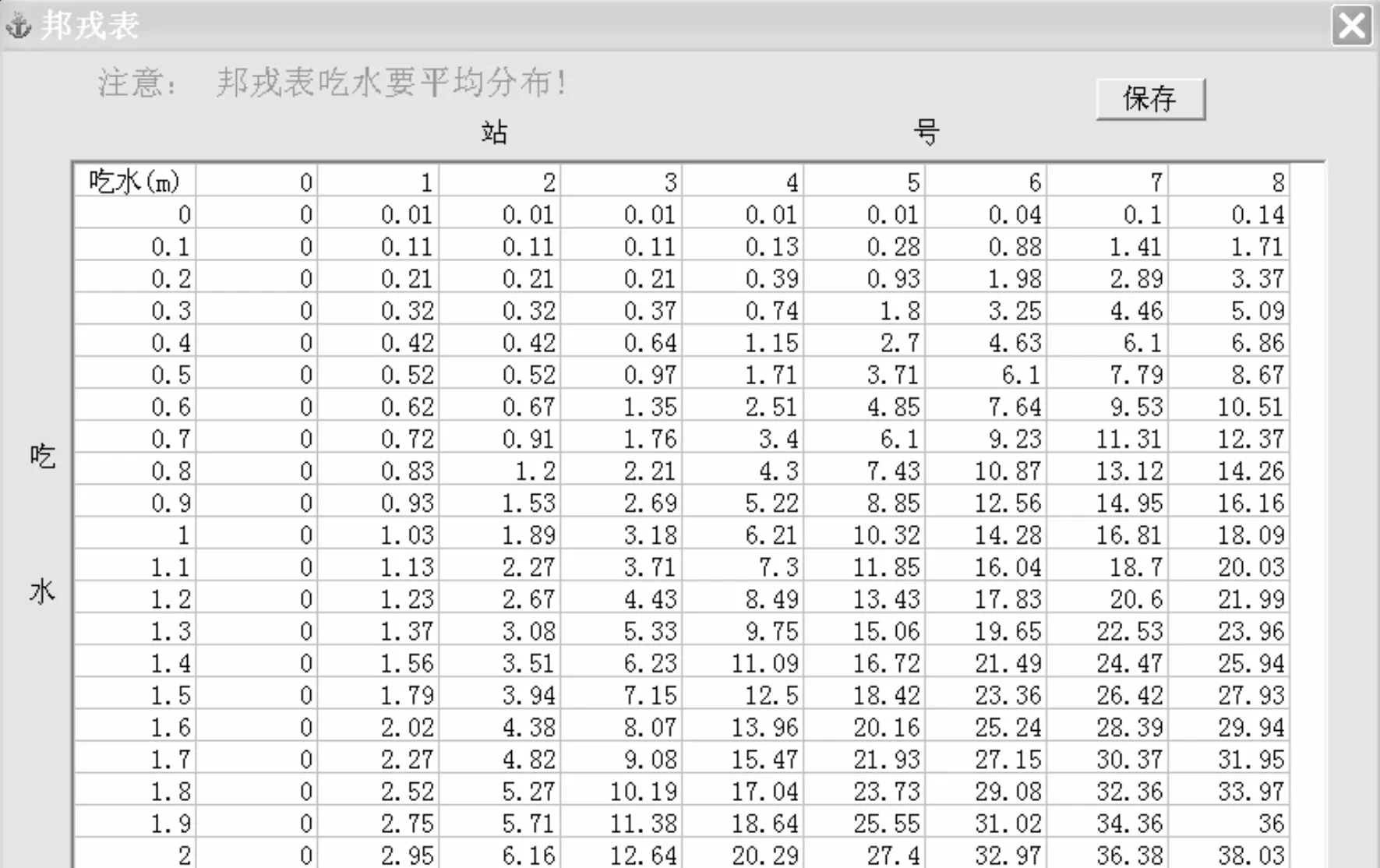
图2 邦戎表输入界面
2)使用邦戎表计算,不用考虑船型的影响。
3)采用贝塞尔曲线拟合方法计算排水量,没有站数限制,计算精度更高。
4)本程序还可以用于空船试验时的排水量估算,根据水尺读数即可计算出试验状态下的排水量,并明确显示出纵倾和中拱中垂情况。图3是本公司为PIL公司建造的27 000 DWT多用途船计算界面,和设计院的空船计算报告结果相比只差10 t左右,误差较小。

图3 空船估算界面
3 下水计算实例
2013年9月29日,本公司下水一艘海峡客滚船,是双艉船型。计算结果见图4。
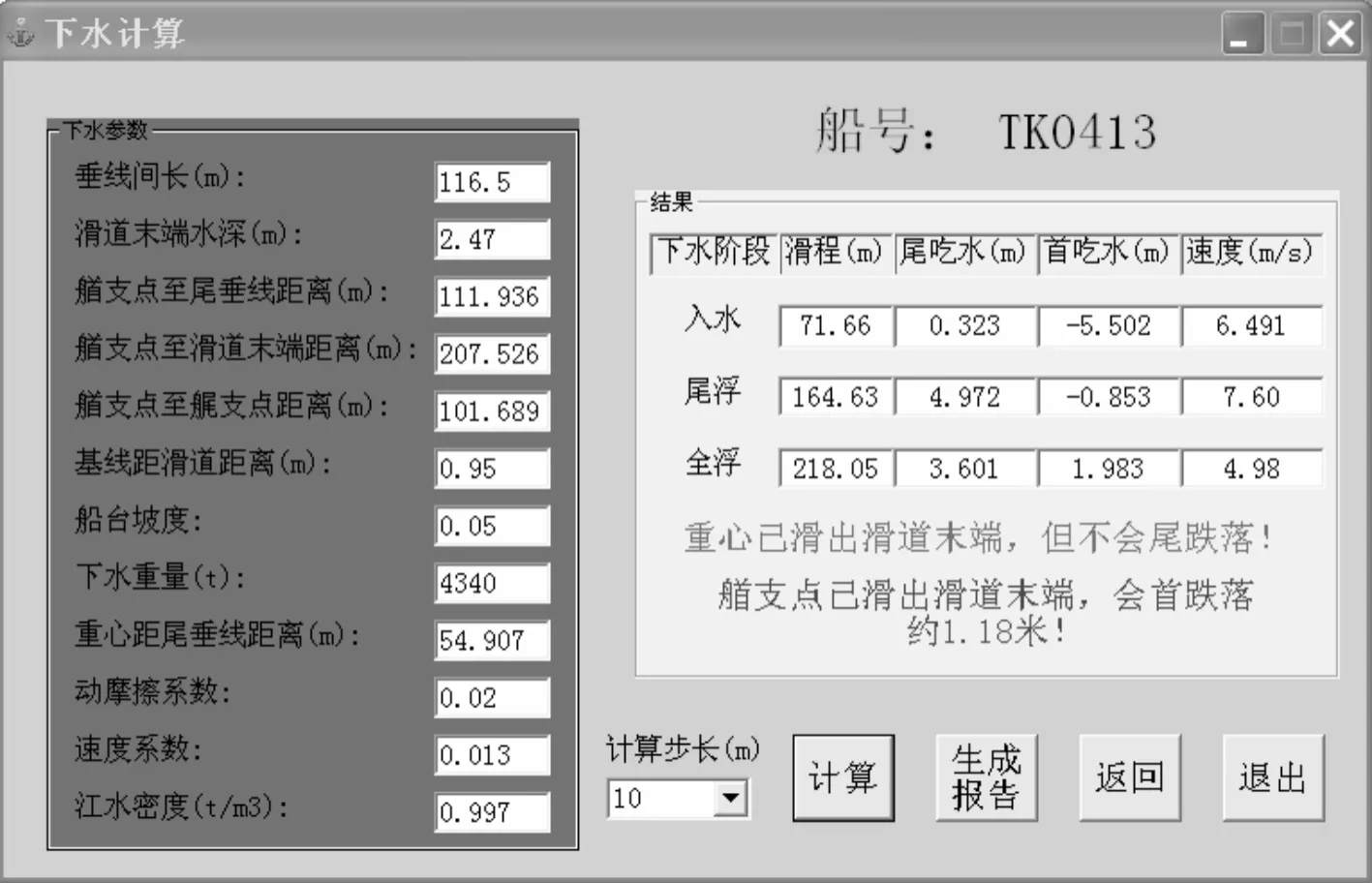
图4 下水计算界面
可以看出界面清晰显示了入水、艉浮、全浮的滑程、艏艉垂线吃水、速度等,并明确显示艉跌落、艏跌落情况。
本公司早前的51 000 DWT散货船下水时拍摄了录像,分析录像绘出了下水速度曲线,和软件生成的第二阶段速度比较见图5。可以看出软件计算和实测相差很小,证明了软件的准确性。
4 结论
本方法可缩短下水计算工作量,减少出错几率,从而提高工作效率。相比型值参数法,本方法更广泛适用于各类船型船舶的下水计算。
[1] 盛振邦,刘应中.船舶原理[M].上海:上海交通大学出版社,2003.
[2] 陈宾康.船舶静力学现代算法[M].大连:大连海事大学出版社,1995.
[3] 艾旭波.Excel VBA及贝塞尔曲线在旁压试验数据处理中的应用[J].山西建筑,2012(36):287-288.
