基于边光滑有限元法的散射声场数值计算
2014-06-27,,b,,
, ,b,,
(华中科技大学 a.船舶与海洋工程学院;b.船舶和海洋水动力湖北省重点实验室, 武汉 430074)
由于光波和无线电波在水中传播时能量衰减非常快,所以二者都不便作为水下航行体探测和导航的信息传递工具。相比之下,声波在水中具有良好的传播性能,为人类进行各种海洋活动提供了很好的平台。因此,研究水下物体的声辐射和声散射性质具有重要的现实意义。目前求解声学问题的数值方法有有限元法(FEM)、边界元法(BEM)、边界积分法、无网格技术和T矩阵法[1]等,其中FEM和BEM最为常用。FEM的缺点在于其数值离散误差会随计算频率的增加而增加,为了缩小高频段的计算误差,虽然可以细化网格,但是极大地增加了计算时间,并且没有从根本上降低误差。
为了从根本上降低FEM的数值离散误差,文献[2]结合FEM和无网格技术中的应力光滑技术提出了边光滑有限元法(ES-FEM)。该方法认为FEM数值误差的来源是模型刚度太大,而ES-FEM能通过光滑技术建立刚度更接近真实情况的模型,因此能有效减小数值离散误差。文献[3]用ES-FEM研究了固体力学中的自由振动和受迫振动问题,发现ES-FEM能得到更准确的固有频率,因此位移和应力结果也更准确。文献[4]用ES-FEM研究了声固耦合问题,发现ES-FEM能消除剪切自锁现象。
目前,国内对ES-FEM研究较少且主要集中在固体力学领域,其在声学领域的研究几乎是空白。本文采用ES-FEM计算外域声学问题,研究其在声学领域的应用价值,重点探讨其计算效率和准确性。
1 光滑有限元理论
1.1 有限元控制方程
有限元法不能直接计算无界域声学问题,需引入一个人工边界将无界域截断并在人工边界上加载一定的边界条件,以消除人工边界上的杂乱反射。那么,在声学域Ω内的控制方程有
(1)
狄利克雷边界条件p=pD
(2)
(3)
(4)
(5)
式中:ρ——流体介质密度;
vn——质点法向振动速度;
ω——角频率;
An——阻尼系数;
M——DtN算子,认为人工边界上的声压与其法向偏导数存在某种映射关系,这种关系可以用DtN算子加以描述。
对于二维问题,Givoli[5]推导并计算了当人工边界是半径为R的圆时DtN算子的表达式
(θ-ϑ)
(6)
采用Galerkin理论对式(1)进行离散化处理,并带入边界条件得外声场的总控制方程
(7)
其中刚度矩阵:
(8)
质量矩阵:
(9)
阻尼矩阵:
(10)
人工边界矩阵:
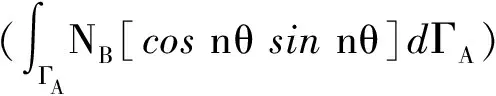
(11)
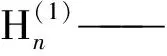
R——人工边界的半径;
NA和NB——人工边界上的任意两个节点的型函数。
力矩阵:
(12)
1.2 光滑刚度矩阵
光滑有限元法是对有限元法的一种改进,二者求解同一问题的步骤基本相同,二者的不同之处在于总刚度矩阵的建立过程不同。把式(8)中形函数的梯度项换成梯度光滑项可得光滑有限元刚度矩阵表达式为
(13)
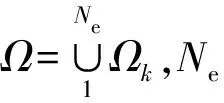
(14)
声学问题中光滑技术的本质是对质点振动速度进行光滑处理,光滑域Ωk内的速度表示为
(15)
式中:W——光滑函数,其表达式为
(16)
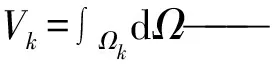
把式(16)代入式(15),并把速度在光滑域的积分变成声压在边界上的线积分
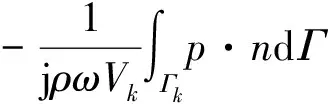
(17)
声压的光滑梯度可以简写成
(18)
式中:Nk——光滑域的节点数。
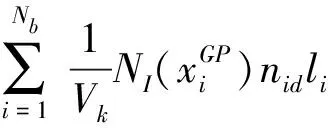
(19)
式中:bId——下标I表示节点号,d=1,2分别表示梯度沿x方向和y方向的值;
Γk——第k个光滑域的边界;
Nb——光滑边周围单元的个数,当光滑边处于边界上时取1,当光滑变处于内部时取2;
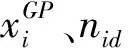
把式(18)和(19)带入式(14)得到总光滑刚度阵的表达式:
(20)
2 数值算例
2.1 ES-FEM的计算效率
FEM与ES-FEM的求解过程是一致的,二者具有相同的质量矩阵、阻尼矩阵、边界矩阵和力矩阵,二者的惟一区别在于刚度矩阵。因此比较FEM和ES-FEM的计算效率,就是比较二者单元刚度矩阵的计算时间和总刚度矩阵的装配时间。调整网格尺寸,分别采用三角形单元(T3)和四边形单元(Q4)划分计算域,各得到总节点数为576、1 196、1 620、2 176和2 660的5种模型,然后分别计算FEM和ES-FEM求解总刚度矩阵的时间,见表1。
从表1中可以观察到:随总结点数的增加,ES-FEM和FEM计算总刚度矩阵时间呈线性增加趋势;对于T3单元和Q4单元,ES-FEM计算总刚度矩阵的时间都明显少与FEM;ES-FEM计算总刚度矩阵时间受单元类型小于FEM。ES-FEM计算效率高于FEM的原因是:无论是T3单元还是Q4单元,ES-FEM将形函数梯度转换为光滑域边界积分,继而用高斯公式将积分运算变为加法运算,因此ES-FEM无需进行数值微分运算;根据式(19)得到的光滑梯度是常数值,因而ES-FEM也无需进行数值积分运算。
2.2 ES-FEM计算的准确性
以无界域中二维舵的对平面波散射场计算为例,分析ES-FEM计算结果的准确性。设平面波沿x轴正向传播,其表达式为
p=exp(-jkx)
(21)
计算域是由舵的外轮廓和人工边界所围成的区域,用T3单元划分网格,调整网格尺寸得到34 285节点的精细网格和3 783节点的粗糙网格。由于舵表面曲率复杂不能推导解析解,把精细网格下的FEM计算结果作为参考解,见图1a)、2a)。分别用FEM和ES-FEM计算波数k=3π(低频)和波数k=15π(高频)时的散射声场,结果见图1和图2。

图1 波数k=3π时的散射声场
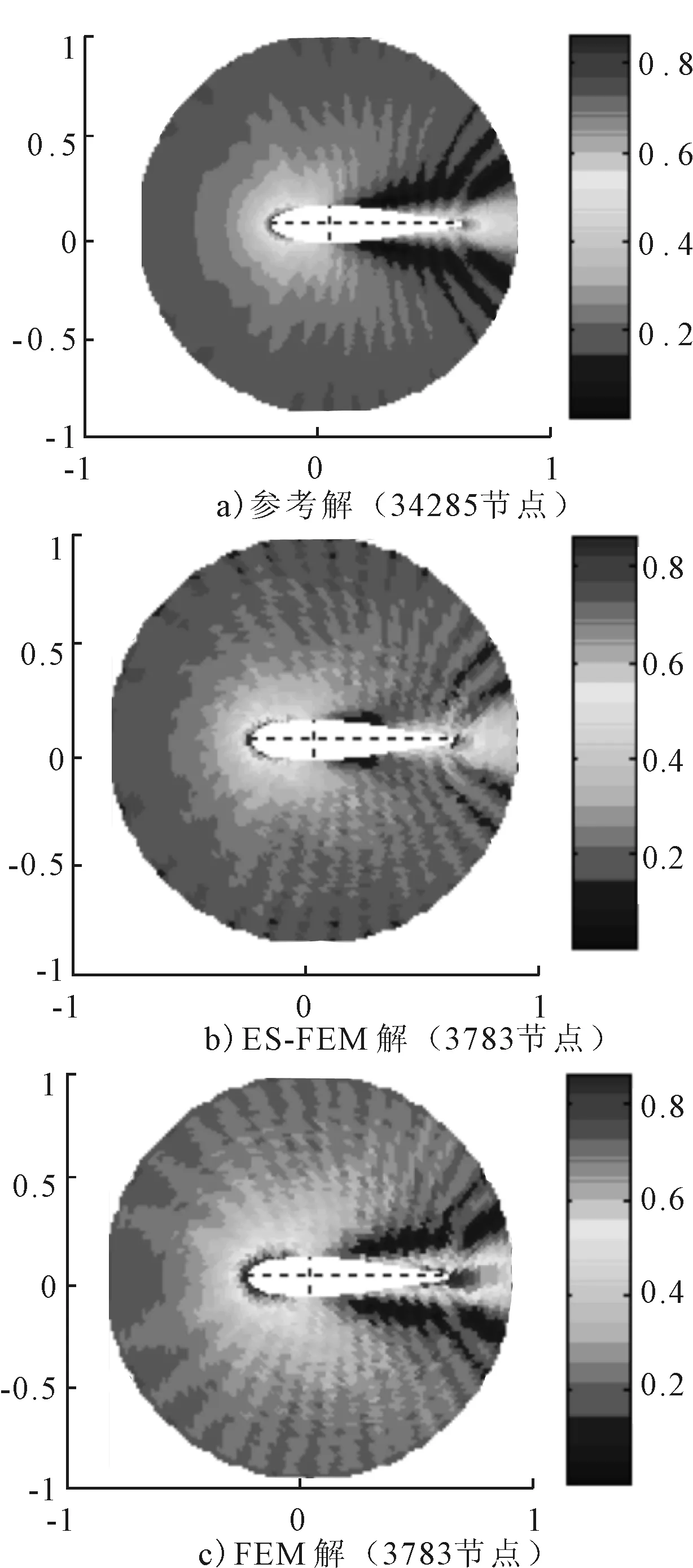
图2 波数k=15π时的散射声场
由图1可见,当入射波频率较低时,粗糙网格下FEM和ES-FEM计算结果均与精细网格下FEM计算结果十分吻合;而由图2中可以看出,当入射波频率较高时,ES-FEM解的云图中干涉条纹和舵首尾处的散射场仍比较接近参考解,而同网格质量下FEM解的云图中干涉条纹不清晰,舵首尾处的散射场与参考解相差较大。
图3是人工边界上反向散射点的散射声压值随入射波波数的变化曲线,图中曲线是振荡变化的。根据文献[1]的解释,对于刚性体的散射,这种振荡现象是由于镜反射波和绕射波发生干涉引起的。从图中可以看到,当入射波波数较小时,ES-FEM解和FEM解十分接近,并且二者曲线仅在波峰波谷位置与参考解有差异。当入射波波数较大时,ES-FEM解与FEM解都和参考解有较大差异,但是ES-FEM解中波峰波谷处所对应的波数值比FEM解更加接近参考解,就这一方面而言,ES-FEM解比FEM解更准确。
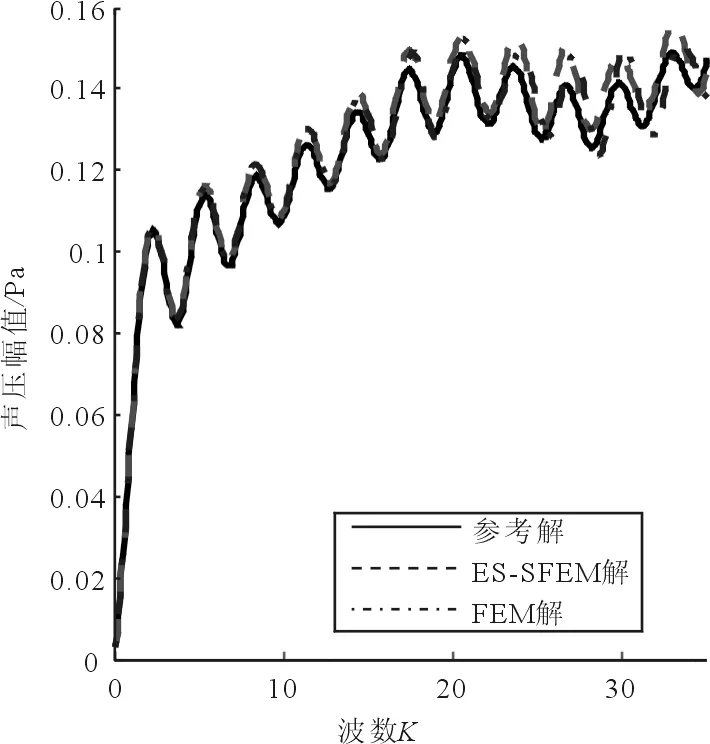
图3 反向散射声压随波数变化曲线
3 结论
1)ES-FEM用光滑技术把形函数梯度的域积分变为域边界的线积分,减少了FEM数值积分和数值微分的计算时间,极大地提高了计算效率。
2)用ES-FEM计算无界域中二维舵对平面波的散射声场,并与精细网格下FEM的计算结果进行比较,发现ES-FEM在低频段的计算结果十分准确,而在高频段的计算结果比同网格质量下FEM的计算结果更准确。
3)水下声学是海洋工程的重要分支,目前对于大型水下航行体如潜艇的回波特性分析需借助工程软件,ES-FEM对于优化基于FEM理论的声学工程软件提供了新的思路。
[1] 李 威,赵 耀,张 涛,等.水下刚硬体声散射场计算及分析[J].声学技术,2007,26(5):844-849.
[2] LIU G R, NGUYEN T T,LAM K Y.An edge-based smoothed finite element method (ES-FEM) for static free, and forced vibration analysis [J]. Journal of Sound and Vibration,2009,320:1100-1130.
[3] DAI K Y,LIU G R.Free and forced vibration analysis using the smoothed finite element method (SFEM) [J]. Journal of Sound and Vibration,2007,301:803-820.
[4] HE Z C,LIU G R,ZHONG Z H,et al.Coupled analysis of 3D structural-acoustic problems using the edge-based smoothed finite element method/finite element method [J]. Finite Elements in Analysis and Design,2010,46:1114-1121.
[5] KELLER B,GIVOLI D.Exact non-reflecting boundary conditions [J]. Journal of Computational. Physics,1988,82:172-192.
