基于改进的粒子群优化扩展卡尔曼滤波算法的锂电池模型参数辨识与荷电状态估计

项宇,马晓军,刘春光,可荣硕,赵梓旭

（装甲兵工程学院控制工程系,北京 100072）

基于改进的粒子群优化扩展卡尔曼滤波算法的锂电池模型参数辨识与荷电状态估计

项宇,马晓军,刘春光,可荣硕,赵梓旭

（装甲兵工程学院控制工程系,北京 100072）

为解决锂电池荷电状态（SOC）难以精确估计的问题,提出了基于改进的粒子群优化扩展卡尔曼滤波（IPSO-EKF）算法预测电池SOC。为减小参数非线性特性影响,重新构建了EKF算法电池状态空间方程,以辨识出的电池模型参数为基础,获得SOC最优估计。采用IPSO算法优化EKF算法噪声方差矩阵,解决系统状态误差协方差矩阵和测量噪声协方差矩阵最优解获取难题,进一步提高SOC的估计精度。计算结果表明：IPSO-EKF算法能够精确地辨识电池模型参数和SOC值,并能够很好地修正状态变量初始误差。

电气工程；锂电池；荷电状态；模型参数；粒子群优化算法；扩展卡尔曼滤波

0 引言

为满足未来陆战平台发展需求,以动力电池为辅助动力的混合动力系统成为电传动装甲车辆首选方案[1]。准确而实时地获取电池的荷电状态（SOC）信息是混合动力系统功率分配控制研究的关键技术,由此衍生的电池SOC估计成为近年来研究的热点。

目前电池SOC预测方法较多。积分法及其改进方法最为简单[2],在工程实践中多采用此种方法,但是存在误差积累,且不能修正初始误差,精度较低。文献[3]中介绍的开路电压法,只能在静态条件下通过开路电压与SOC关系精确辨识SOC值,不适用于动态过程。文献[4]采用的内阻法,依赖电池内阻的精确测量,应用条件苛刻,实际应用较为困难。文献[5]中的线性模型法,适用于不同类型和老化阶段的电池,但不适合本文研究对象工作在大电流以及电流剧烈变化的情况。文献[6]中的神经网络法虽能够很好地解决SOC预测这一非线性过程,但是其精度依赖大量的训练样本和训练方法。

美国Colorado大学的Plett首次将卡尔曼滤波（KF）方法应用于锂电池管理系统中[7-11],研究了扩展卡尔曼滤波（EKF）、SP-KF、SR-SPKF算法及其联合算法在锂离子电池SOC估计、参数辨识、健康状态估计、输出能力计算以及电压平衡等方面的应用,极大地提高了锂电池优化控制与管理水平。国内的学者也对KF算法在电池管理系统中的应用进行了研究,文献[12]介绍了采用适用于非线性状态估计的EKF算法[13]预测电池SOC,也取得了很好的效果。但是在他们的研究中仍然存在不足之处,他们都在状态方程线性化过程中忽略了高阶项,降低了模型精度。后者在算法中使用的电池内阻等时变参数以常数代替,引入了参数误差,前者虽然考虑了模型参数的时变特性,但为了降低状态方程的阶数,仅考虑了锂电池的电化学极化特性,而没有考虑浓度差极化对电池输出特性的影响。SOC预测效果严重依赖噪声统计特性,而系统噪声和测量噪声的统计特性很难获得最优解。

本文以某型锂电池单体为研究对象,在对前述文献中用EKF算法预测电池SOC过程中存在的不足进行深入研究的基础上,提出了改进的粒子群优化扩展卡尔曼滤波（IPSO-EKF）算法,在系统状态变量中引入表征电池电化学极化和浓度差极化特性的电池二阶RC模型参数,进行实时的电池参数辨识和SOC估计。计算结果表明,该算法能够准确地辨识锂电池内部参数,以此为基础的电池SOC预测精度较高,并具有良好的初始误差适应性。

1 电池模型

本文提出的参数辨识和SOC预测算法基于如图1所示的锂电池2阶RC模型。

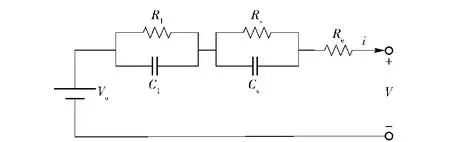
图1 锂电池2阶RC模型Fig.1 Second-order resistance-capacitance network model of lithium battery

图1中：Vo为开路电压；V为端电压；i为电流； Re为欧姆内阻；Rs、Cs用于模拟电化学极化反应,Rs为电化学极化电阻,Cs为电化学极化电容；Rl、Cl用于模拟浓度差极化反应,Rl为浓度差极化电阻,Cl为浓度差极化电容。

以电池SOC、两电容上的电压Vs、Vl作为状态变量,电池状态方程为

为静态时电池端电压与SOC值之间的关系函数。

2 扩展卡尔曼滤波器设计

2.1 非线性滤波方程及其线性化处理

仅根据（1）式和（2）式应用KF算法进行SOC估计时,方程中的模型参数是定值。为提高滤波算法对参数时变的适应性,在电池状态空间方程中引入模型参数进行实时辨识。假设在采样周期T内电流与开路电压的变化忽略不计,（2）式两侧求导可得

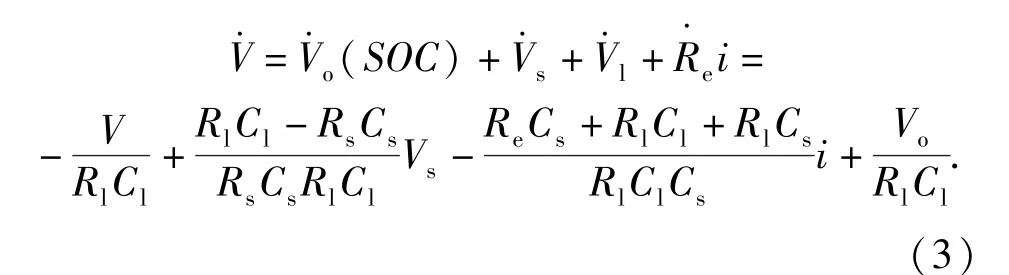
将模型的参数也作为状态变量,结合（1）式和（3）式可构建基于EKF算法的锂电池模型参数辨识和SOC估算状态方程,对其进行离散化处理后如（4）式所示。

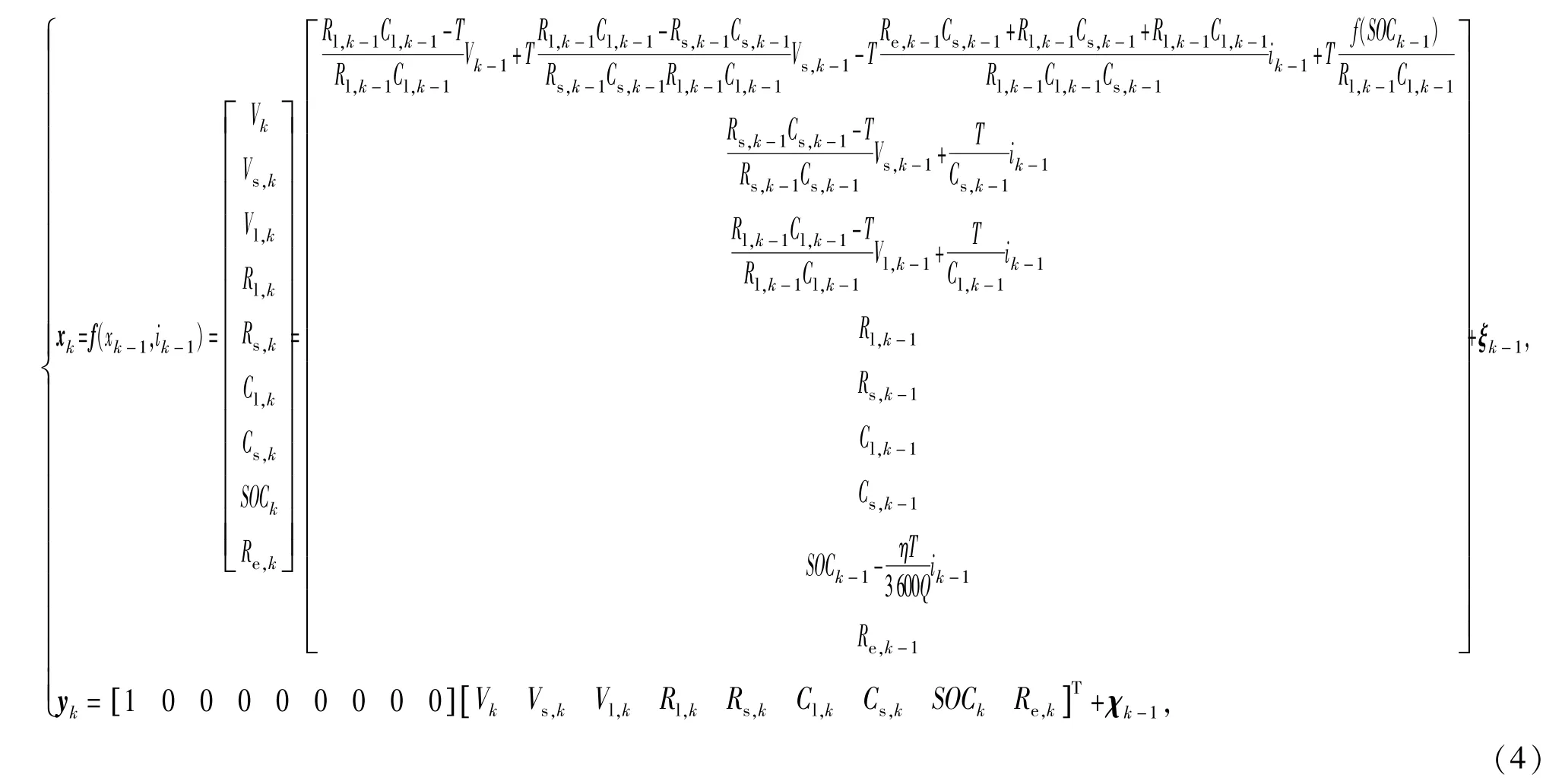
式中：ξk为随机干扰；χk为随机观测噪声。

由（4）式知,电池状态方程为非线性方程,测量方程为线性方程,使用EKF算法进行参数辨识和SOC估计时,需对滤波方程进行线性化处理[14]。其思想是：在状态估计时,对状态方程f（xk,ik）在前一状态估计值xk+1|k处做实时的泰勒近似,略去2阶以上高阶项。

经线性化处理后得到的离散非线性滤波方程为

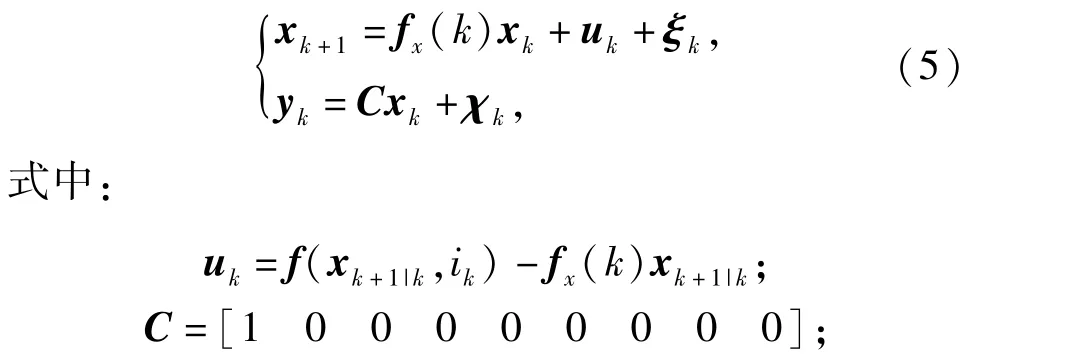
2.2 EKF算法递推流程

滤波过程稳定,是应用KF算法的前提,根据分段定常系统理论（PWCS）[15]可证明本文研究的系统状态变量一致完全可观、一致完全可控,滤波过程稳定。可用EKF算法进行模型参数辨识和SOC估计。

若已知系统随机干扰ξk、随机观测噪声χk和状态变量初始值x0的统计特性如下：

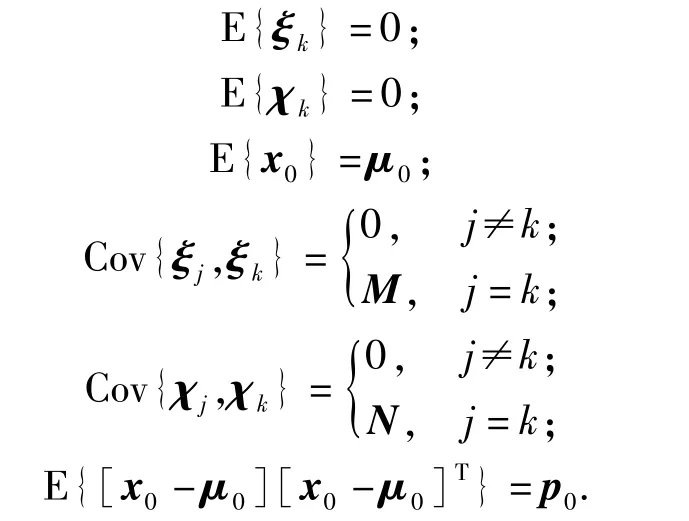
式中：M、N分别为状态变量和端电压测量值的协方差矩阵。

以状态变量初始值x0=μ0,估计误差方差矩阵初始值P0=p0,作为k=0时EKF算法初始值启动递推算法。当k=1,2,3,…时,算法递推过程如下：

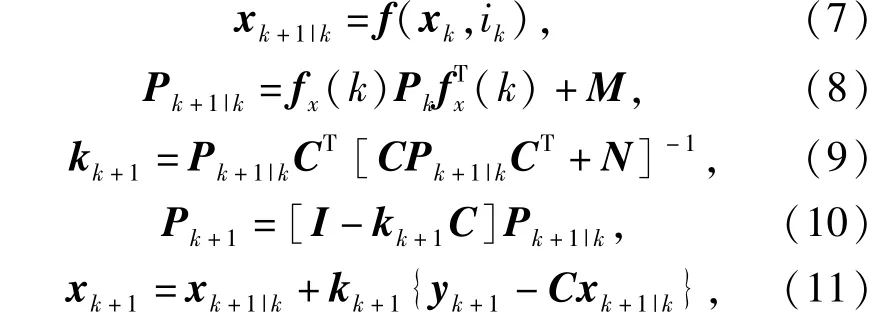
式中：yk+1为第k+1次采样获得的端电压Vk；I为单位矩阵；xk+1|k为状态变量预测矩阵；xk+1为更新的状态变量输出矩阵；Pk+1|k为误差协方差预测矩阵； Pk+1为更新的误差协方差矩阵；kk+1为更新的滤波增益状态矩阵。

根据EKF递推公式和电池空间状态方程,滤波器观测步骤如下：

1）预测更新。根据电流ik和前一次估计值xk,代入式f（xk,ik）对状态变量进行一步预测得xk+1|k,并计算对应的输出预测yk+1=Cxk+1|k.并根据（6）式和（8）式对误差协方差矩阵Pk+1|k进行预测。

2）增益矩阵和测量更新。根据预测得到的误差协方差矩阵Pk+1|k和（9）式得到滤波增益kk+1.根据预测值对状态变量进行反馈校正,由（10）式计算误差协方差矩阵最优估计Pk+1,由（11）式计算状态最优估计xk+1.

由前述可知,包括电池模型参数和SOC在内的状态最优估计xk+1能被递推求出。在进行SOC预测时,以实时辨识的电池内部参数为基础,通过安时法计算电池SOC值,与开路电压法结合计算开路电压,同时估算电池内部压降,将算得的电池端电压值与实测值比较,校正SOC预测值SOCk+1.实现了安时积分法、开路电压法、EKF算法的联合和SOC值的实时闭环估计。

2.3 参数辨识的准确性探讨

电池SOC估计的准确性和收敛性依赖电池模型参数的准确辨识,在此对本文采用的KF算法中参数辨识的准确性进行分析。在文献[9]和文献[12]中,都提出并采用了双KF的方法同时实现电池模型参数的辨识和SOC的估计,其算法框图如图2所示。

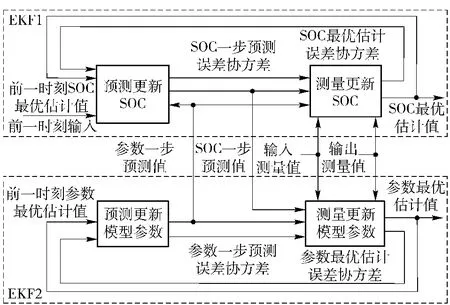
图2 基于双EKF的电池参数辨识和SOC估计Fig.2 Block diagram of battery parameters and SOC estimation algorithm based on dual EKF

其主要思想是交替使用模型参数来估计SOC和使用SOC来进行模型参数辨识。图2中,EKF1算法实现对电池SOC的估计,除系统输入输出外,还依赖于电池模型参数的一步预测值；而在电池模型参数辨识的EKF2算法则依赖SOC的一步预测值。由于电池模型参数变化缓慢,在算法周期内作为恒定值处理,在文献[9]和本文（7）式中均把模型参数前一时刻最优估计值作为当前时刻一步预测值。

对比可知,双EKF算法与本文采用的EKF算法是完全等效的,二者的区别是：需要辨识的模型参数的数量不同；与本文滤波算法相比使用双EKF算法能够降低状态方程的维数,使得方程的运算速度更高效,但是其算法结构相对较为复杂。因此,基于文献[9]中的研究成果可知,本文提出的滤波算法完全能够保证电池模型参数辨识的准确性,以此为基础的SOC估计是可靠的。

3 IPSO-EKF算法

为获得精确的噪声协方差矩阵M和N,进一步提高参数辨识和SOC估计效果,有学者将智能优化算法应用于参数优化。文献[16]中采用遗传算法优化噪声方差矩阵,取得一定效果,但是遗传算法操作复杂,优化效率低。在此,本文采用宏观搜索能力和鲁棒性较强的IPSO算法获取噪声协方差最优解。

3.1 IPSO算法

粒子群优化（PSO）算法是一种生物进化算法[17],种群中的每个粒子都代表问题的一个潜在解,对应一个由适应度函数决定的适应度值。粒子的速度决定了粒子移动的方向和距离,速度随自身及其他粒子的移动经验进行动态调整,实现个体在可解空间中的寻优。

设在D维的目标搜索空间中,由F个粒子组成一个种群,第f个粒子的位置用xf,d=[xf,1,xf,2,…, xf,D]表示,飞行速度用vf,d=[vf,1,vf,2,…,vf,D]表示,第f个粒子搜索到的最优位置为pf,d=[pf,1,pf,2,…, pf,D],粒子群搜索到的最优位置表示为gf,d=[gf,1, gf,2,…,gf,D],标准PSO中粒子速度和位置更新过程为

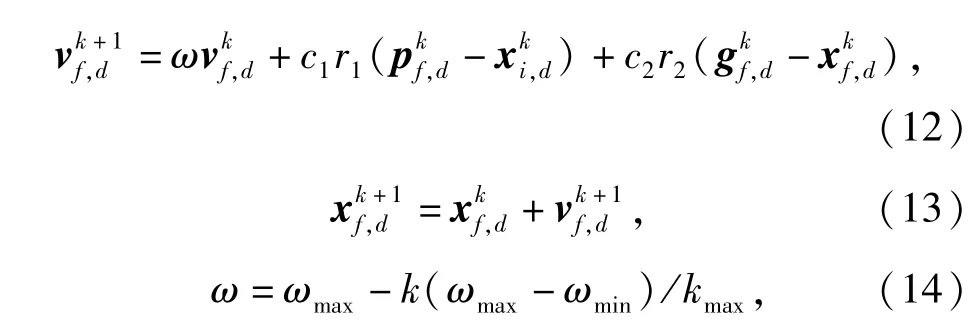
式中：f=1,2,…F；d=1,2,…D；c1、c2为学习因子； r1、r2为[0,1]之间的随机数；xf,d∈[-Xmax,Xmax]、vf,d∈[-Vmax,Vmax]；ω、ωmax、ωmin分别为惯性权重、最大权重、最小权重；k、kmax分别为迭代次数和最大迭代次数。当ωmax=0.9,ωmin=0.4时,迭代初期ω较大,算法具有较强的全局搜索能力,迭代后期ω较小则算法倾向于更精确的局部搜索。

为克服标准PSO算法在应用中存在的遍历性差和容易陷入极小的缺点,对算法过程作了如下改进：

改进一,为提高种群的多样性和粒子搜索的遍历性。采用具有较强寻优能力的分段Logistic混沌映射初始化粒子群的速度和位置[18],表达式为

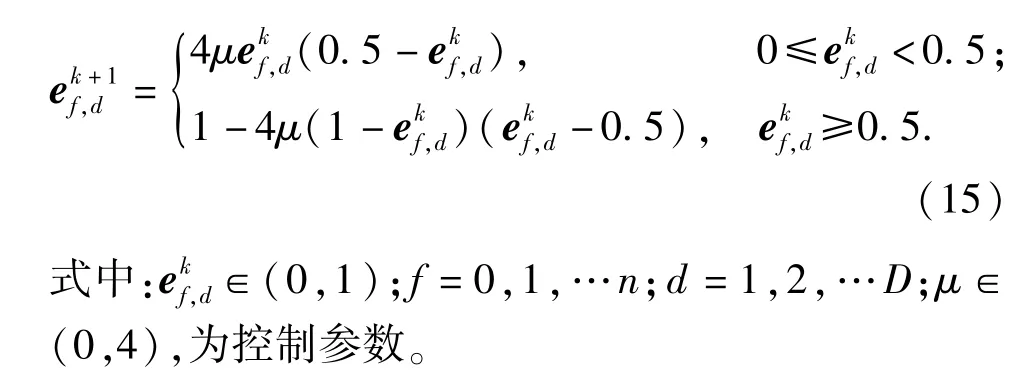
粒子群位置和速度的混沌初始化过程为：

1）随机产F×D维矩阵E=ef,d,e1,d,通过（15）式进行迭代,用第k次迭代的结果更新ek,d,直至k=F.

2）最后通过（16）式将ef,d映射到粒子f第d维位置的混沌搜索区域（-rf,d,rf,d）内,可得初始化的粒子速度和位置

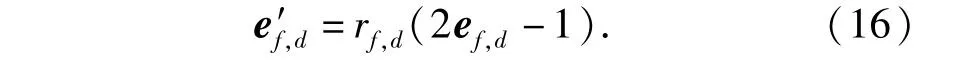
3.2 IPSO优化EKF噪声方差矩阵

IPSO优化目标是噪声方差矩阵M和N,共10个参数,即D=10.随机产生的F×D维种群粒子位置和速度初始矩阵经（15）式和（16）式进行混沌映射初始化,再由（12）式～（14）式进行粒子和速度更新。

粒子最优位置的选择由粒子适应度函数决定,即每一组赋值的噪声方差矩阵应用于EKF算法估算电池SOC的效果。在此选用测量方程的预测值Cxk+1|k与测量值yk+1的绝对误差累计作为粒子适应度值fitness,如（17）式所示。

式中：L表示离散频率点的最大采样点数。

最终,IPSO-EKF算法进行电池参数辨识和SOC预测算法流程如图3所示。

本文研究的锂电池单体参数为：额定容量50 A·h,额定电压4.2 V,最小电压3 V.采用IPSO算法优化EKF噪声方差时,IPSO算法参数设置为：种群规模F=30,迭代次数为20,学习因子c1=c2= 1,最大惯性权值ωmax=0.9,最小惯性权值ωmin= 0.4,控制系数μ=4,粒子聚集度判定值ε=0.01,混沌搜索半径rfd=1.

由于电池的状态变量与电池充放电电流和SOC有关,不同的电流和SOC时的噪声方差也有所不同。当电池以0.2 C放电,电池SOC为90%时,运行IPSO算法得到如图4所示的粒子群平均适应度值和全局最佳适应度值变化曲线。由图4可知,经8次迭代后全局最佳适应度值趋向稳定；随着迭代次数的增加,平均适应度迅速减小,并趋向稳定,说明此时得到的粒子种群值为最优解。

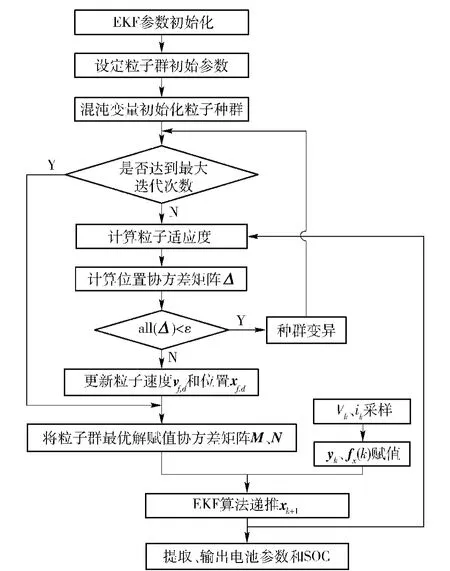
图3 IPSO优化EKF算法流程Fig.3 The flow chart of EKF algorithm optimized by IPSO

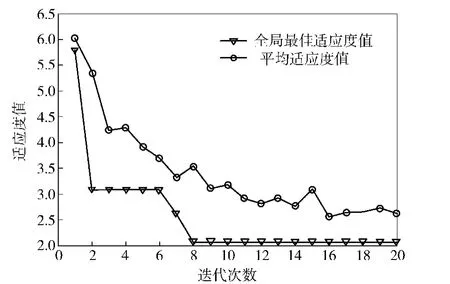
图4 IPSO算法过程中适应度值变化曲线Fig.4 The adaptive value curves calculated by IPSO algorithm

4 算法辨识与估计结果

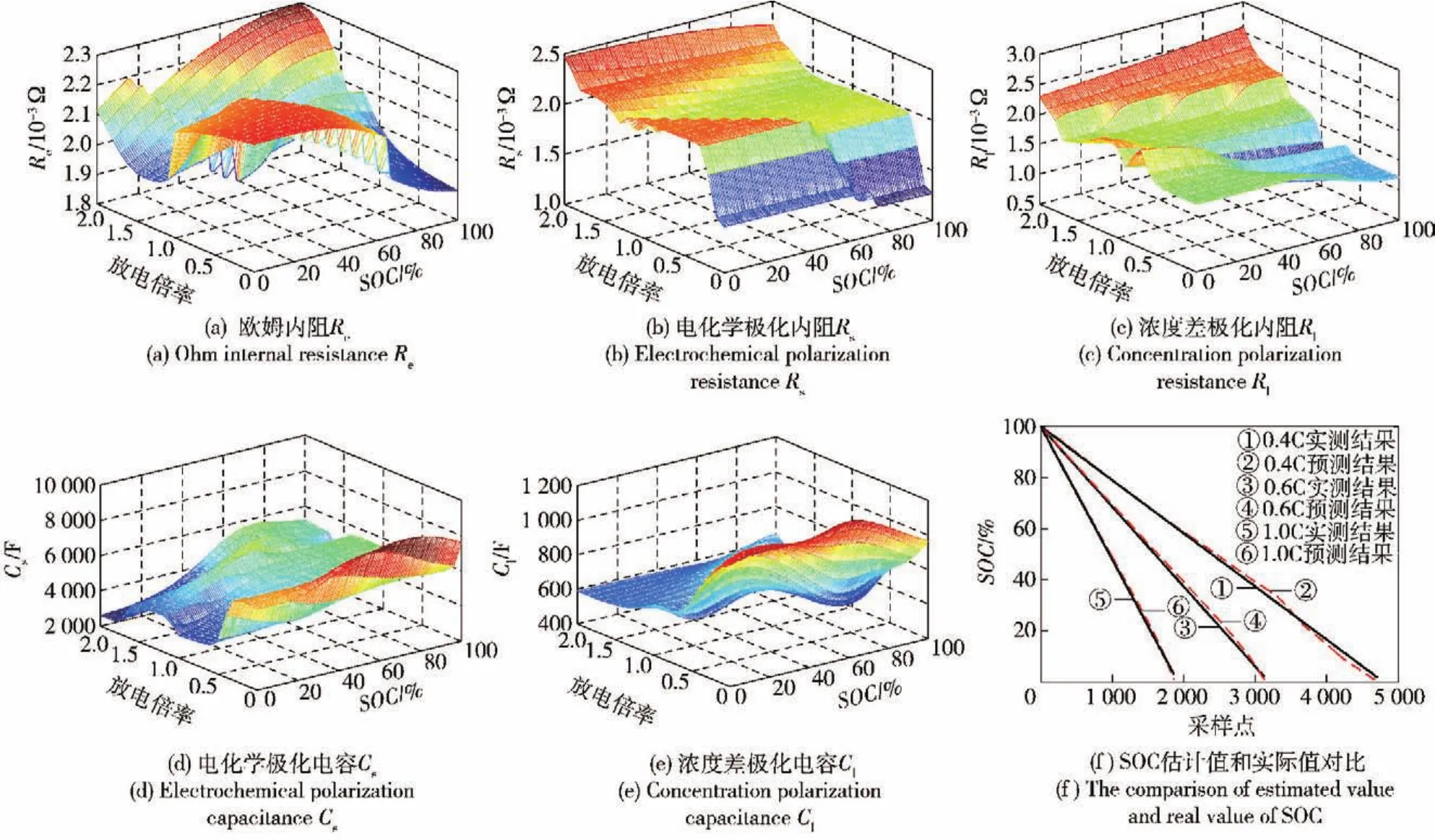
图5 参数辨识与SOC估计结果Fig.5 Parameter identification and estimated results of SOC

利用IPSO-EKF算法辨识锂电池参数并进行SOC估计。当锂电池在满电荷状态下,分别以0.2 C、0.4 C、0.6 C、0.8 C、1.0 C、1.2 C、1.4 C、1.6 C、1.8 C、2.0 C恒流放电,辨识结果如图5所示。

由图5（a）、图5（b）、图5（c）可知,放电电流恒定时,欧姆内阻Re、电化学极化内阻Rs和浓度差极化内阻Rl随SOC的降低而增大；SOC恒定时,Re、Rs和Rl随放电电流的增大而增大。如图5（d）、图5（e）所示,电池电化学极化电容Cs、浓度差极化电容Cl的变化趋势与相应的极化内阻Rs、Rl的变化趋势相反,由于模型中对应的极化内阻和极化电容并联,因此,当电池放电电流增大和SOC降低时,电池的极化压降都会增大。内阻和电容的变化规律都符合电池的实际工作特性。

对相同的放电过程,电池每放电一段时间对其进行搁置,应用开路电压法精确测得电池剩余电量,与IPSO-EKF算法估计的SOC值进行比较,如图5（f）所示。由图5（f）可知,不同充放电条件下基于IPSO-EKF算法的SOC估计值和实测值较为接近,绝对估计误差均在2%以内,因此基于IPSO-EKF算法能够准确有效地估计电池的SOC值。

图6（a）为锂电池单体端电压和电流变化曲线,图6（b）为在车辆行驶工况中不同估计算法估算的锂电池SOC曲线。由图6可知,与定参数EKF算法相比,具有参数估计的EKF算法和IPSO-EKF算法估计SOC值更接近开路电压法SOC估计值。相对于能够实时辨识参数的EKF算法,定参数EKF算法估计误差较大的原因主要是由于电池电流和SOC的变化引起电池模型参数变化,基于定参数的EKF算法适应性降低,误差增大。而基于实时电池模型参数辨识的EKF算法适应性较好,估计精度也有很大提高。而采用IPSO算法优化模型参数辨识的EKF算法中的噪声方差矩阵,使得基于模型参数辨识的EKF算法的估计精度进一步得到提升。表明IPSO-EKF算法有效地降低了电池模型参数时变和噪声方差统计特性不确定性对SOC估计的影响。

为检验IPSO-EKF算法对SOC初始误差的修正能力,在电池实际初始SOC为80%、以0.5C电流放电时,采用IPSO-EKF算法估计SOC.当状态变量x0中SOC初始值分别为10%、30%、50%、70%和90%时,前200 s的SOC估计曲线如图7所示。由图7可知,不同初始误差情况下的SOC估计曲线均能很快收敛一致。虽然随着初始误差的增加,SOC估计曲线的收敛时间变长,但是能够确保在180 s内收敛到理想值,说明IPSO-EKF算法对SOC的初始误差具有很强的修正能力,克服了安时法不能消除初始误差的缺点。

5 结论

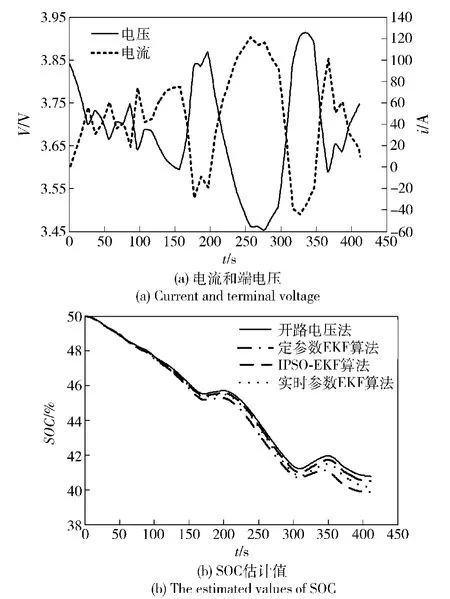
图6 车辆行驶工况中电池电流、电压及SOC估计值Fig.6 Batteries'current,voltage and SOC when the Vehicle was driving

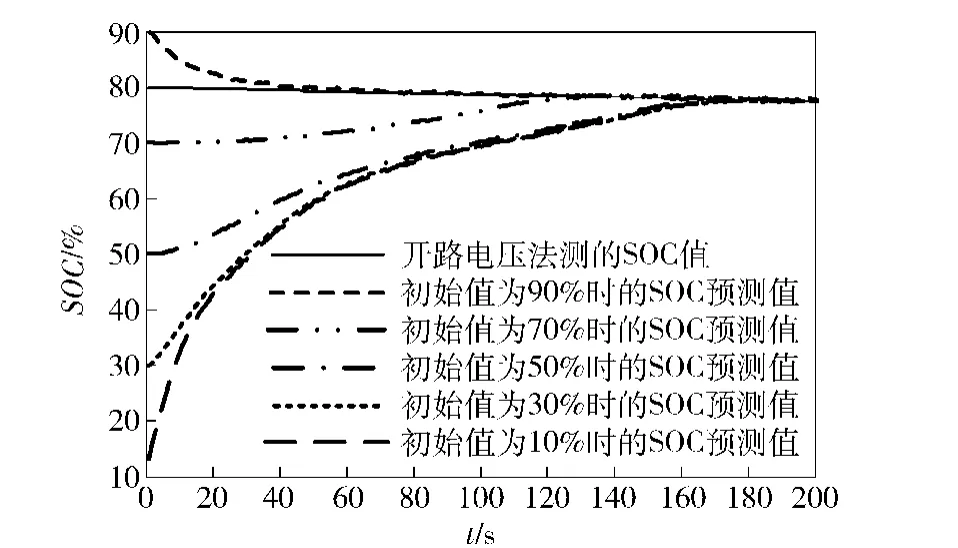
图7 电池放电过程SOC估计曲线Fig.7 The estimated curves of SOC in the process of battery discharge

为了提高电传动装甲车辆用锂离子动力电池SOC值估计精度,本文提出了一种能够精确辨识电池模型参数和估计SOC值的IPSO-EFK滤波方法。计算结果表明,与定参数EKF滤波算法和实时参数辨识的EKF滤波算法相比,IPSO-EKF算法SOC估计精度更高,算法收敛后,绝对估计误差在2%以内,并具有较强的初始误差修正能力。本文研究成果为锂电池SOC估计提供了一种新的方法,对基于精确SOC值的电传动装甲车辆能量管理控制策略研究具有重要意义。由于本文提出的SOC估计算法较为复杂,下一步工作着重于在保证SOC估计精度的前提下对算法进行优化处理,保证算法的实时性。

（References）

[1] 孙逢春,张承宁.装甲车辆混合动力电传动技术[M].北京：国防工业出版社,2008.

SUN Feng-chun,ZHANG Cheng-ning.Technologies for the hybrid electric drive system of armored vehicle[M].Beijing：National Defense Industry Press,2008.（in Chinese）

[2] 李哲,卢兰光,欧阳明高.提高安时积分法估算电池SOC精度的方法比较[J].清华大学学报：自然科学版,2011,50（8）： 1293-1296.

LI Zhe,LU Lan-guang,OUYANG Ming-gao.Comparison of methods for improving SOC estimation accuracy through an ampere-hour integration approach[J].Journal of Tsinghua University：Science and Technology Edition,2011,50（8）：1293-1296.（in Chinese）

[3] 曾洁,卜凡涛.基于多项式回归算法的锂电池SOC估测[J].大连交通大学学报,2011,32（4）：70-74.

ZENG Jie,BU Fan-tao.Study of SOC estimation and measurement of Li-ion battery based on polynomial regression algorithm[J]. Journal of Dalian Jiaotong University,2011,32（4）：70-74.（in Chinese）

[4] 林成涛,王军平,陈全世.电动汽车SOC估计方法原理与应用[J].电池,2004,34（5）：336-338.

LIN Cheng-tao,WANG Jun-ping,CHEN Quan-shi.Methods for state of charge estimation of EV batteries and their application[J]. Battery Bimonthly,2004,34（5）：336-338.（in Chinese）

[5] 李超.电动汽车用镍氢电池模型参数辨识和SOC估算研究[D].天津：天津大学,2007.

LI Chao.Study on parameter identification and SOC estimation of Ni/MH battery for EV[D].Tianjin：Tianjin University,2007. （in Chinese）

[6] 雷肖,陈清泉,刘开培,等.电动车蓄电池荷电状态估计的神经网络方法[J].电工技术学报,2007,22（8）：155-160.

LEI Xiao,CHEN Qing-quan,LIU Kai-pei,et al.Battery state of charge estimation based on neural-network for electric vehicles[J]. Transactions of China Electrotechnical Society,2007,22（8）： 155-160.（in Chinese）

[7] Plett G L.Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs：part 1.background[J]. Journal of Power Sources,2004,134（2）：252-261.

[8] Plett G L.Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs：part 2.Moding and identification[J].Journal of Power Sources,2004,134（2）：262-276.

[9] Plett G L.Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs：part 3.state and parameter estimation[J].Journal of Power Sources,2004,134（2）：277-292.

[10] Plett G L.Sigma-point Kalman filtering for battery management systems of LiPB-based HEV battery packs：part 1：introduction and state estimation[J].Journal of Power Sources,2006,161（7）： 1356-1368.

[11] Plett G L.Sigma-point Kalman filtering for battery management systems of LiPB-based HEV battery packs：part 2.simultaneous state and parameter estimation[J].Journal of Power Sources, 2006,161（7）：1369-1384.

[12] 戴海峰,魏学哲,孙泽昌.基于扩展卡尔曼滤波算法的燃料电池车用锂离子动力电池荷电状态估计[J].机械工程学报, 2007,43（2）：92-95.

DAI Hai-feng,WEI Xue-zhe,SUN Ze-chang.Estimate state of charge of power lithium-ion batteries used on fuel cell hybrid vehicle with method based on extended Kalman filtering[J].Chinese Journal of Mechanical Engineering,2007,43（2）：92-95. （in Chinese）

[13] ZONG C F,SONG P,HU D.Reduced-order EKF application in a marine INS/GPS navigation system[J].Journal of Zhejiang University-Science A：Applied Physics and Engineering Edition, 2011,12（6）：446-452.

[14] Chui C K,Chen G R.Kalman filtering with real-time applications[M]. Berlin：Springer Press,2009.

[15] Goshen-Meskin D,Bar-Itzhack I Y.Observability analysis of piece-wise constant systems-II：application to inertial navigation in-flight alignment[J].IEEE Transactions on Aerospace and Electronic Systems,1992,28（4）：1068-1075.

[16] 张彩萍,姜久春.用基于遗传优化的扩展卡尔曼滤波算法辨识电池模型参数[J].吉林大学学报：工学版,2012,42（3）： 732-737.

ZHANG Cai-ping,JIANG Jiu-chun.Extended Kalman filter algorithm for parameters identification of dynamic battery model based on genetic algorithm optimization[J].Journal of Jilin University：Engineering and Technology Edition,2012,42（3）：732-737.（in Chinese）

[17] Kenedy J,Eberhart R C.Particle swarm optimization[C]∥Proceedings of International Conference on Neural Networks.New York：IEEE,1995：1942-1948.

[18] 余爱华.Logistic模型的研究[D].南京：南京林业大学, 2003.

YU Ai-hua.A study on Logistic model[D].Nanjing：Nanjing Forestry University,2003.（in Chinese）

Estimation of Model Parameters and SOC of Lithium Batteries Based on IPSO-EKF

XIANG Yu,MA Xiao-jun,LIU Chun-guang,KE Rong-shuo,ZHAO Zi-xu
（Department of Control Engineering,Academy of Armored Force Engineering,Beijing 100072,China）

An extended Kalman filter（EKF）which is optimized by the improved particle swarm optimization（IPSO）algorithm is proposed to estimate the state-of-charge（SOC）of battery.A new state space equation applied to EKF algorithm is constituted to reduce the influence of non-linear characteristics of parameters,and the optimal estimation of SOC is obtained based on the real-time identification of battery model parameters.IPSO algorithm is applied to optimize the system state error covariance matrix and measurement noise covariance matrix to improve the estimation accuracy of SOC by solving the problems in achieving the optimal solutions of these covariance matrixes.The results show that the IPSO-EKF algorithm can estimate the model parameters and SOC of battery accurately,and correct the state variable initial error.

electrical engineering；lithium battery；state of charge；model parameter；particle swarm optimization algorithm；extended Kalman filter

TM911

A

1000-1093（2014）10-1659-08

10.3969/j.issn.1000-1093.2014.10.021

2014-01-10

军队预先研究项目（40401010101）

项宇（1987—）,男,博士研究生。E-mail：519266224@qq.com；马晓军（1963—）,男,教授,博士生导师。E-mail：maxiaojun_zgy@163.com