模型尺寸对地铁隧道动力响应数值分析的影响

胡显燕， 朱宏平， 王丹生， 宋金强

(1.华中科技大学 土木工程与力学学院，湖北 武汉 430074；2.湖北第二师范学院 建材系，湖北 武汉 430205)

1 研究背景

目前我国北京、上海、广州、武汉等多个大城市已经建成或正在建设地铁项目，城市轨道交通地下结构已经成为基础设施建设的重点，很多研究单位和学者对城市轨道交通地下结构做了大量的试验研究工作。李德武通过模拟列车竖向振动荷载，用有限元法分析列车振动荷载作用下隧道衬砌的响应，并评价其安全性和稳定性[1]。唐益群等人利用室内试验结果确定土体的动弹性模量，采用数值模拟方法计算饱和软粘土地区地铁振动荷载作用下隧道周围土体的变形[2]。Urgar和Kurzweil等通过给定不同列车、轨道、隧道及建筑物类型的修正参数，来预测不同地点由于地铁列车运营引起的环境振动影响。随后出现数值模拟、实验室试验和现场测试相结合的方法，隧道衬砌结构的动力响应及健康诊断已经成为国内外研究的热点问题[3～11]，日本从80年代起，在铁路隧道、水工隧道中引入了健全度概念，对结构的使用寿命进行评估。美国采用结构损伤度的概念对结构损伤进行评估，目前取得了较大的进展。

本文以上海地铁1号线为例，用有限元方法构建三维实体隧道模型，模拟列车通过隧道的动力荷载，对运营期间的隧道结构进行数值分析，可为实际工程的监测分析提供理论依据；并选用不同尺寸的隧道模型进行分析，从中总结模型尺寸对计算结果的影响，以便为实际结构的理论计算选择可靠的计算模型提供参考。

2 理论介绍

2.1 边界条件

列车振动所致结构振动分析一般考虑土层半无限空间，由于土的阻尼衰减，不需要考虑下部基岩的影响。在截断边界上采用如下人工边界条件：模型底部取为竖向固定、水平自由的边界，4个侧面采用自由场边界条件，顶面采用自由边界[12]。

2.2 列车荷载模拟

很多学者对列车荷载的模拟采用简化公式，对于列车在不平顺轨道上行驶的情况，竖向激振荷载可用一个激振力函数来模拟[13]，表达式为

F(t)=p0+p1sin(ω1t)+p2sin(ω2t)+

p3sin(ω3t)

式中，p0为车轮静载，p1，p2，p3分别为按行车平顺性，按作用到线路上的动力附加荷载，以及波形磨耗三种控制条件的振动荷载典型值。

汪杰等通过分析列车振动力变化曲线的频率，得到列车荷载的模拟表达式[14]，该表达式简单，运算速度快，具有较高的可靠性，本文将采用此表达式作为列车荷载：

P(t)=157.36+1.63sin(0.697t+1.183)+2.28sin(1.474t+1.855)+2.83sin(104.722t+3.506)+2.28sin(208.74t+3.735)

(2)

2.3 基本假定

数值模拟时采用下列基本假设：(1)将土层进行加权平均，按均质土层考虑；(2)在动力作用下，土体和隧道不发生脱离和相对滑动；(3)土体和隧道受一致激励；(4)隧道和地层结构采用弹性阶段模拟计算。

3 工程实例

上海地铁盾构隧道埋深在8～15 m，采用通缝拼装形式，管片环由6块管片拼装而成(一块封顶块F、两块邻接块L、两块标准块B和一块拱底块D，圆心角分别对应16°、4×65°和84°，如图1)。上海地铁单圆通缝隧道管片厚度350 mm，管片环外径为6.2 m，管片由C55高强混凝土预制，抗渗等级为1 MPa，管片宽度为1 m。

图1 隧道衬砌结构模型

4 数值模拟

运用ANSYS有限元软件建模分析，衬砌结构用solid65单元模拟，土体用solid45单元模拟。隧道长度取50 m，按1 m划分纵向单元，如图1(b)。隧道中心标高为-15 m，衬砌结构选用C55，土体选择埋深在-14 m左右的粘土层，粘聚力为18 kPa，内摩擦角17°，材料常数取值如表1所示。

表1 材料物理力学参数

数值分析中，隧道结构采用整体建模法，未考虑管片环之间的连接形式，隧道结构刚度取折减系数0.8。为了分析模型尺寸对隧道结构动力响应的影响，采用五种模型尺寸进行分析，见表2。

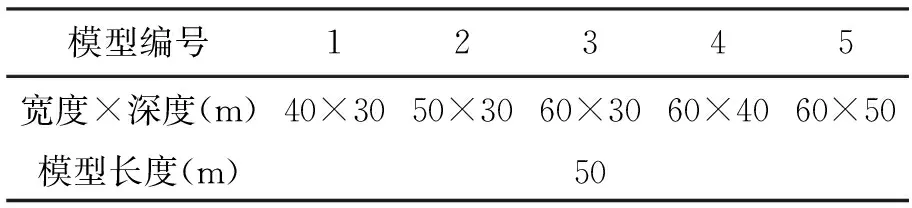
表2 模型尺寸

4.1 列车荷载模拟

列车由拖车和动车组成，拖车自重32 t；动车自重38 t。一列6节编组列车总长为139.48 m。列车定距15.7 m，轴距2.5 m。轨道参数：采用60 kg/m的重轨，轨距为1435 mm。轨枕间距0.595 m。列车最高时速为80 km/h，运营时速一般为60 km/h左右。假设列车从隧道左端行驶至隧道右端，速度υ=60 km/h，长度取50 m，经过隧道需要时间3 s。列车振动荷载模拟如图2。

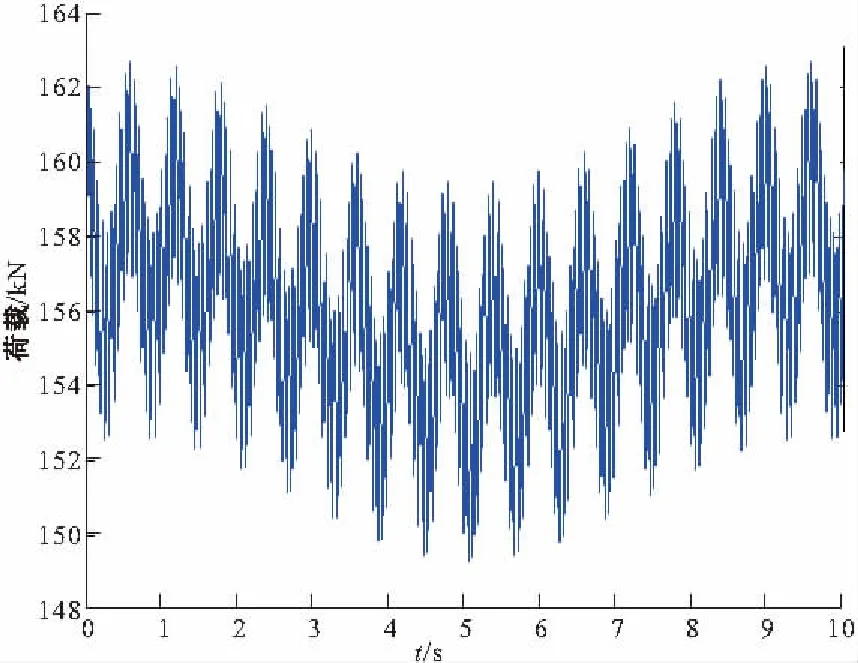
图2 列车荷载模拟

4.2 隧道衬砌结构的加速度响应

在列车荷载的作用下，管片接缝是容易发生损伤的部位，文中选择衬砌结构底部即管片6部分，和衬砌结构顶部即管片1部分(具体参考图1)在环向接缝处的受力变形进行比较，按照列车行进的路线分别研究衬砌结构的起始端，中段，末端的节点响应。主要从x、y，z方向的位移和加速度值随时间的响应，分析列车行进过程中结构的受力情况。首先分析衬砌结构底部，即管片6部分的环向接缝处节点加速度值随时间的响应。

图3～5为不同模型隧道衬砌结构的底部在x方向加速度随时间的响应图谱，其较大值列于表3。

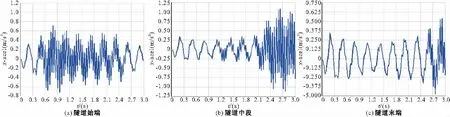
图3 衬砌结构底部 x方向加速度-时间谱(模型3)

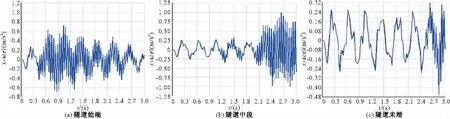
图4 衬砌结构底部 x方向加速度-时间谱(模型4)

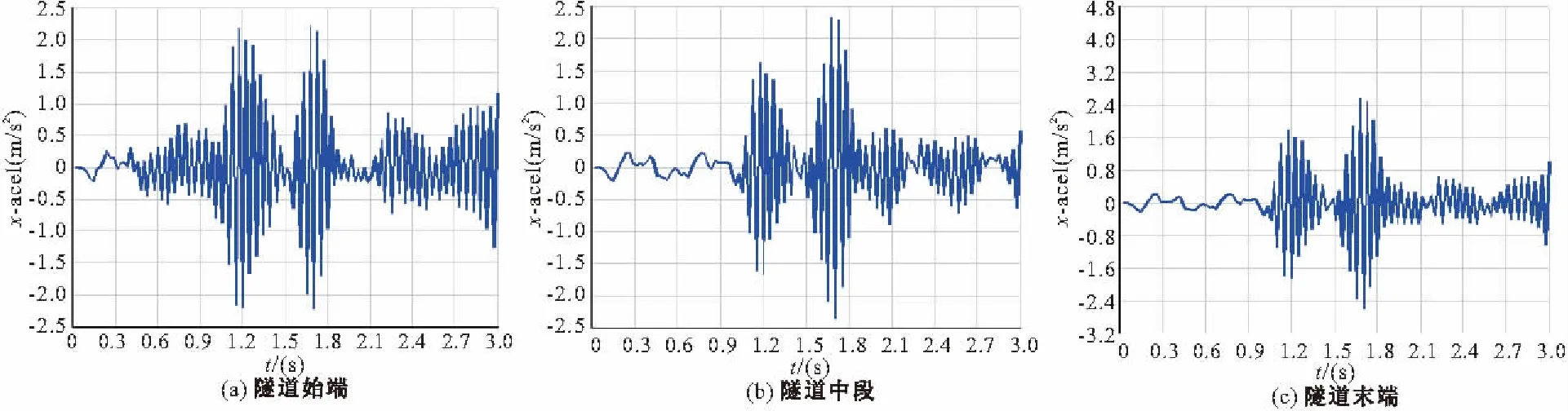
图5 衬砌结构底部 x方向加速度-时间谱(模型5)

模型衬砌结构底部加速度值/(m·s-2)始端中段末端模型30.580.960.54模型40.690.910.75模型52.222.352.58

通过比较发现，模型深度不变，宽度逐渐增加，三个模型的变化规律一致，距离列车越近，加速度响应值的变化越大；起始段的加速度值随着尺寸的增加而有所减小，而列车进入到中段或末端，尺寸的变化影响并不大。如果宽度不变，深度加大时，对于隧道底部(即管片6部分接缝处)，沿x方向的加速度值增大，而模型5的加速度响应明显不同于前面4个模型。

图6显示了衬砌结构底部在y方向的加速度值随时间的响应。模型3的较大加速度值为5.8 m/s2；模型4的较大加速度值为8.4 m/s2；模型5的较大加速度值为10.7 m/s2；从分析结果看到，衬砌结构在列车荷载作用下y方向位移和加速度沿着隧道始端到末端变化量很小，随着深度的加大，衬砌结构底部y方向的加速度响应增大。在三维受力分析中y方向的位移响应和加速度响应均为最大影响因素。

图6 衬砌结构底部 y方向的加速度-时间谱

图7 衬砌结构底部z方向的加速度-时间谱

图7显示了隧道衬砌结构底部和顶部在z方向加速度随时间的响应图谱，从上至下，分别表示隧道始端，隧道中段和隧道末端的加速度图谱。模型5底部z方向的较大加速度值0.08 m/s2；顶部的较大加速度值0.02 m/s2；衬砌结构在z方向的加速度响应值在隧道中段最大，顶部的加速度响应值较小。在三维实体分析中，z方向的位移响应值最小，但在实际结构中不可忽视。

图8显示了衬砌结构顶部在x方向加速度随时间的响应。分析结果显示，在列车荷载作用下，衬砌结构顶部从起始端到末端的加速度值和变化规律都相似。模型2的较大加速度值为0.10 m/s2；模型4的较大加速度值为0.07 m/s2；模型5的较大加速度值为0.89 m/s2；可以看出，模型宽度的影响较小。而模型宽度不变，深度增加时，衬砌结构顶部管片的加速度响应值增大。

图8 衬砌结构顶部 x方向加速度-时间谱

4.3 隧道衬砌结构的位移响应

图9和10显示了衬砌结构环向接缝顶部和底部在x,y,z三个方向上的位移随时间的响应谱。模型4顶部沿x，y，z三方向的较大位移分别为：0.09 mm，79 mm，2.5 mm；模型5底部沿x，y，z三方向的较大位移分别为：1.5 mm，126 mm，3.1 mm；从计算结果可以看出，衬砌结构沿y方向受车辆振动振幅影响最大，沿z方向振幅最小，隧道顶部x方向位移量较小。衬砌结构底部的位移响应较大，而顶部的响应相对较小，但是竖向的响应较大。宽度不变，深度加大，位移响应也会增大。

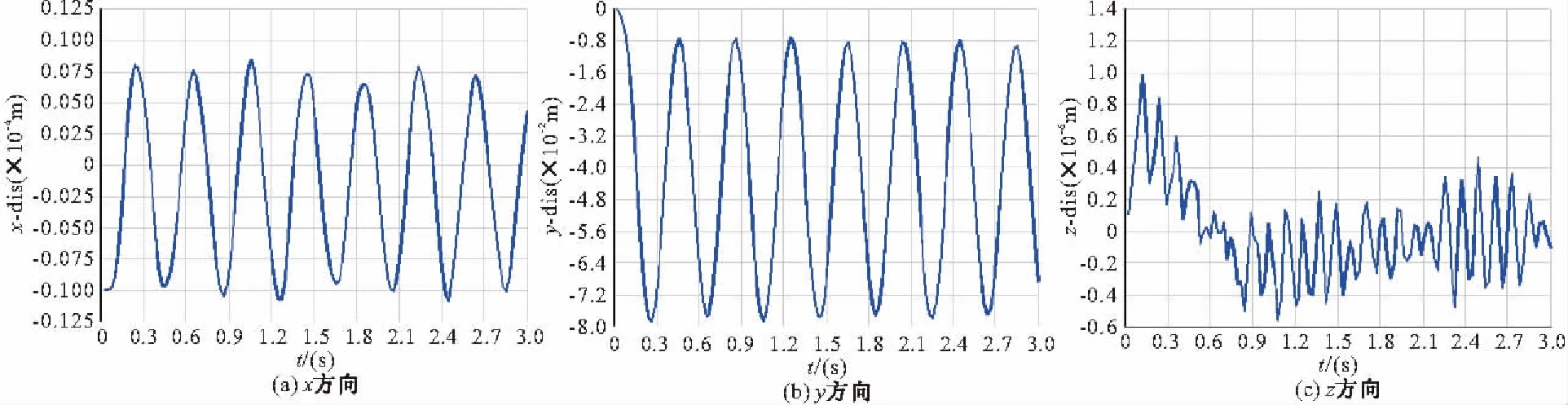
图9 模型4 顶部位移-时间谱

图10 模型5 底部位移-时间谱

4.4 隧道结构变形分析

图11显示了模型5模拟的隧道衬砌结构沿x，y，z方向的变形，单独分析衬砌结构时，x方向位于衬砌结构侧部(即5部分，参考图1)，由于列车荷载有相位的变化，因此衬砌结构并不是两侧对称，而是一侧偏大，一侧偏小；y方向的最大位移值发生在衬砌结构的底部，而顶部的位移最小；z方向的位移很小，沿纵向分布不均匀，和列车荷载时程有关系。表4列出了各模型在x，y，z方向的较大变形值。

图11 模型5变形情况

mm

从表4看出，随着宽度的增大，x，y方向的变形增大，随着深度的增加，变形增大更明显，但超过一定深度，变形量反而减小。5个模型相比较，模型4的变形明显增大。

5 结 论

(1)建立模型时，要考虑到尺寸的变化对衬砌结构的动力响应的影响。理论上，深度增加，位移和加速度响应增大，其中y方向的位移和加速响应都最大，x方向的加速度响应变化较大，位移响应其次；在z方向上也会影响加速度响应值，但是z方向的位移值很小，考虑不多；衬砌结构底部的动力响应较大，顶部的竖向动力响应也较大。

(2)在列车振动荷载作用下，衬砌结构沿y方向的变形量最大，但是x方向和z方向的变形量在实际工程中不可忽视。深度增加，变形量先增大后减小。模型选择时，建议宽度边界取到隧道尺寸的8倍左右，深度边界取到隧道尺寸的6倍左右。通过数值模拟展示衬砌结构在列车荷载作用下的受力变形特征，为实际工程的健康监测与损伤监测提供理论依据。

[1] 李德武.列车振动对隧道衬砌影响的分析[J].兰州铁道学院学报,1997,16(4):24-27.

[2] 唐益群，栾长青，张 曦，等.地铁振动荷载作用下陷隧道土体变形数值模拟[J].地下空间与工程学报, 2008,4(1):105-110.

[3] 王田友.地铁运行所致环境振动与建筑物隔振方法研究[D].上海：同济大学,2007.

[4] Hatzigeorgiou G D, Beskos D E. Soil-structure interaction effects on seismic inelastic analysis of 3-D tunnels[J]. Soil Dynamics and Earthquake Engineering, 2010, 30(9): 851-861.

[5] Hussein M F M, Hunt H E M. A numerical model for calculating vibration due to a harmonic moving load on a floating-slab track with discontinuous slabs in an underground railway tunnel[J]. Journal of Sound and Vibration, 2009, 321(1): 363-374.

[6] Galvin P, Francois S, Schevenels M, et al. A 2.5 D coupled FE-BE model for the prediction of railway induced vibrations[J]. Soil Dynamics and Earthquake Engineering, 2010, 30(12): 1500-1512.

[7] 刘维宁，张昀青.轨道结构在移动荷载作用下的周期解析解[J].工程力学,2004,21(5):100-102.

[8] Jones C J C, Sheng X, Petyt M. Simulations of ground vibration from a moving harmonic load on a railway track[J]. Journal of Sound and Vibration, 2000, 231(3): 739-751.

[9] Shamalta M, Metrikine A V. Analytical study of the dynamic response of an embedded railway track to a moving load[J]. Archive of Applied Mechanics, 2003, 73(1-2): 131-146.

[10] Ding D, Gupta S, Liu W, et al. Prediction of vibrations induced by trains on line 8 of Beijing metro[J]. Journal of Zhejiang University SCIENCE A, 2010, 11(4): 280-293.

[11] 刘卫丰.地铁列车运行引起的隧道及自由场动力响应数值预测模型研究[D].北京：北京交通大学,2009.

[12] 王国波.软土地铁车站结构三维地震响应计算理论与方法的研究[D].上海:同济大学,2007.

[13] 莫海虹，邓飞皇，王家辉.营运期地铁盾构隧道动力响应分析[J].岩石力学与工程学报,2006,25(s2):3507-3512.

[14] 汪 杰，宋瑞刚，袁天成，等.地铁列车荷载的仿真模拟[J].上海工程技术大学学报,2011, 25(3):213-216.