水平管内汽液两相流流型及换热特性数值模拟

李书磊，蔡伟华，李凤臣

水平管内汽液两相流流型及换热特性数值模拟

李书磊，蔡伟华，李凤臣

（哈尔滨工业大学能源科学与工程学院，150001哈尔滨）

为研究水平管内相变汽液两相流动流型变化，使用VOF模型和RSM湍流模型对其进行了数值模拟，分析了水平管内对流换热、压降及流型的变化.模拟结果表明：VOF模型和RSM湍流模型可用于模拟两相流流型中的泡状流、分层流、波状流、弹状流以及环状流；模拟结果与Mandhane流型图基本吻合；对流换热系数及压降与已有关联式吻合较好.

汽液两相流；流型；VOF；雷诺应力模型

气液两相流动是指在同一流动体系中，同时存在气液两相共同流动的流动现象.它是最为常见的多相流动现象之一.流型是指流体介质在共同流动时相的分布状况，它直接关系到流体的压降损失机理以及传质传热特性.气液两相流根据物质组分的不同，可分为单组分气液两相流，如水蒸气-水两相流（又称汽液两相流）和双组分气液两相流，如空气-水两相流等［1］，根据流动环境的不同，可分为管内两相流和管外两相流.目前，管内气液两相流的研究主要采用实验和数值模拟，而对有相变过程的管内汽液两相流则主要偏重于实验研究.王维城等［2］、陈剑波等［3］、邢玉雷等［4］、Cavallini等［5］和Yan等［6］分别对管内沸腾和蒸汽凝结换热进行了实验研究，结果表明：换热系数与流动状态密切相关，不同流态的换热机理不同.Yang等［7］、Wu等［8］分别采用VOF模型及Realize k-ε湍流模型和欧拉两流体对水平蛇形管内的沸腾汽液两相流进行了数值模拟研究.结果表明：流道内温度分布取决于相分布，高温总是出现在蒸汽区；同时重力及弯曲处离心力对管内流型的分布影响较大，从而影响了温度场的分布，与实验吻合较好.韩晓霞等［9］、陈高飞等［10］、Park等［11］和王树立等［12］分别对水平管内沸腾换热和气液两相螺旋流的压降规律进行了实验研究.结果表明：流型是影响摩擦压降规律的主要因素，同时两相摩擦压降随质量流量、质量含气率的增大而增大；Yang［7］、Wu［8］等的数值模拟研究则表明：气液分界面、流量及重力是影响压降分布的主要因素.在对水平管内流型研究方面，吴业正［13］等提出了用温度波动规律判别水平管内蒸发时流型的新方法.de Sampaio［14］等对水平管内分层气液两相流进行了数值模拟研究.结果表明k-ω模型可以用来模拟分层气液两相流.Tsuji［15］、IssaI［16］等分别采用朗格朗日方法和欧拉法两流体模型对水平管内的段塞气液两相流的形成和发展进行了数值模拟研究.结果表明：段塞流是在分层流的基础上液体向上波动形成的.De Schepper［17］等采用VOF模型及标准k-ε湍流模型对水平换热管中烃的蒸发裂化过程进行了数值模拟，得到了分层流和环状流.张金红［18］和宫莎莎［19］等则分别对水平管内气液两相流流型进行了实验和数值模拟研究，结果表明：水平管内流型与Mandhane流型图吻合较好.但是到目前为止，数值模拟对水平管内汽液两相流压降、换热和流型同时进行研究的报道相对较少，尚未建立起较为完善的带换热过程的水平管内汽液两相流流型及流动与换热特性的数值模拟方法.

本文基于Fluent软件提出了一种可以广泛应用于不同干度、不同流量、不同流型的带相变过程的水平管内汽液两相流流型及流动与换热特性的数值模拟研究方法，模拟了水平管内水-水蒸气冷凝两相流动，分析了其流型和流动与换热特性，并通过模拟结果与已有关联式和流型图的对比验证了其准确性.

1 水平管内典型流型

近年来，有学者提出了从多相流中流动介质的连续性出发进行流型的划分，即将介质的形态分为连续的、间歇的和弥散的.水平管内的气液两相流流型划分方法如图1所示，流型示意图如图2［20-21］.

图1 按介质的连续性进行划分的水平管内气液两相流流型［20］

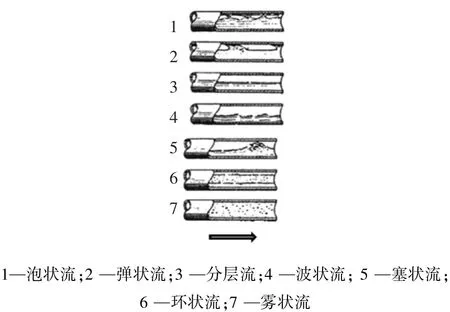
图2 水平管中的气液两相流的不同流型［21］

1）泡状流.水平管内的泡状流由于重力影响，小气泡大部分位于管上部.

2）塞状流.当气流量增加时，小气泡合并成气塞，形成柱塞状流动结构，柱塞状倾向于沿管子上部流动.

3）分层流.当气液两相流量均很小时，会发生分层流动，气相在上，液相在下，气液分界面平滑，两相分开流动.

4）波状流.当气相流量较大时，气液两相分界面上会出现波动，形成波状流动结构.

5）弹状流.当液流量增大时，气液两相流的流动结构可以从波状流转变为弹状流，此时气液界面由于剧烈波动而在某些部位直接和管子上部接触，将位于管子上部的气相分隔为气弹形成弹状流动.

6）环状流.在水平流动时，气液两相流的环状结构出现于气相流量较高的工况，管壁上有液膜，管子中心部分为带液的气核，但由于水平流动时重力的影响作用，下部管壁的液膜要比上部管壁厚.

7）雾状流.在环状流的基础上，当气流速度继续增大时，液膜将被气流吹干，液相以液滴的形式被气流夹带往前流动.

流型图是用于流型识别及流型转换判断的重要手段之一.Mandhane提出了水平管流型图［22-23］，如图3所示.图中vl和vg分别表示液体折算速度和气体折算速度.

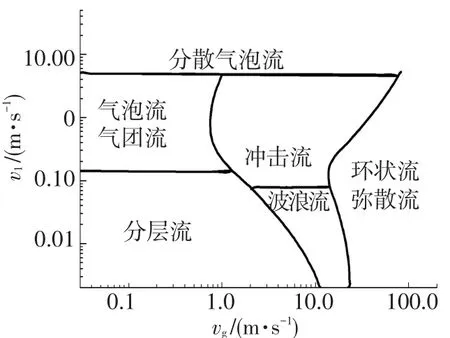
图3 Mandhane提出的水平管流型图

2 计算模型与数值模拟方法

2.1计算模型

本文主要研究水平圆管内水和水蒸气冷凝两相流.选取内径为12 mm，长为4 m的水平直圆管进行数值模拟.

2.2控制方程

连续性方程：

两相流模型选用VOF模型，其控制方程为容积比率方程：

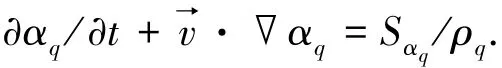
式中Sαq为质量源项，由用户自定义函数UDF给出.

容积比率方程不是为主相求解的，主相容积比率的计算基于如下的约束：

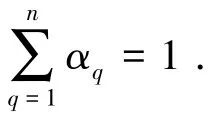
动量方程：

式中F➝为体积力.

能量方程：

式中：keff为有效热传导系数，Sh为能量源项，通过用户自定义函数UDF给出.

湍流模型采用雷诺应力（RSM）湍流模型，其控制方程为

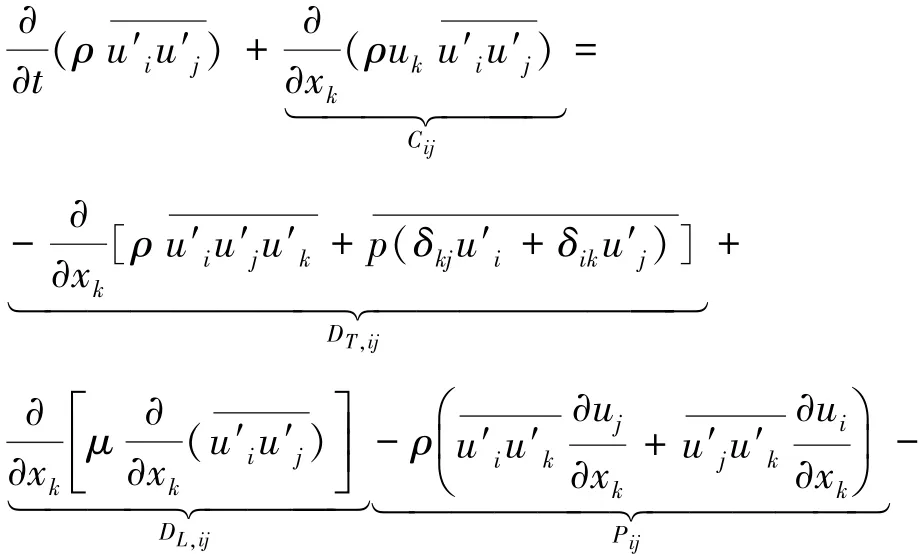
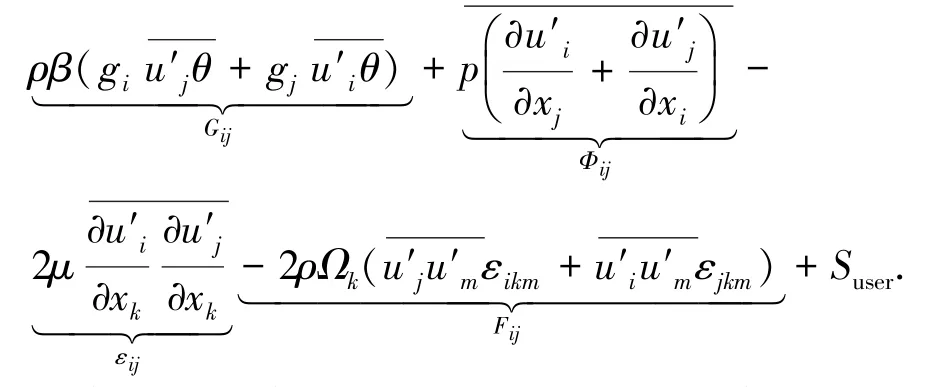
式中：Cij为湍流动能对流项，DT，ij为湍流动能梯度扩散项，DL，ij为湍流动能分子扩散项，Pij为湍流动能应力生成项，Gij为湍流动能浮力生成项，Φij为湍流动能压力应变项，εij为湍流动能耗散项，Fij为湍流动能旋转生成项，Suser为湍流动能用户自定义项.

2.3数值求解

采用结构化网格对计算区域进行划分，同时在边壁处进行加密.启动能量方程，两相流计算选用VOF模型，湍流模型选取RSM湍流模型进行计算，采用标准壁面函数处理近壁区域流动.入口采用质量流量入口边界条件，出口采用自由出流.压力参考点设置在入口处.壁面采用定热流无滑移壁面边界条件.

数值离散格式及计算方法简述如下：压力采用PRESTO！格式；动量方程、雷诺应力方程、能量方程均采用二阶迎风格式，容积比方程采用Geo⁃Reconstruct格式；采用PISO算法对代数方程进行离散求解.根据数值模拟工况，由Refprop软件获取物性参数.

3 网格无关性验证

首先进行网格无关性验证.分别选取20万、25万、40万和50万总网格数来数值计算同一流动工况，水和水蒸气管内流动，进口压力和温度为5 MPa和537.09 K，进口质量流率为60 kg／（m2·s），干度为0.4.网格尺寸及模拟结果如表1所示.

从表1可知：沿线拉伸尺寸相同时，面网格尺寸对模拟结果影响较大；面网格尺寸相同时，沿线拉伸尺寸对模拟结果影响不大；模拟值与关联式的结果比较可知，当面网格尺寸为1 mm时，二者吻合更好，故选用网格系统1和2均可；由于一般情况下网格要求沿线拉伸尺寸与面网格尺寸之比应＜5∶1，所以最终选用网格系统1进行数值模拟.

表1 网格无关性验证试验表

4 对流换热与压降结果分析

将所有模拟工况在Mandhane流型图标出，如图4所示.图中m表质量流率.

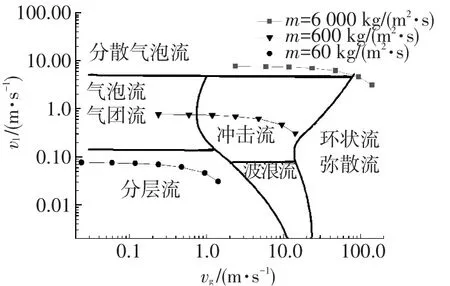
图4 模拟工况点在Mandhane流型图中的分布

将摩擦压降梯度模拟结果与杜克勒1法压降关联式［24-25］及Baker环状流压降关联式进行对比分析；换热系数模拟结果与Collier［26］，Akers［27］和Boyko⁃Kruzhilin［28］所提出的对流换热关联式进行对比分析.下面将给出压降和换热关联式及其使用条件.

杜克勒1法压降关联式［24-25］如下：

该压降关联式是基于均相流假设得到的.式中：ρ、v和μ分别表示密度、速度和黏度，R e为雷诺数，d为管径，x为干度，下标l、g和m分别代表液相、气相和混合相.

Baker环状流压降关联式如下：

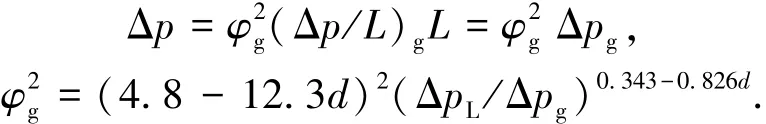
该关联式仅适用于环状流.

Akers对流换热关联式［26］如下：

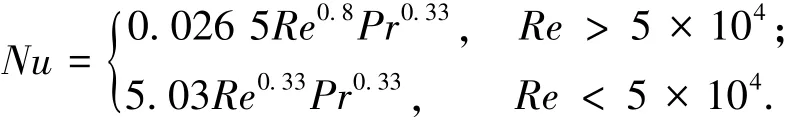
该对流换热关联式的系数根据对丙烷和R12在15.8 mm水平管内冷凝的实验测量确定.丙烷的测量数据如下：质量流量：1.62～175.00 kg／（m2·s），压力为2.24～4.21 MPa.

Collier对流换热关联式［27］如下：

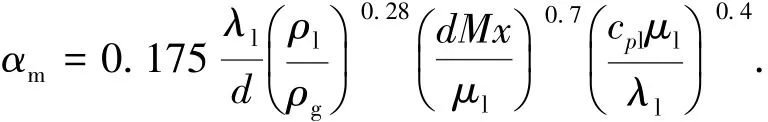
该对流换热关联式的系数是通过蒸汽在垂直管向上流动的实验中得到的，实验测量数据如下：直径为9.52-15.88 mm，最高压力为550 kPa，含气率为0～0.659 kg／kg，质量流率为134～1 077 kg／（m2·s）.

式中：λ、cp和α分别表示导热系数、比热容和对流换热系数，M表示质量流率.

Boyko⁃Kruzhilin对流换热关联式［28］如下：

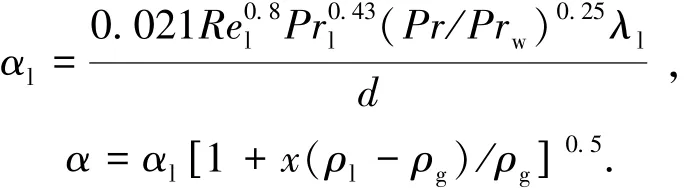
该对流换热关联式是基于环状流推导得到的，与蒸汽-水部分冷凝实验的测量结果进行比对，实验管材为钢管和铜管，管径为8.0 mm，压力为0.7～22.0 MPa.式中下标w代表壁面.

4.1模拟摩擦压降梯度与关联式的比较

图5给出了不同质量流量不同干度下摩擦压降梯度与杜克勒1法及Baker环状流压降关联式的对比结果.

图5 不同流量、干度下模拟与杜克勒1法及Baker环状流摩擦压降梯度的比较

从图5可知，模拟得到的摩擦压降梯度随着干度的增大而增大，且随着流量的增大而增大，这与杜克勒1法的趋势一致，误差在20%以内；但随着干度和流量的增大，流型呈环状流状态，模拟得到的摩擦压降值与杜克勒1法偏离逐渐增大，但此时模拟结果与Baker环状流压降关联式吻合较好.

4.2模拟对流换热系数与关联式的比较

图6给出了不同质量流量不同干度下对流换热系数与不同关联式的对比结果.

从图6可知，模拟得到的对流换热系数随着干度的增大而增大，且随着流量的增大而增大，这与关联式趋势一致；在小流量下（m＝60 kg／（m2·s）），对流换热系数与Akers关联式的结果吻合较好；在中等流量下（m＝600 kg／（m2·s）），对流换热系数与Collier关联式的结果吻合较好；在大流量下（m＝6 000 kg／（m2·s）），对流换热系数与Boyko⁃Kruzhilin关联式吻合较好.

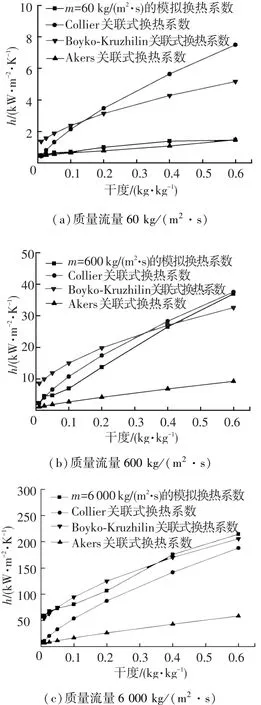
图6 不同流量、干度下模拟与Akers等关联式换热系数的比较

除个别工况外，对流换热系数模拟结果与关联式结果的偏差均在±30%以内.

综上可知：在不同干度，不同流量下模拟得到的压降梯度和对流换热系数基本上与已有关联式吻合较好，说明该数值方法具有较好的可行性.

5 水平管内汽液两相流流型模拟结果

5.1小流量（m＝60 kg／（m2·s））下的模拟结果

图7给出了质量流率m＝60 kg／（m2·s）时不同干度下y＝0截面整体及出口端局部放大的气体体积分数分布.

从图7可知，由于总质量流率较小，汽液流速一直都很小，受重力作用，汽液两相分离.从整体上看，除入口端很短一段不稳定流型区外，均呈分层流状态.从出口端局部放大图上看，该流量下形成的分层流分界面平整，且随着干度的增大，水平管底部液体厚度逐渐变薄；当干度达到0.6时，由于此时水量非常少，水在下管壁上出现不连续现象，从而形成了分散分层流.上述流型模拟结果与Mandhane流型图完全吻合.

5.2中等流量（m＝600 kg／（m2·s））下的模拟结果

图8给出了质量流率m＝600 kg／（m2·s）时不同干度下y＝0截面整体及出口端局部放大的气体体积分数分布.

从图8可知，由于总质量流率增大，汽液流速均比m＝600 kg／（m2·s）工况下的要大，同样受重力作用，汽液两相分离.从整体上看，入口端气液互相掺杂严重，沿流动方向流型逐渐趋于稳定，在出口段形成较稳定的流型；同时随干度的增大，入口流型不稳定区先增大后减小；从出口端局部放大图上看，当干度很小时，水量较大，导致部分水面波动到上管壁，引起气体被分割，从而形成弹状流；随着干度的增大，水量减小，液面下降，但由于此时气体流速较大，气液分界面不平整，从而形成波状流；随着干度继续增大，水蒸气流速继续增大，液体被吹到上管壁，从而形成环状流；当干度达到0.6时，水量已经非常小了，壁面上只有局部地方出现液滴，液体在管壁分布不再连续，形成了局部环状流.上述中等流量下的流型模拟结果与Mandhane流型图存在一定的偏差，这可能是由于采用VOF模型模拟两相流流型时没有完全考虑相间作用的缘故.

5.3大流量（m＝6 000 kg／（m2·s））下的模拟结果

图9给出了质量流率m＝6 000 kg／（m2·s）时不同干度下y＝0截面整体及出口端局部放大的气体体积分数分布.

图7 m＝60 kg／（m2·s）时不同干度下y＝0截面水蒸气体积分数分布

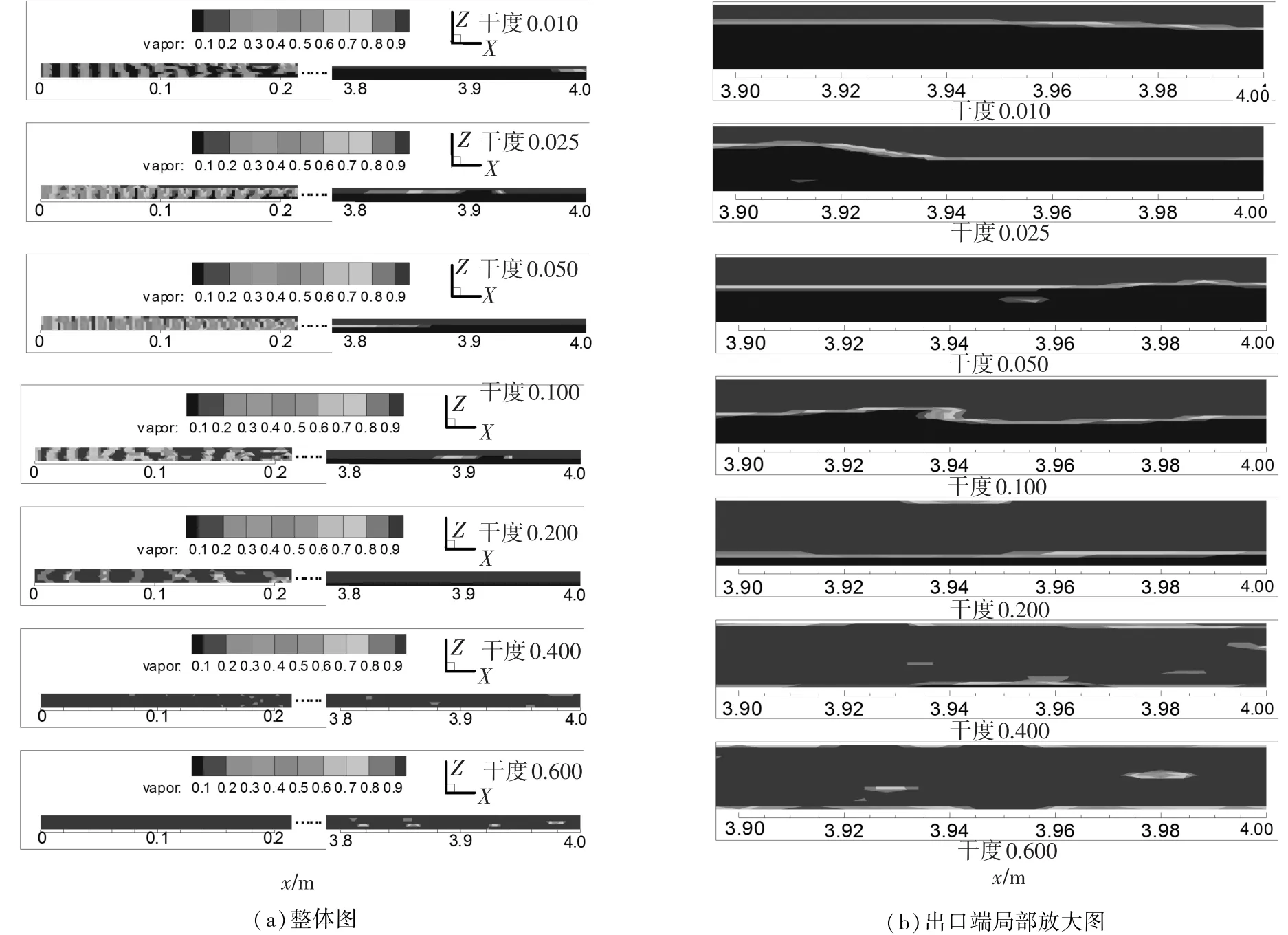
图8 质量流量为600 kg／（m2·s）时不同干度下y＝0截面水蒸气体积分数分布

图9 质量流量为6 000 kg／（m2·s）时不同干度下y＝0截面上气体体积分数分布图

从图9可知，由于总质量流率非常大，汽液流速也非常大，此时流动受重力作用影响较小.从整体上看，入口端气液互相掺杂严重，沿流动方向流型逐渐趋于稳定，在出口段形成较稳定的流型；同时随干度的增大，入口流型不稳定区逐渐减小.从出口端局部放大图上看，当干度很小时，水量较大，水蒸气分散在水中，形成了分散气泡流；随着干度增大，气泡聚合到一起，形成了环状流，且壁面液膜厚度随干度增大而减小；当干度达到0.6时，由于此时液体量很小，壁面上只有局部地方出现液滴，液体在管壁分布不再连续，形成了局部环状流.上述流型模拟结果与Mandhane流型图基本吻合.

6 结 论

1）模拟得到的摩擦压降梯度在小流量小干度，即流态呈现为非环状流时，与杜克勒1法吻合较好；在大流量大干度，即流态呈现为环状流时，与Baker环状流压降关联式吻合较好.

2）在流量较小时，模拟得到的对流换热系数与Akers关联式吻合较好；在中等流量下，对流换热系数与Collier关联式吻合较好；而在大流量下，对流换热系数与Boyko⁃Kruzhilin关联式吻合较好.

3）数值模拟了水平管内多种不同流型：如连续流（分层流，波状流，环状流）、间歇流（弹状流）和弥散流（泡状流）.除间歇流（冲击流）外，其他流型模拟结果均与Mandhane流型图中给出的流型分布吻合较好.

［1］林宗虎.管路内气液两相流特性及其工程应用［M］.西安：西安交通大学出版社，1992.

［2］王维城，刘志坚，王补宣，等.强化水平管内沸腾换热的实验研究［J］.工程热物理学报，1991，12（1）：54-58.

［3］陈剑波，蔡祖恢，丁一鸣，等.R12在水平管内流动沸腾换热实验研究［J］.上海机械学院学报，1992，14（3）：1-10.

［4］邢玉雷.真空水平管内蒸汽凝结换热实验研究［D］.大连：大连理工大学，2008.

［5］CAVALLINI A，DEL COL D，DORETTI L，et al.Heat transfer and pressure drop during condensation of refrigerants inside horizontal enhanced tubes［J］.International Journal of Refrigeration，2000，23（1）：4-25.

［6］YAN Y Y，LIN T F.Evaporation heat transfer and pressure drop of refrigerant R-134a in a small pipe［J］.International Journal of Heat and Mass Transfer，1998，41（24）：4183-4194.

［7］YANG Z，PENG X F，YE P.Numerical and experimental investigation of two phase flow during boiling in a coiled tube［J］.International Journal of Heat and Mass Transfer，2008，51（5）：1003-1016.

［8］WU H L，PENG X F，YE P，et al.Simulation of refrigerant flow boiling in serpentine tubes［J］.International Journal of Heat and Mass Transfer，2007，50（5）：1186-1195.

［9］韩晓霞，南晓红，刘咸定，等.R290与R404A在水平管内沸腾换热的压降研究［J］.制冷学报，2006，27（2）：17-20.

［10］陈高飞，公茂琼，沈俊，等.水平管内二氟乙烷两相流动摩擦压降实验研究［J］.物理学报，2010，59（12）：8669-8675.

［11］PARK C Y，HRNJAK P S.CO2and R410A flow boiling heat transfer，pressure drop，and flow pattern at low temperatures in a horizontal smooth tube［J］.International Journal of Refrigeration，2007，30（1）：166-178.

［12］王树立，饶永超，魏鸣姣，等.水平管内气液两相螺旋流压降规律实验研究［J］.科学技术与工程，2013，13（3）：559-663.

［13］吴业正，李俊明，李新中，等.用温度波动规律判别水平管内蒸发时流型的实验研究［J］.西安交通大学学报，1995，29（11）：57-63.

［14］de SAMPAIO P A B，FACCINIJ L H，SU J.Modelling of stratified gas⁃liquid two⁃phase flow in horizontal circular pipes［J］.International Journal of Heat and Mass Transfer，2008，51（11）：2752-2761.

［15］TSUJI Y，TANAKA T，ISHIDA T.Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe［J］.Powder Technology，1992，71（3）：239-250.

［16］ISSA R I，KEMPF M H W.Simulation of slug flow in horizontal and nearly horizontal pipes with the two⁃fluid model［J］.International Journal of Multiphase Flow，2003，29（1）：69-95.

［17］de SCHEPPER S C K，HEYNDERICKX G J，MARIN G B.Modeling the evaporation of a hydrocarbon feedstock in the convection section of a steam cracker［J］.Computers＆Chemical Engineering，2009，33（1）：122-132.

［18］张金红.气液两相流流型实验研究［D］.哈尔滨：哈尔滨工程大学，2005.

［19］宫莎莎.水平混输管路流型研究［D］.东营：中国石油大学，2009.

［20］劳力云.气液两相管流流态判别方法的研究［D］.北京：中国科学院力学研究，2001.

［21］陈学俊，陈立勋，周芳德.气液两相流与传热基础［M］.北京：科学出版社，1995.

［22］郭烈锦.两相与多相流动力学［M］.西安：西安交通大学出版社，2002.

［23］林宗虎.变幻流动的科学——多相流体力学［M］.北京：清华大学出版社，2000：69-71.

［24］CICCHITTI A，LOMBARDI C，SILVESTRI M，et al.Two⁃phase cooling experiments：pressure drop，heat transfer and burnout measurements［R］.Milan：Centro Informazioni Studi Esperienze，1959.

［25］DUKLER A E，WICKS M，CLEVELAND R G.Frictional pressure drop in two⁃phase flow：A comparison of existing correlations for pressure loss and holdup［J］.AIChE Journal，1964，10（1）：38-43.

［26］AKERS W W，DEANS H A，CROSSER O K.Condensing heat transfer within horizontal tubes［J］.Chem Eng Prog Symp Ser，1959（29）：171-176.

［27］KLIMENKO V V.A generalized correlation for two⁃phase forced flow heat transfer［J］.International Journal of Heat and Mass Transfer，1988，31（3）：541-552.

［28］NEERAAS B O.Condensation of hydrocarbon mixtures in coil⁃wound LNG heat exchangers，tube⁃side heat transfer and pressure drop［R］.Trondheim，Norway：Norwegian Institute of Technology，1993：172-179.

（编辑杨 波）

Numerical simulation on flow pattern and heat transfer of vapor⁃liquid two⁃phase flow in horizontal pipe

LI Shulei，CAI Weihua，LI Fengchen
（School of Energy Science and Engineering，Harbin Institute of Technology，150001 Harbin，China）

In order to study the evolution of the flow pattern in a phase⁃transition vapor⁃liquid two⁃phase flow in a horizontal pipe，numerical simulation based on volume⁃of⁃fluid（VOF）model and the Reynolds stress turbulence model（RSM）was performed.The characteristics of convective heat transfer，pressure drop and evolution of flow patterns in the simulated horizontally pipe⁃flow were analyzed.It was obtained that the VOF model and RSM model can be used to simulate bubble flow，stratified flow，wavy flow，slug flow and annular flow.The simulated two⁃phase flow patterns are in agreement with the Mandhane flow pattern map.Furthermore，the simulated heat transfer coefficient and pressure drop are also in good agreements with the existing correlations.

vapor⁃liquid two⁃phase flow；flow pattern；VOF；reynolds stress turbulence model

O359

A

0367-6234（2014）08-0057-08

2013-08-13.

国家自然科学基金资助项目（51206033；51276046）；哈尔滨工业大学科研创新基金资助项目（HIT.NSRIF.2011070）.

李书磊（1989—），男，硕士研究生；

李凤臣（1971—），男，教授，博士生导师.

蔡伟华，caiwh＠hit.edu.cn.