一种用于高光谱图像特征提取的子空间核方法

刘振林，谷延锋，张 晔

（哈尔滨工业大学电子与信息工程学院，黑龙江哈尔滨150001）

一种用于高光谱图像特征提取的子空间核方法

刘振林，谷延锋，张 晔

（哈尔滨工业大学电子与信息工程学院，黑龙江哈尔滨150001）

特征提取对于实现高光谱遥感图像的有效信息挖掘和利用以及提高后续分类应用有着重要价值。为了改进降维效果，提出一种子空间调制的核主成分分析方法，将高光谱数据分组特性整合到一个统一的核方法框架中，并构造子空间调制核。子空间调制核依靠特征分组实现了在光谱波段上的稀疏调制，它也是一个数据自适应的核，用于度量高光谱数据样本间的非线性相似性。该方法利用AVIRIS真实高光谱图像进行评估，并且与传统的核方法、光谱加权核方法进行了比较。实验结果表明，基于子空间调制的核方法更充分地利用了波段间复杂相关的物理特性，进而在高光谱图像分类方面的结果好于传统的核方法与光谱加权核方法。

高光谱图像；核方法；数据降维；图像分类；特征提取

近年来高光谱成像技术广泛应用于民用和军用领域。高光谱图像的光谱分辨率一般达到10 nm。这样高的光谱分辨率使得高光谱图像适合于辨别光谱相似的地表覆盖类别。同时，较高的光谱分辨率意味着高光谱数据立方体拥有着巨大的数据量，所以在处理高光谱图像时考虑计算时间和存储资源是很有必要的。在这种情况下，特征提取或降维成为了后续应用过程中的必要手段［1-4］。

考虑到波段间复杂的相关性，Jia等［5］提出了分段主成分变换（segmented principal component transform，SPCT）来提高传统主成分分析（principal com-ponent analysis，PCA）的性能。在SPCT中，首次提出了基于光谱波段间相关性的特征分组，研究表明SPCT在高光谱图像降维方面优于传统PCA方法。SPCT的成功应用表明特征分组能够对不同子空间数据或子数据重要性进行清晰的解释和估计，这样在高光谱图像分析方面更有利用价值。在过去十年中，一些研究发现了核方法在遥感图像处理中的巨大潜力，特别是在高光谱图像分析中。为了更好地挖掘核方法在度量非线性相似性方面的潜力，学者们相继提出了一些改进的核。其中，重要进展包括2个方面［6-12］，如混合核和半监督核。Guo等提出了一个光谱加权核方法，即通过优化泛化误差或者通过评估每个波段的贡献大小来选择一系列特殊的权值，旨在更好地利用SVM技术进行高光谱图像分类［13］。但现有光谱加权核方法未能有效利用高光谱图像特征分组的可分特性。到目前为止，特征分组作为高光谱图像可分特性还没有在核设计中得到充分重视。

本文通过将特征分组整合到核函数设计中，得到一个新的核函数来解决高光谱图像中的降维问题。实质上，高光谱数据可以被近似的视为不同传感器在同一时刻采集到的异构信息，这是因为数据覆盖了不同电磁波波长范围，从可见光到近红外甚至到热红外。考虑到高光谱数据异构特性，提出一个子空间核方法，即子空间调制核主成分分析（简记为SM-KPCA）。在提出的方法中，高光谱数据特征分组用于决定基核的数目。然后，调制因子，例如不同子空间的核的权值，通过不同子空间的波段图像和地物真实图的互信息来决定。此外，比较分析了在降维和分类应用中3种特征分组方法的效果。为了证明提出的SM-KPCA算法的有效性，利用真实AVIRIS高光谱图像进行验证实验。分类精度作为一个主要指标来客观评价该算法的有效性。

1 核方法

给定原始数据空间RL，输入数据X＝{x1，x2，…，xN}。对于高光谱图像x2∈RL，k＝1，2，…，N，可以视为第k个波段图像的向量化。通常，输入空间中的数据并不是线性可分的。核方法将输入数据映射到高维特征空间中，以便使数据在新的空间中线性可分。特征空间表示为F，相应的映射为Ф。非线性映射如下：

通常在特征空间需要做的是计算映射样本的内积。核方法的主要思想是利用一个在输入空间定义的核函数代替特征空间中的内积。核函数定义为

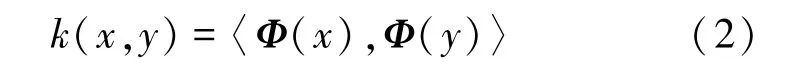
这样，可以通过输入空间的核函数来代替内积的计算，所以映射Ф的形式并不需要明确的给出。方程（2）只是核的一般形式，它可以视为2个样本间的相似性度量。在本文研究中主要采用高斯核。

高斯径向基函数（RBF）：

2 本文算法

2.1 特征加权核

对于遥感中高光谱图像的高维数据，数据的信息来自从可见光到红外的很宽波长范围。所以，在设计核结构时，值得区分不同源的特征。把核叫做特征加权核，它的一般描述如下：

Kw( xi，xj)＝K( X Di，X Dj)＝K( dixi，djxj)（4）式中：X＝[x1x2…xN]，D是数据矩阵X的对角权值矩阵，diag D＝(d1，d2，…，dN)，X Di是XD的第i列。

考虑方程（4）高斯核，方程（3）可重新表示如下：

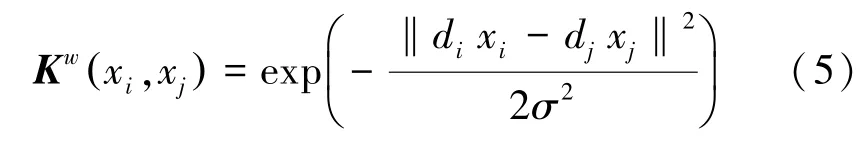
式中：Kw·，·()表示加权高斯核。将带宽参数σ引入到对角矩阵D中，用矩阵Dm代替D。有

根据方程（6）和（7），可以发现新增的对角矩阵D起到调制样本带宽参数σ的作用，带宽参数σ在特征加权核中不再是一个常数。换句话说，在将权值矩阵D或Dm引入到新的核函数之后，特征加权核的带宽参数σ是随着不同光谱特征或光谱波段自适应变化的。在高光谱图像应用中，方程（7）中的核是适应于光谱波段的核。所以分别称Dm和ΔW为调制矩阵和各自全空间的调制向量。

2.2 子空间调制的核PCA

根据方程（7），可以注意到选择好调制向量ΔW就表明特征加权核可以提供较好的样本相似性的非线性度量。本文提出的SM-KPCA包括3个主要部分，即基于光谱波段复杂相关性的特征分组，优化调制向量的确定和子空间调制核的特征值分解。

首先，对原始高光谱数据进行特征分组，即根据相关性或信息度量将原始高光谱数据分割成一些子空间。一般来说，在同一子空间中不同波段的高光谱图像子集有很强的相关性，这表明这些波段图像应该有相同的调制因子。在分完M个子空间后，原始高光谱数据空间S可以写为

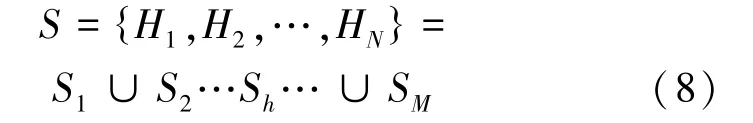
式中：Sh( h＝1，2，…，M，M＜＜N)是S的数据子空间，Hi( i＝1，2，…，N)是第i个波段图像，N是高光谱图像的波段数，并且Si∩Sj＝Ø（Ø是空集）。

用子空间调制向量ΔS代替全空间调制向量ΔW，有

式中：σsh( h＝1，2，…，M)是对应第h个数据子空间Sh的调制向量。即同一子空间Sh的每一波段图像共享σsh。

其次，在本章的后2部分给出了确定子空间调制向量ΔS的方法。

在确定了稀疏子空间调制向量ΔS后，可以获得子空间调制核，并用子空间调制核代替传统的KPCA核矩阵K得到子空间调制KPCA。本章的最后给出传统KPCA简单的介绍。

在特征空间F中，协方差矩阵计算如下：

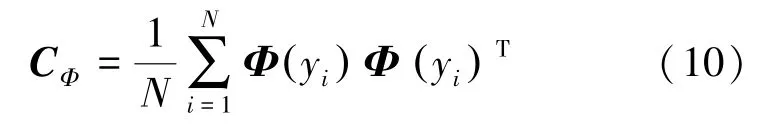
CΦ的特征值分解如下：

式中：V可以由Φyi(){}生成的特征空间F表示：

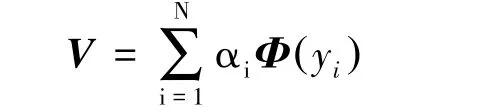
与方程（4）等效的方程可以写为

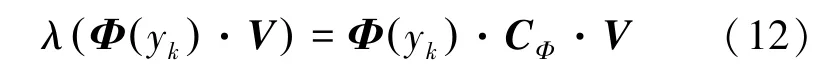
利用核函数代替F中的内积。根据方程（2），一个N×N的核矩阵K计算如下：

得到的结果(λk，αk)需要通过λk(αk·αk)＝1规范化，K需要用中心核矩阵Kc代替。表示如下：

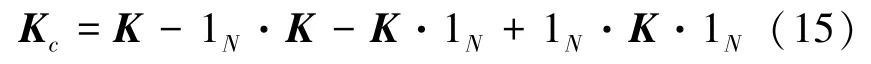
式中：1N是一个N×N矩阵，其元素为1／N。

为了提取核主成分，映射样本Φ(x)可以投影到特征空间中的特征向量Vk上，其可以如下描述：

上面简单介绍了KPCA的基本概念，在子空间调制KPCA中，核由下式给出：

2.3 高光谱图像特征分组

特征分组是在特定的规则下将原始数据的所有光谱波段划分成若干组。一般来说，具有很高相关性的一系列光谱波段会被分到相同的组中，组成子空间数据。本文分析了3种特征分组方法，并用于确定子空间调制核的数目。接下来对这些分组方法进行详细描述。

2.3.1 基于相关性的子空间

光谱波段yi和yj的相关系数由下式计算：

在计算完2个波段光谱相关系数后，高光谱数据的所有N个波段的相关系数矩阵表示为

给定一个光谱波段相关性的可视化度量方法，Indian Pine数据（200个波段）的相关系数矩阵如图1所示。这种基于相关性的波段分组方法是沿着波段逐步进行的。2个连续子空间的边界通过相关系数的预设阈值自动度量。分块过程从第1个波段开始，第1个波段被固定作为第1个子空间的初始波段。然后计算下一个波段与初始波段的相关系数，并与预设阈值比较。如果相关系数高于阈值，那么该波段被认为是当前子空间的元素。相反，则结束当前子空间的扩展，该波段作为下一个子空间的初始波段。同样的操作一直持续到最后一个波段，这样就可以完成对所有波段的特征分组。

2.3.2 基于局部相关的子空间

在文献［14］中，讨论了局部相关系数的概念，它揭示出显著的相关性只存在于相邻的波段之间。借助于光谱波段的局部相关性，提出另一种特征分组方法。

光谱Wiener滤波矩阵A定义为

式中：Σ是高光谱数据的协方差矩阵。

第i波段光谱Wiener滤波估计误差可表示为

同方程（18）定义的相关系数相比，与线性光谱估计误差有关的局部相关系数定义为

相应的局部相关系数矩阵可以写为

Indian Pine高光谱数据的局部相关系数如图2所示。通过测量一组连续波段间的局部相关性，利用预设阈值来调制子空间边界。例如，如果pi，i+1高于预设阈值，波段yi+1被认为是属于yi子空间的元素；否则，波段yi+1属于下一个子空间。分组过程重复从第1对波段到最后1对。

2.3.3 基于互信息的子空间

前面提过的相关系数与局部相关系数都可以表示2个变量的线性关系。在信息论中，互信息（MI）可以作为另一种方法来度量2个随机变量的统计独立性。

假设高光谱图像的2个波段为2个离散变量A和B。A和B的互信息定义如下：

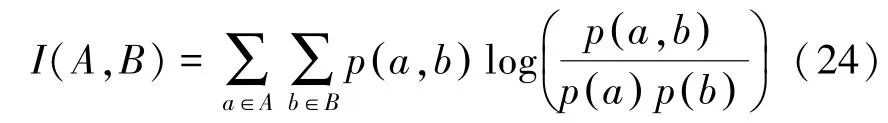
式中：p( a)和p( b)是A和B的边缘概率分布，表示光谱波段反射值得分布，p( a，b)是A和B的联合概率密度分布。

互信息矩阵MI由每2个光谱波段的互信息计算得到，根据方程（24）来定义，Iij＝I( yi，yj)，MI表示为

互信息矩阵也可以由一个二维图像显示出来，这样可以提供一个全局的视觉评价。Indian Pine高光谱数据的MI图像如图3所示。图3表明高光谱数据的互信息矩阵具有分块的性质，即相邻光谱波段有很强的相关性。所以MI可以作为一种波段分组的依据，如前文描述的相关系数一样。

与基于相关性的分组方法相似，基于MI的分组方法通过控制预设阈值逐步扩大和划分子空间。具体的过程与基于相关性的方法相同，只需要用互信息代替相关系数，并改变相应的阈值。

2.4 确定调制向量

对于高光谱图像分类，在SM-KPCA方法中，由地物真实图得到的先验类别信息用于确定优化子空间的调制向量ΔS。光谱波段图像与已知的地物真实图间的互信息可以显示该波段的类别可分性，并能度量出对分类的贡献。根据方程（24）计算互信息，这里的2个变量将由地物真实图和波段图像所代替。因此，在已知先验信息的监督方法下，子空间数据的光谱波段与地物真实图间的互信息用于确定子空间调制向量ΔS。其应用过程按如下实现：首先，计算每个波段与地物真实图的互信息，然后采用同一子空间下所有波段的平均互信息作为子空间调制权值σsh( h＝1，2，…，M)。

3 实验与结果分析

为了验证该算法的有效性，对真实高光谱数据进行数值实验。本文用地表覆盖物的分类来客观地评价和比较本文的SM-KPCA方法与传统的KPCA方法。另一个用于比较的方法是SWK，它需要确定全局空间调制向量ΔW，由SWKPCA定义得到SWK PCA。在客观评价中，分类方法采用的是一对一的SVM多类分类方法。

在实验中，本文提出的SM-KPCA方法对高光谱数据进行特征提取，数据为AVIRIS在西北印第安纳的印第安平原采集得到的。原始数据包括224个光谱波段，每个波段图像是145×145像素。去掉4个全为零的波段和20个受大气水分吸收影响的波段，使用200个波段用于实验。在使用SM-KPCA方法之后，对所有16类地物进行基于SVM的监督分类，利用真实地物图对特征提取的表现进行评价。在分类过程中，16类样本中每一类的20%用于训练，余下的80%用于测试。

对于不同方法其实验的设置如下。

3.1 不同特征分组

实验中采用第4部分描述的3种特征分组方法，相应的阈值用于控制子空间边界，如表1所示。为了更加清楚地比较不同方法，通过调整阈值来得到一些特定的子空间数目，本实验中设置为10、15、20和25。表1表明阈值是随着子空间数目增加而增加的。这种趋势与只有相邻波段间存在高相关性的现象一致。

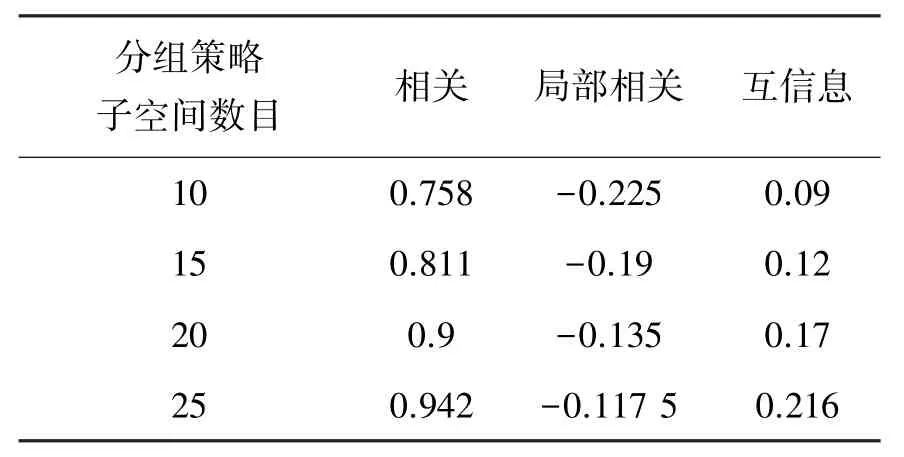
表1 不同子空间分组方法的阈值Table 1 Threshold of different subspace grouping

3.2 比较先验方法下通过不同子空间方法提取的特征

在先验调制方法下提出的SM-KPCA方法执行了第4部分介绍的3种特征分组方法。高斯径向基函数作为核函数和特征加权核的原型，带宽参数σ设为1。由传统KPCA、SWKPCA和SM-KPCA提取的前5个特征如图1、2和3所示，其中，子空间的数目设为20。

图1 传统KPCA方法提取的前5个特征Fig.1 First five features by KPCA

图2 SW-KCPA方法提取的前5个特征Fig.2 First five features by SW-KPCA

图3 不同SM-KPCA算法提取的前5个特征Fig.3 First five features by SM-KPCA

3.3 分类性能

分类中，采用基于SVM，SVM-KM分类的MATLAB工具箱和高斯径向基函数。分类是在不同数量（5～25）的主成分数目上进行的，图4分别给出总体分类精度曲线（表1列出不同子空间数目）。可以看出，子空间调制核PCA可以极大地改善核PCA的分类性能。与光谱加权核PCA相比，本文的SMKPCA在多数情况下更有效。在这3种特征分组方法中，没有哪一种完全好于其他方法。但是可以找到一种方法，它在利用基于分组的互信息方法的多数情况下性能更优越。此外，在考虑一些非线性成分时基于相关性的分组方法SWKPCA也显示出很好的性能。

图4 总体分类精度Fig.4 Overall accuracy of classification

子空间的数目影响着SM-KPCA的性能，所以在实验中分析了这种影响，相应的结果如图5所示。同时考虑SW-KPCA，因为它可以视为一种特殊的情况，即有200个调制子空间。从这一点可以得出结论，本文的子空间调制核方法好于光谱加权核的方法。图5中，当子空间的数目从15变化到25时，SM-KPCA方法要好于其他方法，这表明子空间的数目不能过大或过小。

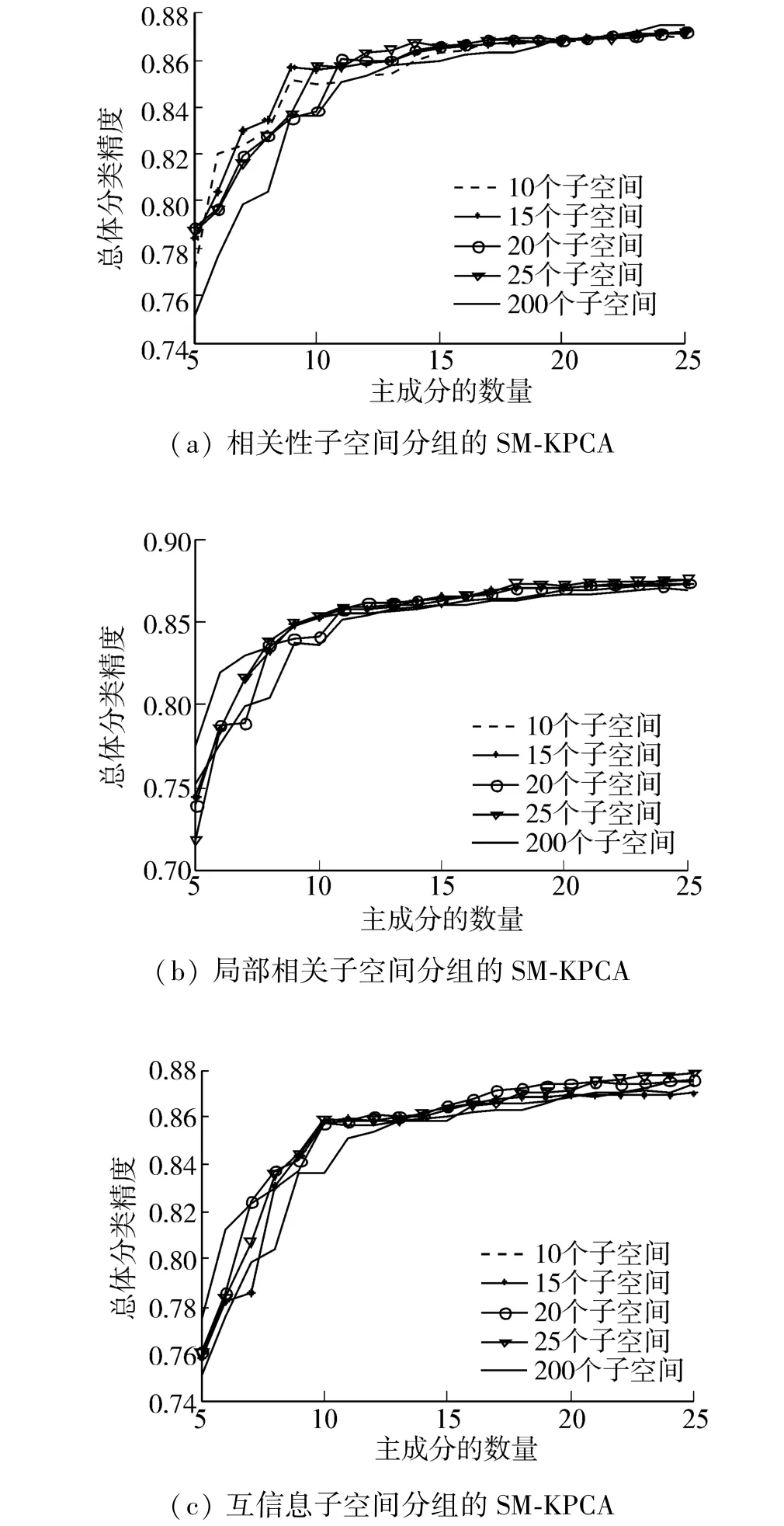
图5 不同子空间数量下的总体分类精度Fig.5 Overall accuracy with different number of subspaces

4 结论

本文提出一种新颖的子空间调制核方法用于高光谱图像降维后的分类。在低维特征上的分类用于客观的评价方法的特征提取性能。在本文提出的方法中，高光谱图像的特征加权核与特征分组特性整合到了传统的核方法中，并用于提高数据的适应性，且得到了SM-KPCA方法。与传统KPCA与SWK方法相比，针对降维后的分类处理效果和性能来说，SMK方法更有效。

本文提出的方法中，分类作为一个目的用来引导和评价子空间调制核结构。所以，未来的工作是如何扩展其他的调制核结构的应用领域，通过更有效的集成核方法与高光谱图像的空谱结构信息使得在高光谱图像的多种重要应用中得到最优处理效果，例如光谱解混、目标检测。

［1］VANE G，GREEN R O，CHRIEN T G，et al.The airborne visible／infrared imaging spectrometer（AVIRIS）［J］.Remote Sens Environ，1993，44：127-143.

［2］LANDGREBE D.Hyperspectral image data analysis as a high dimensional signal processing problem［J］.IEEE Signal Process Mag，2002，19（1）：17-28.

［3］林娜，杨武年，王斌.高光谱遥感影像核最小噪声分离变换特征提取［J］.武汉大学学报：信息科学版，2013，38（8）：988-992.

LIN Na，YANG Wunian，WANG Bin.Hyperspectral image feature extraction via kernel minimum noise fraction transform［J］.Geomatics and Information Science of Wuhan University，2013，38（8）：988-992.

［4］杜培军，王小美，谭琨，等.利用流形学习进行高光谱遥感影像的降维与特征提取［J］.武汉大学学报：信息科学版，2011，36（2）：148-152.

DU Peijun，WANG Xiaomei，TAN Kun，et al.Dimensionality reduction and feature extraction from hyperspectral remote sensing imagery based on manifold learning［J］.Geomatics and Information Science of Wuhan University，2011，36（2）：148-152.

［5］JIA X，RICHARDS J A.Segmented principal components transformation for efficient hyperspectral remote-sensing Image display and classification［J］.IEEE Trans Geosci Remote Sens，1999，37（1）：538-542.

［6］CAMPS-VALLS G，GOMEZ-CHOVA L，MUNOZ-MARI J，et al.Composite kernels for hyperspectral image classification［J］.IEEE Geosci Remote Sens Lett，2006，3（1）：93-97.

［7］GU Y，LIU Y，ZHANG Y.A soft classification algorithm based on spectral-spatial kernels in hyperspectral images［C］／／Second International Conference on Innovative Computing，Information and Control，ICICIC 2007.Kumamoto，Japan，2007：1-4

［8］FAUVELE M，CHANUSSOT J，BENEDIKTSSON J A.A-daptive pixel neighborhood definition for the classification of hyperspectral images with support vector machines and composite kernel［C］／／IEEE International Conference on Image Processing，ICIP’08.San Diego，USA，2008：1884-1887.

［9］TUIA D，RATLE F，POZDNOUKHOV A，et al.Multisource composite kernels for urban-image classification［J］.IEEE Geosci Remote Sens Lett，2010，7（1）：88-92

［10］CAMPS-VALLS G，MARSHEVA T V B，ZHOU D.Semisupervised graph-based hyperspectral image classification［J］.IEEE Trans Geosci Remote Sens，2007，45（10）：3044-3054.

［11］CAPOBIANCO L，GARZELLI A，CAMPS-VALLS G.Target detection with semisupervised kernel orthogonal subspace projection［J］.IEEE Trans Geosci Remote Sens，2009，47（11）：3822-3833.

［12］MARCONCINI M，CAMPS-VALLS G，BRUZZONE L.A composite semisupervised SVM for classification of hyperspectral images［J］.IEEE Geosci Remote Sens Lett，2009，6（2）：234-238.

［13］GUO B，GUNN S R，DAMPER R I，et al.Customizing kernelfunctions for svm-based hyperspectralimage classification［J］.IEEE Trans Image Process，2008，17（4）：622-629.

［14］MANOLAKIS D，LOCKWOOD R，COOLEY T.On the spectral correlation structure of hyperspectral imaging data［C］／／IEEE International Geosience and Remote Sensing Symposium，IGARSS’08.Cape Town，South Africa，2008：581-584.

A subspace kernel learning method for feature extraction of the hyperspectral image

LIU Zhenlin，GU Yanfeng，ZHANG Ye
（School of Electronics and Information Engineering，Harbin Institute of Technology，Harbin 150001，China）

Feature extraction is quite valuable for the mining and utilization of valid information in hyperspectral remote-sensing imaging and the increase of subsequent classified applications.For improving the dimension reduction effect，a subspace-modulated kernel principal component analysis（SM-KPCA）method is proposed.With this method，the grouping natures of hyperspectral data are integrated into a uniform kernel method framework and a subspace-modulated kernel is constructed.SMK（subspace-modulated kernel）achieves a sparse modulation on the spectral waveband by means of feature grouping；in addition，it is a data-adaptive kernel for measuring the nonlinear similarities among the hyperspectral data specimens.With the proposed method，AVIRIS（airborne visible infrared imaging spectrometer）real hyperspectral imaging is applied for evaluation.Additionally，this method is compared with the conventional kernel method and the spectrally weighted kernel method.The experimental results show that the SM-KPCA method more sufficiently utilizes the complex and relevant physical characteristics between wavebands.Therefore，itoutperforms both the conventional kernelmethods and the spectrally weighted kernelmethod regarding the aspect of the classification of hyperspectral images.

hyperspectral images；kernel methods；data dimension reduction；image classification；feature extraction

10.3969／j.issn.1006-7043.201309025

TN911.73

A

1006-7043（2014）02-0238-07

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006-7043.201309025.html

2013-09-06.网络出版时间：2014-1-2 15：26：13.

国家自然科学基金资助项目（61371180）.

刘振林（1970-），男，博士研究生；

谷延锋（1977-），男，教授，博士生导师.

谷延锋，E-mail：guyf＠hit.edu.cn.