基于参数化小波的主冷却剂泵故障特征识别

李 彬，夏 虹

（哈尔滨工程大学核安全与仿真技术国防重点学科实验室，黑龙江哈尔滨150001）

基于参数化小波的主冷却剂泵故障特征识别

李 彬，夏 虹

（哈尔滨工程大学核安全与仿真技术国防重点学科实验室，黑龙江哈尔滨150001）

针对核反应堆冷却剂泵在经过长期运行之后，转子可能出现的裂纹故障，利用小波分析技术，能够实现对这些故障特征的识别。在研究中，不同于以往的直接利用现有小波分析信号特征，而是从小波滤波器的角度出发，利用紧支撑正交小波的二尺度方程及尺度系数和小波系数的特点，结合滤波器的多相表示以及无损FIR滤波器的矩阵计算方法，对小波滤波器系数进行了参数化。通过选取不同的序列长度和消失矩，计算得到一系列小波滤波器系数。最后取其中一组参数化小波以及具有相同消失矩的db小波分别对反应堆主冷却剂泵的振动仿真信号进行分析，结果显示该参数化小波可以清晰准确地识别出转子的裂纹故障特征。

反应堆冷却剂泵；裂纹故障；参数化小波；特征识别；转子裂纹；小波滤波器；小波分析

核反应堆冷却剂泵的安全运行直接关系核电厂的安全，所以对冷却剂泵运行状态的监测是必要的。国内外核电厂中，反应堆冷却剂泵的常见故障主要有动不平衡、轴裂、主轴损坏等［1］，虽然转子裂纹故障几乎很少出现，但是作为一个大型的旋转机械设备，该故障仍然存在出现的可能性，一旦不能及时准确的发现裂纹并进行处理，将对反应堆冷却剂泵以及核电厂的安全运行埋下隐患，所以有必要对其进行故障特征分析、识别。当转子出现裂纹故障时，其振动信号会出现比较明显的频率特征，而对于振动信号的故障特征识别至今已有多种方法［2-4］。在这些方法中，小波分析技术已经成为比较成熟的技术，并且，相对于常用的傅氏变换，小波变换能更好地处理非线性非平稳信号，能及时实现信号的时频分析，并对现有的反应堆冷却剂泵振动监测系统起到补充完善的作用。目前在工程应用中，多数采用离散的db小波或者haar小波，也有少部分利用连续的morlet小波［5］。然而，不同的小波具有不同的性质，对信号的分析能力也不同，对同一信号采用不同的小波所得到的分析结果也相差很大［6-7］。小波分析的过程其实是利用小波滤波器与信号进行卷积的过程，而紧支撑正交小波的滤波器其实是一组正交镜像滤波器，P.P.Vaidyanathan曾对这种数字滤波器进行详细研究［8］，Hehong Zou与Ahmed H.Tewfik等在前者的基础上计算出了当消失矩为1时的haar小波的参数方程［9］。此后，D.Bharath Bhushan等又利用不同的方法对haar小波进行了参数化研究［10］。

本文基于紧支撑正交小波的滤波器特点，深入研究了小波滤波器的参数化方法，通过计算不仅得到了haar小波的参数方程，同时也计算出了消失矩大于1时的小波参数方程，并发现当消失矩为N时，除已存在的dbN小波外，仍然存在其他与之具有相同消失矩的小波。同时，结合反应堆冷却剂泵转子裂纹振动仿真信号，验证该方法计算出来的小波是否具有工程实用性。

1 小波滤波器的多相表示

正交小波的二尺度方程如下：

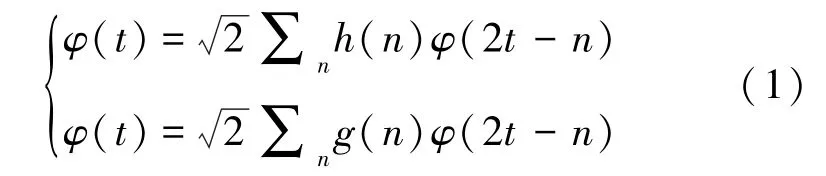
其中，展开系数h（n）和g（n）分别称为尺度系数与小波系数，它们对应的滤波器就是低通和高通滤波器，尺度系数h（n）与小波系数g（n）必须满足如下条件：

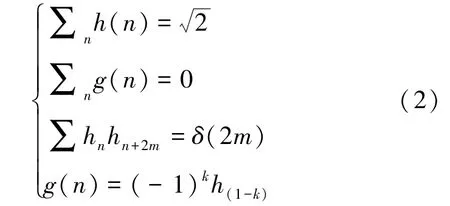
这样，才能得到能够完全重构信号的正交滤波器序列，除此之外，h（n）还应满足正则性条件：

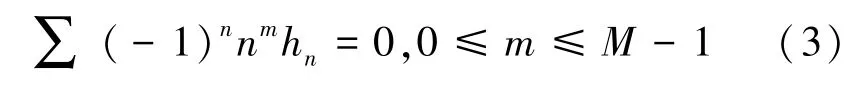
其中，M为消失矩阶数，即存在H（M）（z）|z＝-1＝0，即H（z）的M阶以下导数在z＝-1处都为零。M越大，则尺度函数越光滑，但是同时小波函数的支撑长度也越大。

小波滤波器的多相矩阵表示如下［9］：

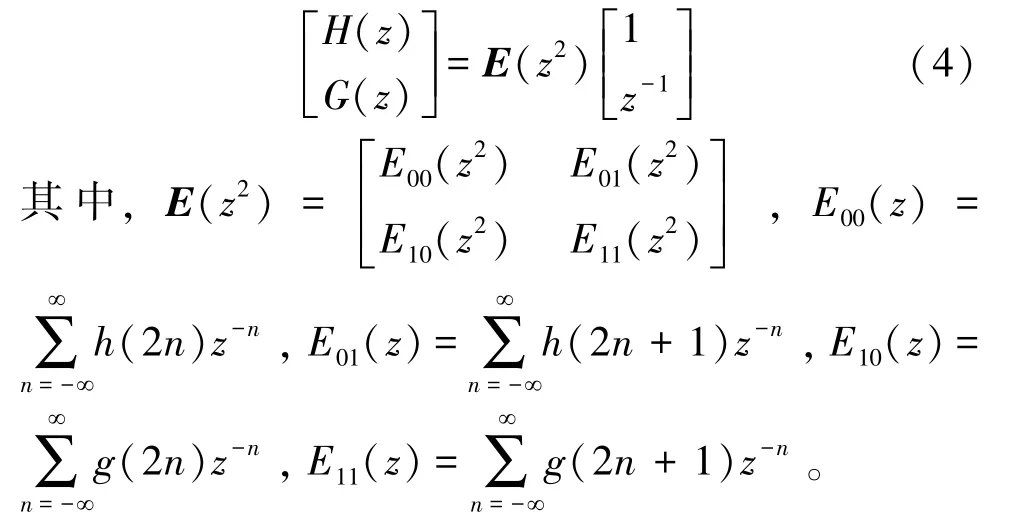
2 小波滤波器系数参数化方法

取滤波器序列h（n）的长度为2 N（其长度只能为偶数［11］），对于一个2×2的因果FIR滤波器无损矩阵，E（z）可以表示为［12］

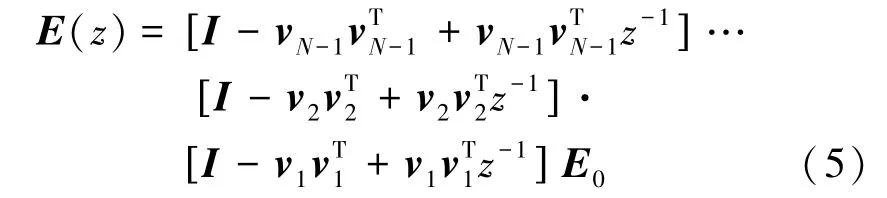
其中，E0是N＝1时滤波器系数的多相矩阵，且是一个2×2的常数酉矩阵，vk是2×1的实系数列向量，并且有＝I，不妨设

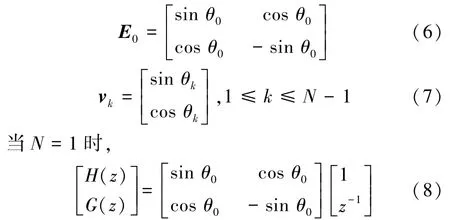
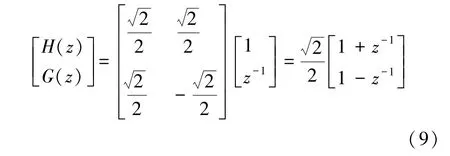
经过z反变换可以得出

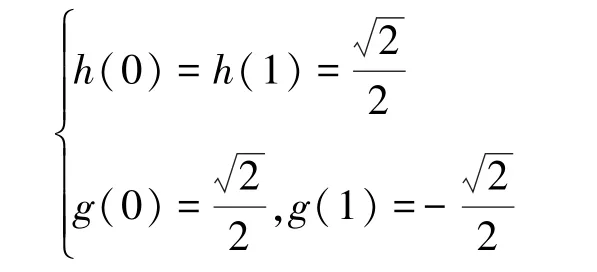
此时得出的滤波器系数正是haar小波的滤波器冲击响应，当N＝2时，由式（4）和（5）可以得到

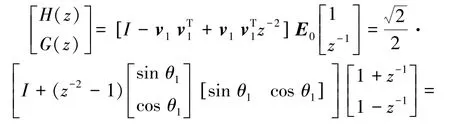
当小波函数具有二阶消失矩时，有H（z）的一阶导数在z＝-1处含有一个零点，此时得到4cosθ sinθ＝1，可以解出在0～2π内θ＝或111者θ＝，结合式（14）可以计算出当θ＝时，11h（0）＝0.482 962 913 144 534，h（1）＝0.836 516 303 737 808，h（2）＝0.224 143 868 042 013，h（3）＝-0.129 409 522 551 260。

该滤波器系数h（n）就是db2小波的尺度系数［13］。当N＝3时，结合多相矩阵可以得到滤波器h（n）的系数表达式：

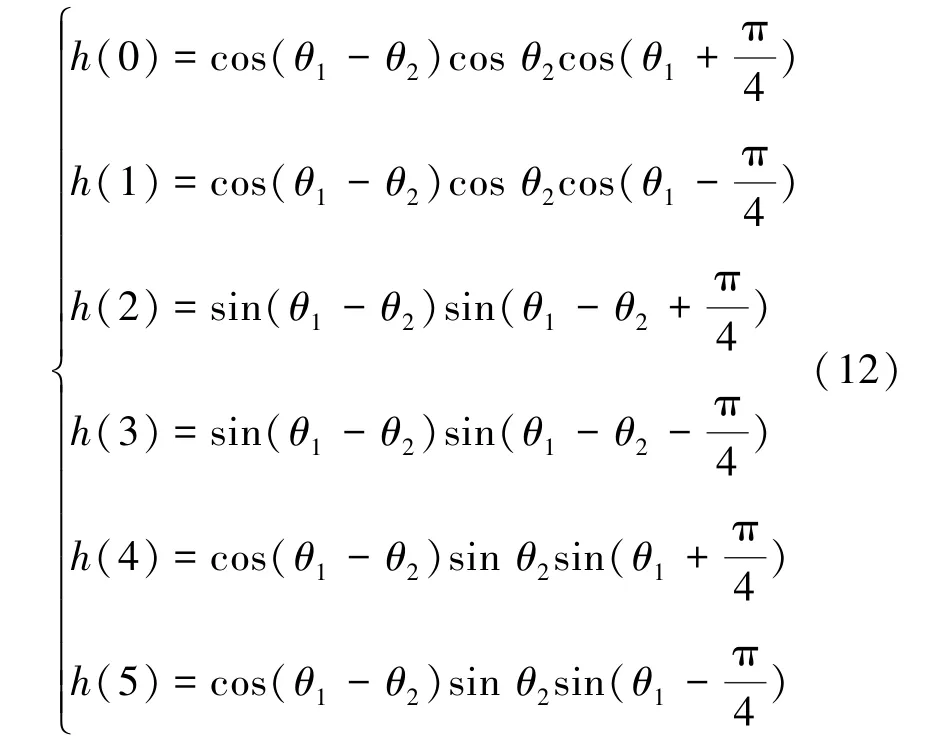
当小波函数具有三阶消失矩时，有H（z）的一阶和二阶导数分别在z＝-1处含有一个零点，可以得到

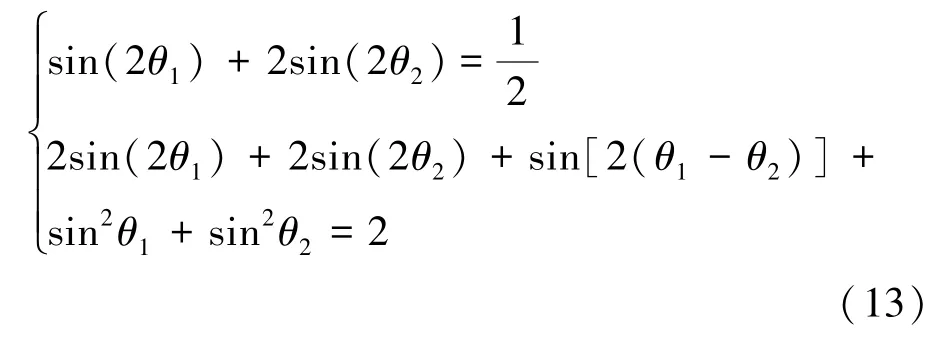
此时，在0～2π范围内可解出θ11＝0.394 344 971 025 249，θ12＝1.176 451 355 769 647，θ21＝ 6.177 689 010 003 046，θ22＝4.817 885 277 561 225。

其中，θ1与θ2的2组值可组成4组解，即有4个符合条件的小波，经过验证计算，发现由（θ11，θ21）构成的解所求出的滤波器系数正好是db3小波的尺度系数，而其他3组解则是符合条件但尚未被应用的小波。类似地，当N＞3时，由式（7）结合适当的消失矩阶数可以计算出不同参数θk下的滤波器系数，实现了小波的参数化方法，并且发现除包含dbN小波外，仍然存在其他符合条件的尚未命名的小波。然而这些小波是否具有较好的信号分析能力，本文将利用其中的参数化小波来分析核反应堆冷却剂泵的振动仿真信号，分析识别裂纹转子的故障特征，以此说明该方法计算出的小波在反应堆冷却剂泵故障诊断方面的应用价值。

3 反应堆主冷却剂泵转子裂纹故障特征识别

3.1 反应堆冷却剂泵结构

反应堆冷却剂泵是屏蔽电机泵，其结构如图1所示。

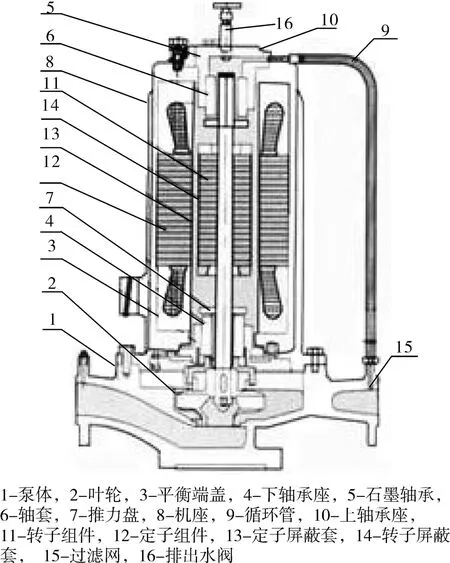
图1 反应堆冷却剂泵结构示意图Fig.1 Schematic diagram of RCP

电动机转子和泵的叶轮构成一个整体转子，电动机的转子与定子之间用屏蔽套隔开，下端相当于一般工业用的悬臂式单级泵。叶轮上方设有隔热屏，起热屏蔽作用，防止冷却剂的热量向电动机方向传导。电动机的定子转子及叶轮全部封闭在高压壳体内。高压壳体外部盘绕螺旋管热交换器。螺旋管外部通流二次冷却水，一次冷却水与一回路冷却剂相通，所以螺旋管内的压强就是一回路压强。一次冷却水从泵的上方进入辅助叶轮，从辅助叶轮流出后，沿定子与转子的间隙向下流动，同时将定子与转子的热量带走，并润滑下部径向轴承和推力轴承，再流到螺旋管，由下而上由螺旋管流回顶部，构成一次冷却水循环。低压二次冷却水从泵中间向下流，冷却螺旋管后，从下部出口流出，构成二次冷却水循环，实现热交换［14］。

3.2 反应堆冷却剂泵裂纹转子振动模型

一般情况下，核电厂安装有反应堆冷却剂泵振动监测系统，通过利用每台泵上安装的2个加速度传感器实时监测振动状态。由于条件所限，无法获取反应堆冷却剂泵的实际故障振动信号，尤其是转子裂纹故障信号。为此，本文结合反应堆冷却剂泵的结构特点建立了力学振动模型对裂纹故障进行仿真模拟研究。

反应堆冷却剂泵一般情况下是垂直安装，所以要充分考虑轴承和基础对转子的影响，基于此，研究中建立了垂直安装主泵的裂纹转子-轴承-基础的振动模型，如图2所示。

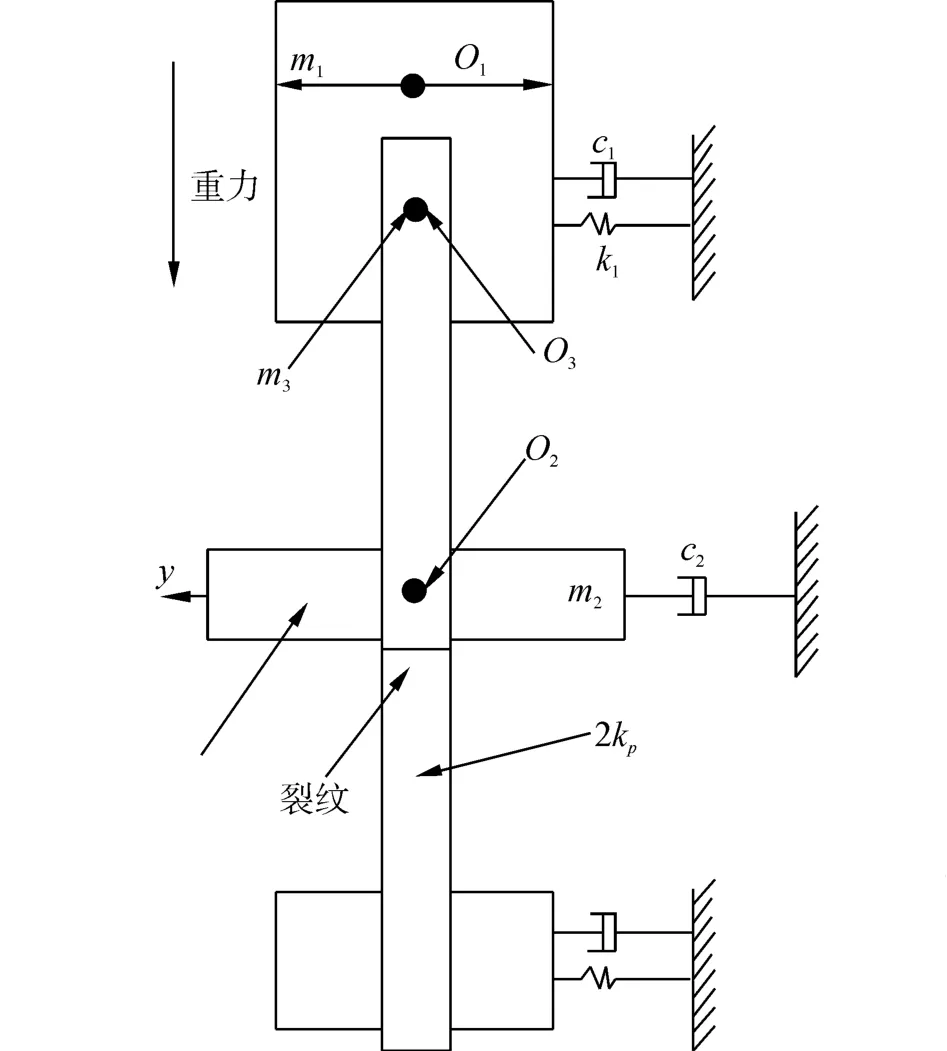
图2 反应堆冷却剂泵裂纹转子模型Fig.2 Model of the cracked rotor of RCP

图2中m1为泵体等效质量；O1为m1的质心；c1为泵体支撑阻尼；k1为泵体支撑刚度；m3为轴等效质量；O3为m3的质心；m2为等效圆盘质量；Oe为等效圆盘质心；y表示径向；O2为轴心；c2为转子阻尼；2 kp为转轴刚度。该模型的振动微分方程如式（14）所示，式中x、y为各个等效质量的径向振幅；c、k分别为阻尼和刚度；e为等效圆盘的偏心距；m为各个等效质量；w为轴转速；t为时间；φ为初始相位角.

裂纹转子的刚度表示如式（15）所示。

在式（15）和（16）中，θ＝wt+φ+β-φ，其中φ可由tanφ＝得到，β为转子偏心方向与裂纹方向的夹角，α可以通过cosα＝求出，R、T分别为轴直径和裂纹深度，k0为无裂纹时的初始刚度，Δkη、Δkξ为有裂纹时的刚度变量。

3.3 反应堆冷却剂泵裂纹特征识别

由于常见的故障特征具有明显的频率特性，例如，转子出现裂纹时，会使转轴的刚度不对称，引起非线性振动，其旋转频率的2倍频、3倍频等高频分量将会出现。由于反应堆冷却剂泵转子裂纹故障特征只与旋转频率有关，与其他参数，如转子质量、刚度等无关，所以在该研究中，通过查阅与反应堆冷却剂泵类似的屏蔽泵的一些参数来设置仿真模型的参数，虽然其与实际泵的参数有差别，但是其频率特征是固定的，由于本文需要验证的是利用参数化方法计算出来的小波能否识别出这些特征频率以及实际效果。所以，并不会影响对识别方法有效性的判断。

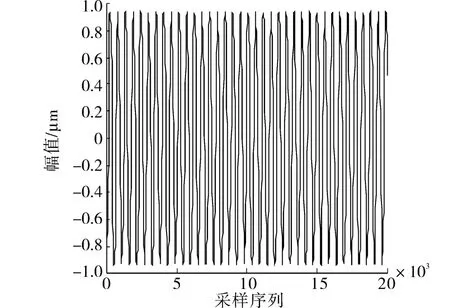
图3 振动仿真信号Fig.3 Vibration simulation signal

现设转轴转速w＝2 200 r／min，m1＝200 kg，m2＝220 kg，m3＝30 kg，c1＝4 300 N·s／m，c2＝9 300 N·s／m，c3＝3 000 N·s／m，k1＝5.26×107N／m，2kp＝k2＝2.104×108N／m，k3＝5×107N／m，e＝0.2 mm，φ＝0，α＝π，β＝0，这里裂纹取在ξ方6向上，kη＝2.004×108N／m，kξ＝1.8×108N／m.其仿真信号如图3所示，其中采样频率为2 000 Hz.

接下来利用参数化方法计算出来的小波来分析信号的频率成分。这里，不妨取N＝3时，同时具有三阶消失距情况下的θk值（θ11，θ22），由此可以求出小波的尺度系数：h（0）＝-0.011 432 880 447 242，h（1）＝-0.027 730 420 014 761，h（2）＝0.456 658 729 352 313，h（3）＝0.842 807 199 080 631，h（4）＝0.261 880 932 281 477，h（5）＝-0.107 969 997 879 323。

用该小波对仿真信号进行5层小波包分解，由于小波包分析自身存在频率混淆等问题，因此，结合频率补偿法［15］对仿真信号进行分析，各节点的真实频率成分以及排序如图4（a）所示。同时，取N＝3时的Daubechie系列小波db3也对信号进行小波包分析，如图4（b）所示。

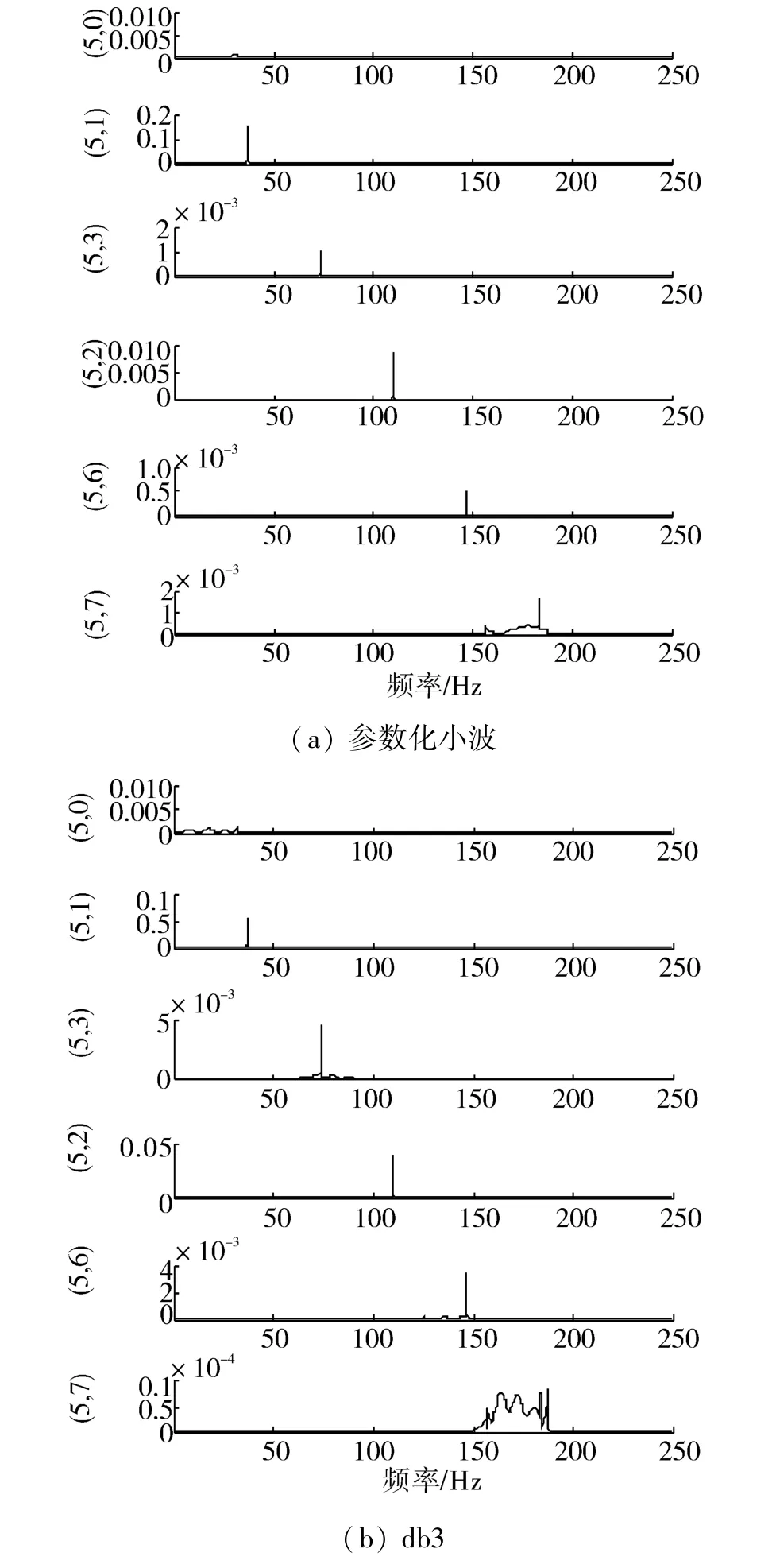
图4 仿真信号的小波包分析结果Fig.4 WPT result of the simulation signal

从图4中分析结果可以看出，在小波包节点（5，0）处，2种小波都清晰地分析出了转子的旋转频率36.7Hz，除此之外，在节点（5，3）、（5，2）以及（5，6）上分别存在旋转频率的2倍频、3倍频和4倍频分量，但是，对比2种小波的分析结果可以发现，相对于db3小波，参数化小波具有较小的幅值失真。仿真结果表明，利用小波参数化方法计算出的小波能够很好地识别出反应堆冷却剂泵转子出现裂纹时的频率故障特征，并且具有较小的幅值失真。

4 结束语

本文对小波的参数化计算方法进行了研究，构造出了满足紧支撑正交条件的其他小波，并且发现dbN系列小波是该方法计算出来的特例。利用该方法构造的小波以及db3小波对反应堆主冷却剂泵的振动仿真信号分别进行了小波包分析，结果表明，相对于常用的小波基，参数化小波不仅能够清晰准确地识别出主泵转子出现裂纹时的高频故障频率，而且具有较小的幅值失真。

由于条件所限，本文工作是基于所建的主泵转子力学模型来对裂纹振动信号进行仿真和故障特征识别的，因此，在实际工程应用时，还需要结合实际信号对方法进行适当的修改完善，并结合已有的监测方法对反应堆冷却剂泵进行在线监测。

［1］周晓宁.核反应堆冷却剂泵主循环泵常见故障分析［J］.设备管理与维修，2012（2）：33-35.

ZHOU Xiaoning.Analysis of the common faults of the main circulating pump of the RCP［J］.Plant Maintenance Engineering，2012（2）：33-35.

［2］谢长贵，谢志江.模糊Kohonen神经网络的旋转机械故障诊断［J］.现代科学仪器，2012，5：95-98.

XIE Changgui，XIE Zhijiang.Fuzzy fault diagnosis for rotating machinery based on Kohonen neural network［J］.Modern Scientific Instruments，2012，5：95-98.

［3］李志农，蒋静，赵匡，等.基于Volterra级数和SVM的旋转机械故障诊断方法研究［J］.机械强度，2012，34（5）：633-637.

LI Zhinong，JIANG Jing，ZHAO Kuang，et al.Fault diagnosis method of rotating machinery based on Volterra series and SVM［J］.Journal of Mechanical Strength，2012，34（5）：633-637.

［4］周洋.小波分析在旋转机械振动信号监测和故障诊断中的应用研究［D］.上海：同济大学，2007：45-48.

ZHOU Yang.Research on application of wavelet in the rotating machinery fault diagnosis［D］.Shanghai：Tongji University，2007：45-48.

［5］SCHUKIN E L，ZAMARAEV R U，SCHUKIN L I.The optimization of wavelet transform for the impulsive analysis in vibration signals［J］.Systems and Signal Processing，2004，18（6）：1315-1333.

［6］孔国杰，张培林，徐龙堂，等.信号奇异性检测中的小波基选择及其工程应用［J］.机械科学与技术，2009，28（4）：542-545.

KONG Guojie，ZHANG Peilin，XU Longtang，et al.Selection of waveletbase in signalsingularity detection and its application［J］.Mechanical Science and Technology for Aerospace Engineering，2009，28（4）：542-545.

［7］田幕玲，王晓玲.电机故障诊断中的小波分析方法及小波基选取［J］.煤矿机械，2007，28（5）：176-178.

TIAN Muling，WANG Xiaoling.Wavelet analysis method applied in fault diagnosis of motor and selection of wavelet base［J］.Coal Mine Machinery，2007，28（5）：176-178.

［8］VAIDYANATHAN P P.Multirate digital filters，filter banks，polyphase networks，and applications：a tutorial［J］.Proc IEEE，1990；78（1）：56-93.

［9］ZOU Hehong，TEWFIK A H.Parametrization of compactly supported orthonormal wavelets［J］.IEEE Trans on Signal Processing，1993，41（3）：1428-1531.

［10］BHUSHAN D B，SOMAN K P.Polyphase matrix factorization—a simplified explanation［C］／／2009 International Conference on Advances in Recent Technologies in Communication and Computing.［S.l.］，2009.

［11］DAUBECHIES I.Orthonormal bases of compactly supported wavelets：commun［J］.Pure Appl Math，1988，41：909-996

［12］VAIDYANATHAN P P，DOGANATA Z.The role of lossless systems in modern digital signal processing：a tutorial［J］.IEEE Trans on Education，1989，32（3）：181-197.

［13］李登峰，杨晓慧.小波基础理论和应用实例［M］.北京：高等教育出版社，2010：70-71.

［14］高璞珍.核动力装置用泵［M］.哈尔滨：哈尔滨工程大学出版社，2004：98-100.

［15］夏虹，黄华，陈志辉.基于频率补偿小波的屏蔽主泵裂纹转子识别［J］.原子能科学技术，2010，44（7）：841-847.

XIA Hong，HUANG Hua，CHEN Zhihui.Identification of cracked rotor of canned motor pump based on wavelet analysis of frequency compensation［J］.Atomic Energy Science and Technology，2010，44（7）：841-847.

Feature recognition of the RCP fault based on the parameterized wavelet

LI Bin，XIA Hong
（Fundamental Science on Nuclear Safety and Simulation Technology Laboratory，Harbin Engineering University，Harbin 150001，China）

Focusing on the possibility ofa crack faultappearing in a rotor after the reactor coolantpump（RCP）has operated for a long time，the waveletanalysis technology may be utilized for the identification of these faultfeatures.This research offered a differentmethod from the previous way of analyzing the signalfeature by directly utilizing the existing wavelet，from the viewpoint of the wavelet filter，by utilizing the characteristics of the two-scale equation compactly supported orthogonal wavelet，the scale coefficients and the wavelet coefficients，in combination with the polyphase expression ofthe filters and the matrix calculation method of the lossless FIR filters，the wavelet filter coefficients are parameterized.A series of wavelet filter coefficients are calculated by choosing different sequential lengths and vanishing moments.Finally，the vibration simulation signal of the RCP is analyzed respectively by applying a group of parameterized wavelets and the db wavelets which have the same vanishing moment.The results show that the fault feature of a rotor crack may be identified clearly and accurately by the parameterized wavelets.

reactor coolant pump；crack fault；feature recognition；parameterized wavelet；rotor crack；wavelet filter；wavelet analysis

10.3969／j.issn.1006-7043.201212101

TL37

A

1006-7043（2014）02-0261-06

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006-7043.201212101.html

2012-12-26.网络出版时间：2014-1-2 14：56：02.

国家自然科学基金资助项目（51379046）.

李彬（1984-），男，博士研究生；

夏虹（1962-），女，教授，博士生导师.

夏虹，E-mail：xiahong＠hrbeu.edu.cn.