改进的模糊综合评价法在同里古镇水质评价中的应用

徐 健吴 玮黄天寅贾海峰

(1.苏州科技学院环境科学与工程学院,江苏苏州 215009;2.清华大学环境科学与工程系,北京 100084)

改进的模糊综合评价法在同里古镇水质评价中的应用

徐 健1,吴 玮1,黄天寅1,贾海峰2

(1.苏州科技学院环境科学与工程学院,江苏苏州 215009;2.清华大学环境科学与工程系,北京 100084)

根据2012年3—8月同里古镇8个监测断面水质的监测结果,应用改进的模糊综合评价法,采用6级隶属函数与熵权,通过最大隶属度原则的有效度及置信度准则判定同里古镇水质类别,并与采用传统的模糊综合评价法所得的水质评价结果进行对比。结果表明:同里古镇水质状况较差,内部水质为Ⅴ类或劣Ⅴ类,外部水质相对较好;与传统的模糊综合评价法相比,改进的模糊综合评价法更具区分度,能评价劣Ⅴ类水质,且权重计算简单,能确定主要污染因子,评价结果更为合理可靠。

水质评价;改进的模糊综合评价法;6级隶属函数;熵权;置信度准则;同里古镇

水环境因子和人类健康的关系存在模糊性,且污染程度也是一个模糊概念,因此,水环境质量分级本身就具有模糊特征[1]。基于模糊矩阵和隶属度概念的模糊综合评价是一种应用广泛的水质评价方法[2-3]。利用模糊综合评价法评价水质,就是找出影响水质的主要因素,确定评价因子集、评价集、隶属函数,然后通过计算各因素的隶属度和权重,得到综合隶属度,最后确定水质类别[4]。

传统的模糊综合评价法一般以水质标准的上下限为界限值代入隶属函数,从而得到水质因子相对于Ⅰ～Ⅴ类的隶属度,但是这样造成的结果是将劣Ⅴ类的水质也归为Ⅴ类,无法满足对劣Ⅴ类水质的评价。基于上述原因,徐兵兵等[5]提出以水质标准上下限的中间值作为隶属函数的界限值,从而得到6个隶属度,以克服传统的模糊综合评价法的不足。

各评价因素的权重确定是模糊综合评价模型的核心问题。权重的确定方法通常有单项评价指标权重法、综合权重法及熵权法,王涛等[6]对此进行了比对研究,发现熵权法能够较全面地反映水质实际情况。信息熵的概念由信息论之父Shannon于1948年提出,如今已在社会科学和自然科学的多个领域得到了充分的研究与应用[7-9]。Mogheir等[10]应用熵理论对加沙地带的地下水质监测网络进行了评估与重新设计,减少了多余的信息,降低了监测的成本;孟宪萌等[11]在集对分析模型中应用熵值赋权得出科学而合理的结果。

水质类别是通过各断面水质综合隶属度来确定的。传统的模糊综合评价法利用最大隶属度原则来确定水质类别,但由于模糊数学本身的缺陷性,特别是当各水质指标的所属水质类别同步性较差时,进行水质评价的最大隶属度原则往往失效,出现评价结果失真、均化和跳跃等现象[12]。针对模糊数学中最大隶属度原则的适用性,郭东星等[13]提出了最大隶属度原则有效度概念,若最大隶属度原则被判断为失效,则需引进另外的评价原则。程乾生[14]在属性识别理论模型中提出置信度准则,并成功应用于大气环境质量评价中。贺玉龙等[15]采用置信度准则对2005年涪江水质进行模糊综合评价,得到合理、可靠的结果。

笔者采用基于6级隶属函数、熵权和水质类别判定原则的改进模糊综合评价法,对同里古镇水质进行评价,并通过实例来对比分析改进的模糊综合评价法和传统的模糊综合评价法的评价结果。

1 评价方法

鉴于本文主要讨论模糊综合评价中的隶属度计算、熵值赋权以及水质类别判定原则,而在评价步骤上,改进的模糊综合评价法与传统的模糊综合评价法类似,因此,关于模糊综合评价法的完整过程不再赘述。

1.1 6级隶属函数

隶属度rij可根据隶属函数的计算来确定。一般水质指标都是数值小者为优的成本型指标,即水质等级越高,其标准值越低。这种越小越优型指标采用“降半梯形”的函数表示,表达式如下:

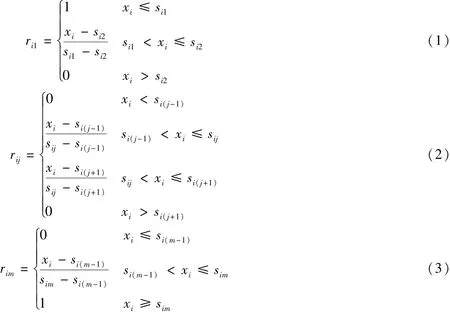
式中:xi——第i个评价因子质量浓度的实际监测值;Sij——第i个评价因子第j类水质的标准值。

对于DO这种数值大者为优的收益型指标,则采用“升半梯形”的函数表示,计算方法类似,由于篇幅有限,不再罗列其表达式。

在6级隶属函数的计算中,Sij不再代表各类水质的上下标准限值,而是上下限值的中间值。以CODMn为例,现行地表水水质标准Ⅰ至Ⅴ类分别为(0,2]、(2,4]、(4,6]、(6,10]、(10,15],若Sij取中间值,则可以得到Ⅰ类(0,1]、Ⅱ类(1,3]、Ⅲ类(3,5]、Ⅳ类(5,8]、Ⅴ类(8,12.5]、劣Ⅴ类(12.5,15]6个区间,相应地得到6个隶属函数与隶属度。

1.2 熵值赋权

传统的模糊综合评价法中,权重的确定一般采用评价因子贡献率的方法,即计算各评价指标质量浓度监测值相对于水质标准均值的超标比,再将归一化处理所获得的结果作为因子权重。这是一种主观赋权法,仅考虑单个因子的特征,而忽略了评价因子之间的联系;而且,评价对象数量众多时需重复计算每一对象每一评价指标的权重值,工作量较大。这是传统的模糊综合评价法的不足之处。

利用信息熵的概念确定权重,可有效克服传统赋权法的缺陷。信息熵表示系统的混乱程度,可以度量数据所提供的有效信息。水质由优变劣,实际上是水体中物质混乱程度增加的过程,即熵值增加的过程[16]。熵值赋权包括以下3个步骤[17]:

第1步:原始数据矩阵的标准化。假设有m个评价因子,n个评价对象,对原始数据进行标准化处理,得到矩阵

式中:rij——第i个评价因子在第j个评价对象上的标准值。

对数值大者为优的收益型指标而言,计算公式为

对数值小者为优的成本型指标而言,计算公式为

可得标准值rij∈[0,1]。

第2步:定义熵。数据标准化后,定义第i个评价因子的熵Hi,有

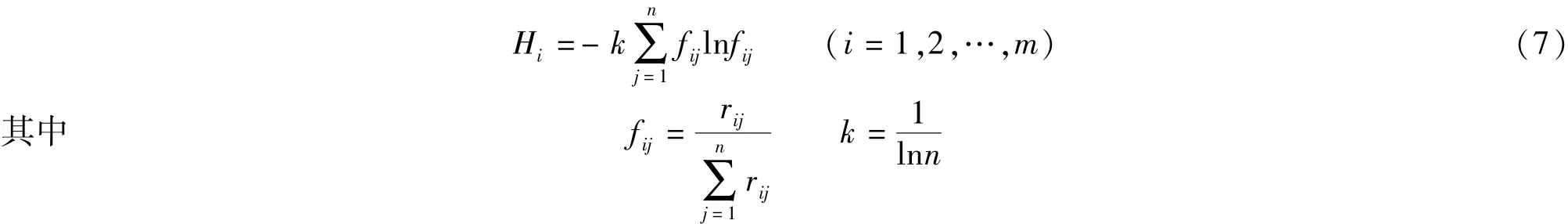
当fij=0时,令fijlnfij=0。

第3步:定义熵权。第2步完成后,可得到第i个指标的熵权值wi:

1.3 水质类别判定

传统的模糊综合评价法一般根据最大隶属度原则来判断水质类别,即,若模糊综合评价矩阵为B=(b1,b2,…,bn),bj=max(b1,b2,…,bn),待评价水体即为j类水质。由于考虑到最大隶属度原则会出现不适用性,改进的模糊综合评价法采用如下步骤来判定水质类别。

第1步:根据模糊综合评价矩阵,计算最大隶属度原则的有效度a[18]:

式中:n——模糊综合评价矩阵B中的元素个数;β——最大隶属度;γ——第2大隶属度。

计算有效度a,并得出如下结论[13]:当0.5≤a＜1时,最大隶属度原则比较有效;当0≤a＜0.5时,最大隶属度原则低效;当a=0时,最大隶属度原则完全失效。

第2步:对于有效度a大于0.5的监测断面,可采用最大隶属度原则评价水质类别;对于隶属度小于0.5的监测断面,采用置信度准则评价水质类别。

置信度准则[14]:设(C1,C2,…,Cn)是一个有序的水质评价集,λ为置信度,监测断面x属于Ci类水的隶属度为ux(Ci),记监测断面所属水质类别为Ck0,即有以下表达式:置信度准则是从“强”的角度考虑的,认为越“强”越好,而且“强”的类别应占的比例相当大。置信度λ一般取0.6与0.7之间,本文取0.68。

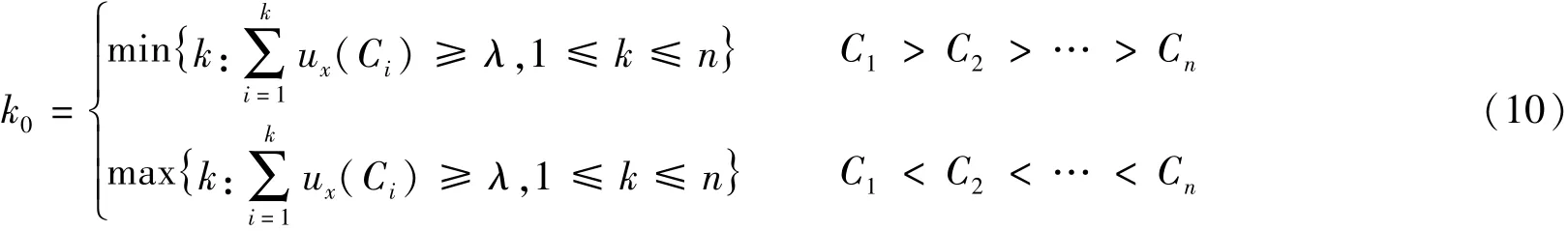
2 同里古镇水质评价

2.1 监测断面及数据来源

同里古镇设立了8个水质监测断面,分别为中元桥、吉利桥、蒋家桥、进口泵站、会川桥、饮马桥、东新桥和小东溪,具体位置分布见图1。其中“进口泵站”断面设立在引水泵站上游。“进口泵站”断面代表同里古镇外部水体;其余7个断面代表同里古镇内部水体。

研究所采用的监测数据为8个断面2012年3—8月的监测数据平均值。每个监测断面每月采样1次,采样时间均为每月下旬。

2.2 建立评价因子和评价集

在原始监测数据中,一共有20余项指标。同里古镇水质模糊综合评价模型中评价因子的选取主要根据以下2个原则:

a.排除某些不能直接利用国家地表水环境质量标准[19]来评判的监测指标,如硝态氮、透明度、浊度、电导率、叶绿素等。

b.排除某些监测值已经低于Ⅰ类水质标准的监测指标,如Hg、As、Cu、Zn等重金属指标。

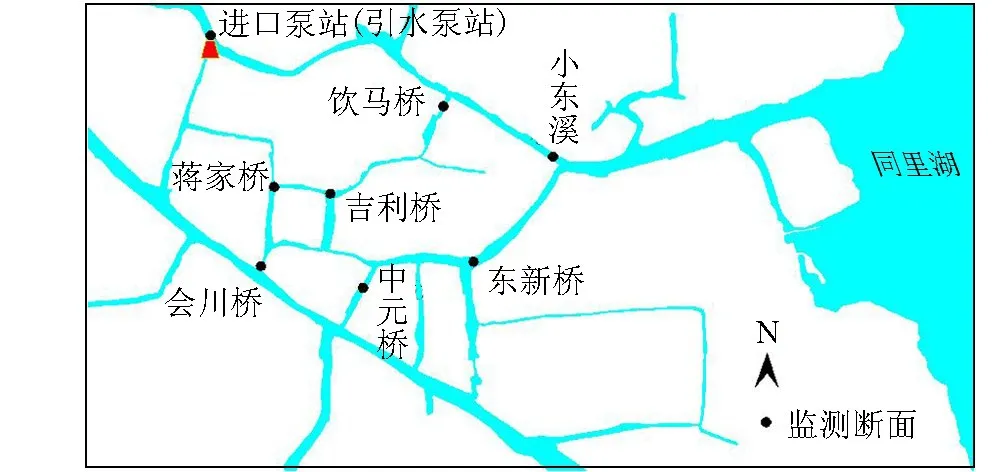
图1 同里古镇水质监测断面位置分布Fig.1 Locations of water quality monitoring sections in Tongli Town

最后筛选出DO、COD、CODMn、BOD5、TN、NH3-N、TP这7项常规指标作为同里古镇水质模糊综合评价模型的评价因子,组成评价因子集:

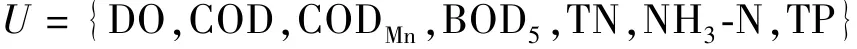
根据GB3838—2002《地表水环境质量标准》,地表水被分成了5类水质标准,故确定评价集为:V={Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ}。

上述7项评价因子在8个监测断面的监测值(3—8月的平均值)见表1。

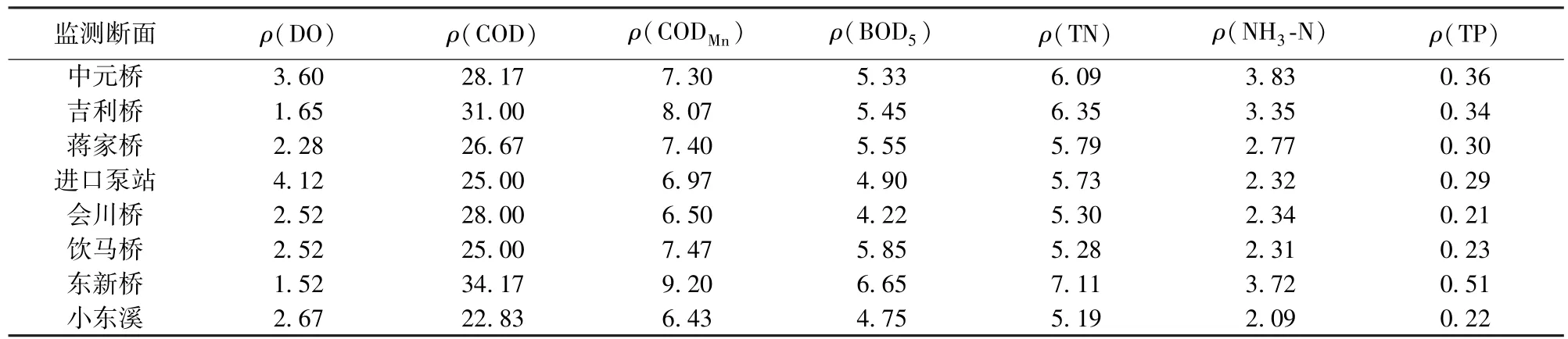
表1 7项评价因子在8个监测断面的监测值Table1 Values of seven indicators at eight monitoring sections mg/L

2.3 建立模糊关系矩阵

根据6级隶属函数的定义,计算每一个指标相对于Ⅰ～劣Ⅴ类水质的隶属度,可以得到8个断面水质的模糊关系矩阵。以中元桥断面为例,其隶属度矩阵为

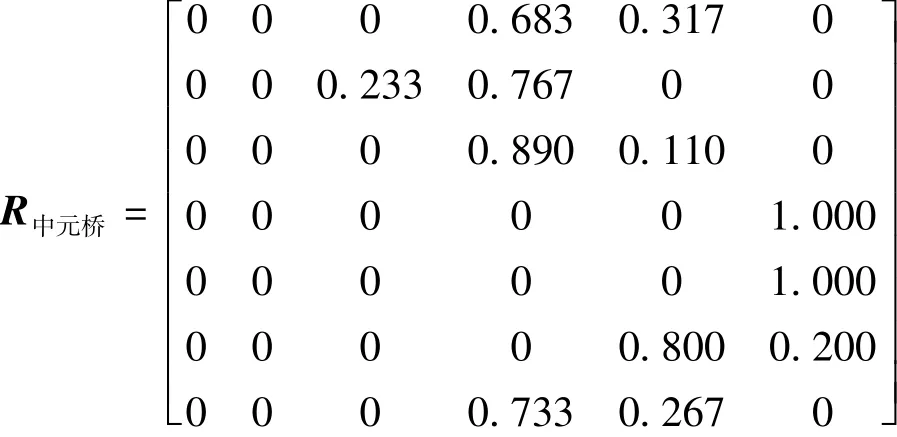
2.4 熵权的计算

根据式(4)～(8),计算各因子的熵以及熵权,结果见表2。评价因子信息熵的大小与该项评价因子在各个监测断面上监测值的差异程度成反比。如因子TP,8个监测断面的监测值相差较小,熵值就较大,说明因子TP提供的有效信息量较小,该指标的权重就相应较小。如果某项指标在各被监测断面上的值完全相同,那么可以认为熵值达到最大,就意味着该指标未向决策提供任何有用的信息,可以考虑从评价指标体系中去除[20]。

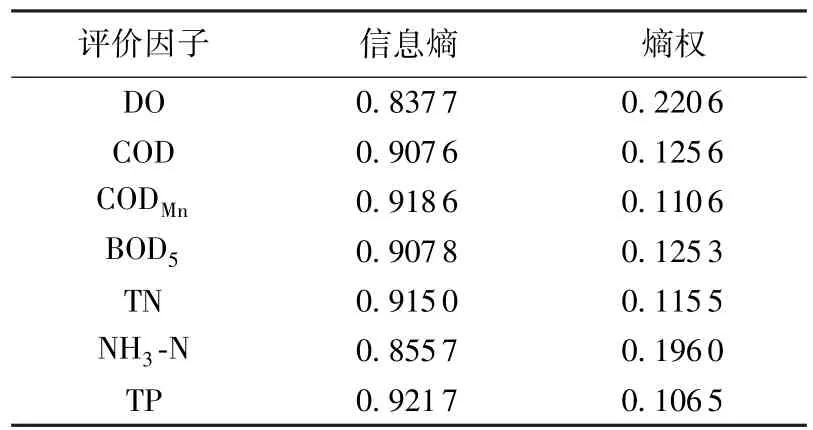
表2 各因子熵及熵权Table2 Entropies and weights of indicators

2.5 判定水质类别

利用各监测断面水质的模糊关系矩阵与各评价因子的权重集的乘积,可得出水质模糊综合评价矩阵,根据各水质类别综合隶属度,可计算最大隶属度原则的有效度a,计算结果见表3。

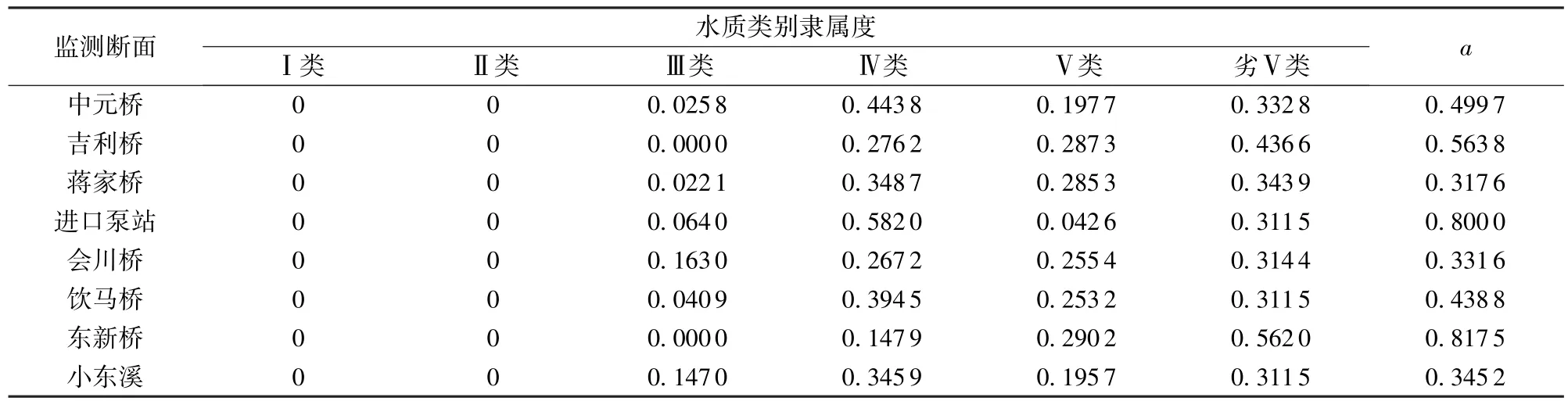
表3 最大隶属度原则的有效度计算结果Table3 Effective degree of maximum membership degree principle

从表3可以看出,适合用最大隶属度原则来判定水质的只有吉利桥、进口泵站和东新桥断面,其水质类别分别为劣Ⅴ类、Ⅳ类、劣Ⅴ类。其余断面a值均低于0.5,最大隶属度原则低效,需采用置信度准则(λ= 0.68)来判断水质类别。对于水质评价,可认为水质类别越低置信度越“强”,如会川桥断面,(0+0+0.1630+0.2672+0.2554)=0.6857＞0.68,其水质为Ⅴ类。

2.6 评价结果与讨论

利用改进的模糊综合评价模型,对同里古镇8个断面的水质进行评价,评价结果见表4。同时利用传统模糊综合评价模型进行同里古镇水质评价,得出评价结果见表5。将这两种评价结果进行对比讨论。

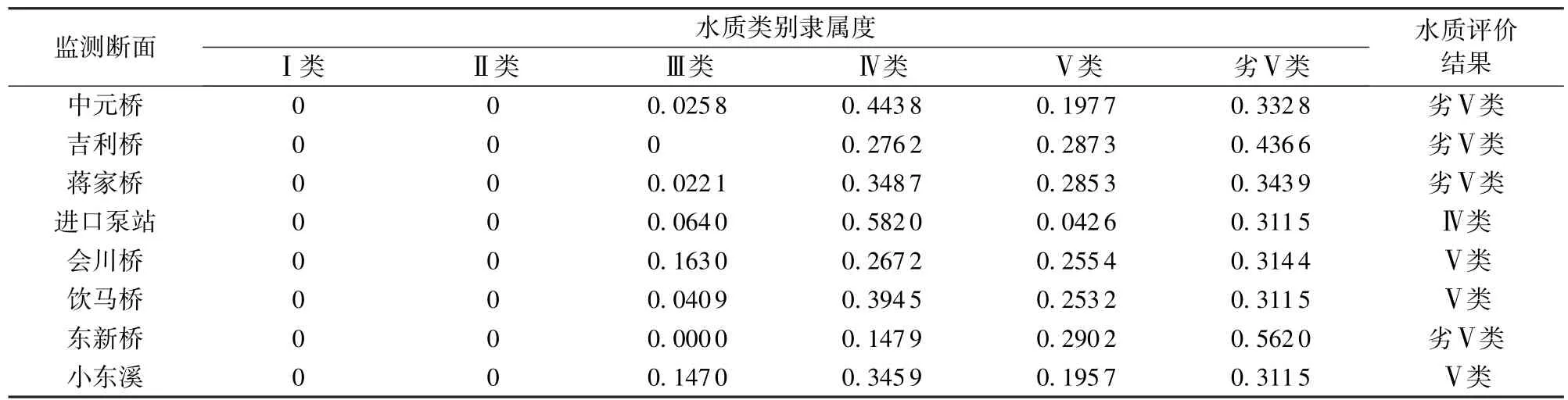
表4 改进的模糊综合评价法水质评价结果Table4 Evaluation results of improved fuzzy comprehensive evaluation method

a.利用传统的模糊综合评价法,同里古镇的水质类别全部属于Ⅴ类。但根据监测断面的设置情况以及监测数据,进口泵站断面属于古镇外部水系,各水质因子明显优于其他断面,表明传统的模糊综合评价法得出水质评价结果明显与事实不符。而采用改进的模糊综合评价模型进行水质评价,结果表明,进口泵站断面水质为Ⅳ类,优于其余古镇内部监测断面的水质,说明利用改进的模糊综合评价模型进行水质评价更加具备区分度,评价结果符合实际情况。

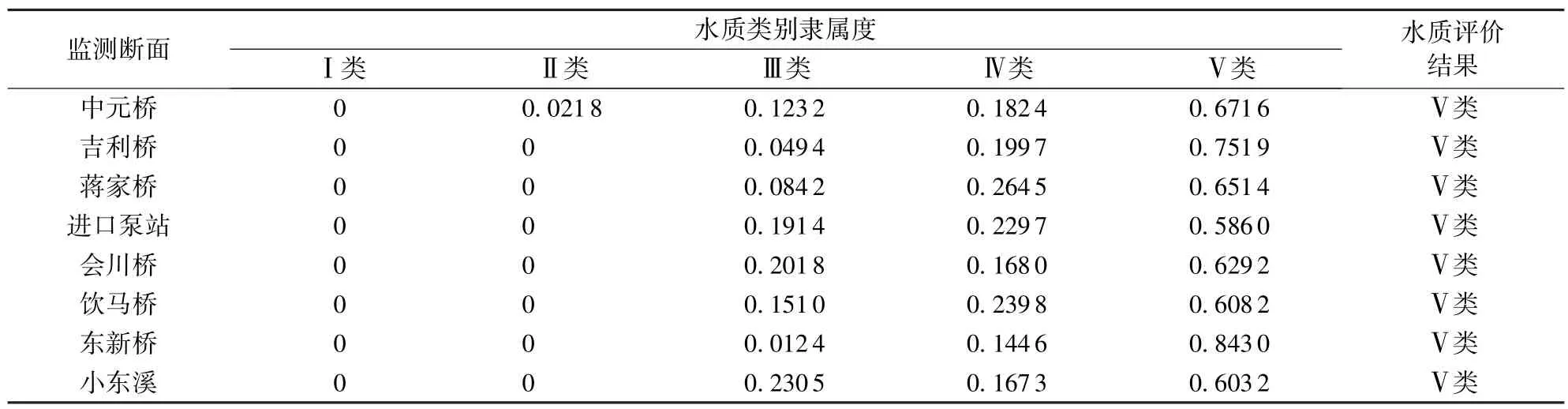
表5 传统的模糊综合评价法水质评价结果Table5 Evaluation results of traditional fuzzy comprehensive evaluation method

b.改进的模糊综合评价法对劣Ⅴ类水质的判断弥补了传统模糊综合评价法的不足,扩大了评价范围。对水质超出Ⅴ类的水体,改进的模糊综合评价法是一种比较适用的水质评价方法。

c.传统的模糊综合评价法通过超标比来确定权重,需进行8次权重设计,而改进的模糊综合评价法采用熵权来确定权重,一次可确定7个水质评价因子的权重,减少了计算量,而且通过分析熵值,可确定影响同里古镇水质最严重的因子是DO和NH3-N,表明古镇水体受耗氧有机物污染严重,污染主要源自生活污水,这是传统赋权法无法做到的。

d.若利用最大隶属度原则对水质类别进行判断,得出评价结果均要比表4中结果低1～2个类别,如中元桥断面将被判为Ⅳ类,小东溪断面也将被判为Ⅳ类。这说明利用改进的模糊综合评价法的水质判定原则,不会低估水体的受污染程度。对于综合隶属度相差不大、水质类别不清的断面,利用最大隶属度原则可能存在问题,如蒋家桥断面的Ⅳ类水质的隶属度为0.3487,Ⅴ类水质的隶属度为0.2853,劣Ⅴ类水质的隶属度为0.3439,利用最大隶属度原则将蒋家桥断面的水质评价为Ⅳ类,显然是有问题的,因为该断面水质的Ⅴ类和劣Ⅴ类隶属度之和已经大于0.3487,而改进的模糊综合评价法则可对此给出很明确的解释和判断。

e.有效度指标a不仅可以判断最大隶属度原则是否有效,还可以解释用最大隶属度原则确定某水质类别的相对置信度,如对于蒋家桥断面,采用最大隶属度原则进行水质评价,只有31.76%的把握认定其水质属于Ⅳ类。若将置信度概念与置信度准则中λ相统一,取a=λ=0.68,最终评价结果与表4一致。但这并不说明最大隶属度原则的有效度a与置信度准则的置信度λ是同一概念,两者是否有直接联系,需要进一步研究和讨论。

3 结 论

a.将6级隶属函数、熵权、最大隶属度原则有效度和置信度准则有机结合的改进的模糊综合评价法应用于同里古镇水质评价,结果表明这是一种合理、可靠且更全面的水质评价方法,值得在类似同里古镇这种产业密集型镇域的水系水质评价中推广。

b.作为国家5A级风景区和江南著名水乡古镇,同里古镇目前的水质状况不容乐观,所有监测断面的水质均为Ⅴ类和劣Ⅴ类,水系内部断面已无法满足水域功能区划的要求。

c.建议今后在同里水系采用更加直观且包含信息更加全面的水质评价方法,如进行全时段的水质变化综合评价,增加浮游植物或动物等生态指标,完善评价指标体系,建立突破现行地表水分类标准限制的评价体系等。

[1]吴运敏,陈求稳,李静,等.模糊综合评价在小流域河道水质时空变化研究中的应用[J].环境科学学报,2011,31(6): 1198-1205.(WU Yunmin,CHEN Qiuwen,LI Jing,et al.Fuzzy comprehensive assessment on spatio-temporal variations of water quality of a small catchment[J].Acta Scientiae Circumstantiae,2011,31(6):1198-1205.(in Chinese))

[2]王新智,张虎子,贾振,等.基于单项指数法和模糊综合评价法对松花江吉林市段水质的评价[J].环境科学与管理, 2012,37(9):184-187.(WANG Xinzhi,ZHANG Huzi,JIA Zhen,et al.Application of single index method and fuzzy comprehensive method in water quality evaluation of Jilin City Section of Songhua River[J].Environmental Science and Management,2012,37(9):184-187.(in Chinese))

[3]潘怡,仵彦卿,叶属峰,等.上海海域水质模糊综合评价[J].海洋环境科学,2009,28(3):283-287.(PAN Yi,WU Yanqing,YE Shufeng,et al.Comprehensive assessment of seawater quality by fuzzy mathematical model around Shanghai sea [J].Marine Environmental Science,2009,28(3):283-287.(in Chinese))

[4]孙靖南,邹志红,任广平,等.模糊综合评价在天然水体水质评价中的应用研究[J].环境污染治理技术与设备,2005, 6(2):45-48.(SUN Jingnan,ZOU Zhihong,REN Guangping,et al.Study on the fuzzy synthetic evaluation for natural water quality[J].Techniques and Equipment for Environmental Pollution Control,2005,6(2):45-48.(in Chinese))

[5]徐兵兵,张妙仙,王肖肖,等.改进的模糊层次分析法在南苕溪临安段水质评价中的应用[J].环境科学学报,2011,31 (9):2066-2072.(XU Bingbing,ZHANG Miaoxian,WANG Xiaoxiao,et al.Application of an improved fuzzy analytic hierarchy process in water quality evaluation of the South Tiaoxi River,Lin'an Section[J].Acta Scientiae Circumstantiae, 2011,31(9):2066-2072.(in Chinese))

[6]王涛,魏亚妮,钱会,等.权重对水质模糊综合评价的影响[J].南水北调与水利科技,2010,8(2):87-90.(WANG Tao,WEI Yani,QIAN Hui,et al.Influence of different weights on fuzzy comprehensive evaluation method for water quality[J].South-to-North Water Transfers and Water Science&Technology,2010,8(2):87-90.(in Chinese))

[7]吴明发,欧名豪,朱咏佳,等.基于信息熵的鹤山市土地利用结构时空变化研究[J].国土与自然资源研究,2012(4): 25-27.(WU Mingfa,OU Minghao,ZHU Yongjia,et al.Temporal-spatial changes in land use structure based on information entropy in Heshan City[J].Territory&Natural Resources Study,2012(4):25-27.(in Chinese))

[8]朱吉祥,张礼中,周小元,等.基于信息熵的灰色模型在地质灾害评价中的应用:以四川青川县为例[J].灾害学, 2012,27(1):78-82,97.(ZHU Jixiang,ZHANG Lizhong,ZHOU Xiaoyuan,et al.Application of entropy-based grey model in geological hazard assessment:a case study of Qingchuan County,Sichuan Province[J].Journal of Catastrophology,2012,27 (1):78-82,97.(in Chinese))

[9]孔雪松.基于信息熵的区域环境安全评价:以武汉市为例[J].资源开发与市场,2007,23(1):18-20.(KONG Xuesong.Assessment of region environment security based on Shannon Entropy:a case study of Wuhan[J].Resource Development& Market,2007,23(1):18-20.(in Chinese))

[10]MOGHEIR Y,LIMA J L,de LIMA M P,SINGH V P,et al.Entropy and multi-objective based approach for groundwater quality monitoring network assessment and redesign[J].Water Resources Management,2009,23(8):1603-1620.

[11]孟宪萌,胡和平.基于熵权的集对分析模型在水质综合评价中的应用[J].水利学报,2009,40(3):257-262.(MENG Xianmeng,HU Heping.Application of set pair analysis model based on entropy weight to comprehensive evaluation of water quality[J].Journal of Hydraulic Engineering,2009,40(3):257-262.(in Chinese))

[12]方正,孙迎霞,程晓如,等.多级模糊模式识别方法用于湖泊水质评价[J].三峡环境与生态,2003,25(10):39-41, 45.(FANG Zheng,SUN Yingxia,CHENG Xiaoru,et al.Using mulitilevel fuzzy identification way to evaluate lake water quality [J].Environment and Ecology in the Three Gorges,2003,25(10):39-41,45.(in Chinese))

[13]郭东星,何大卫.最大隶属原则的有效度在模糊综合评价中的作用[J].山西医科大学学报,1998,29(2):128-130.(GUO Dongxing,HE Dawei.The function of the effective degree of maximum membership degree principle in fuzzy comprehensive evaluation[J].Journal of Shanxi Medical University,1998,29(2):128-130.(in Chinese))

[14]程乾生.属性识别理论模型及其应用[J].北京大学学报:自然科学版,1997,33(1):12-20.(CHENG Qiansheng.Attribute recognition theoretical model with application[J].Acta Scientiarum Naturalium Universitatis Pekinensis,1997,33(1): 12-20.(in Chinese))

[15]贺玉龙,戴本林,陶雪峰,等.基于置信度准则的地表水水质模糊综合评价[J].中国给水排水,2011,27(23):52-55.(HE Yulong,DAI Benlin,TAO Xuefeng,et al.Fuzzy comprehensive evaluation of surface water quality based on confidence criteria[J].China Water&Wastewater,2011,27(23):52-55.(in Chinese))

[16]王玉萍,何玛峰.水质状况的熵值评价法[J].河北水利水电技术,2001(1):36-38.(WANG Yuping,HE Mafeng.Evaluation method of entropy value of water quality condition[J].Hebei Water Resources and Hydropower Technology,2001 (1):36-38.(in Chinese))

[17]ZOU Zhihong,YUN Yi,SUN Jingnan.Entropy method for determination of weight of evaluating indicators in fuzzy synthetic evaluation for water quality assessment[J].Journal of Environmental Sciences,2006(5):1020-1023.

[18]王静,董肖丽.模糊评价中最大隶属度原则的改进[J].河北水利,2011(2):27-28.(WANG Jing,DONG Xiaoli.Improvement of the principle of maximum membership degree in fuzzy comprehensive evaluation[J].Hebei Water Resources, 2011(2):27-28.(in Chinese))

[19]GB 3838—2002 地表水环境质量标准[S]

[20]邱宛华.管理决策与应用熵学[M].北京:机械工业出版社,2002.

Application of improved fuzzy comprehensive evaluation to water quality evaluation in Tongli Town

XU Jian1,WU Wei1,HUANG Tianyin1,JIA Haifeng2
(1.School of Environmental Science and Engineering,Suzhou University of Science and Technology, Suzhou 215009,China; 2.Department of Environmental Science and Engineering,Tsinghua University,Beijing 100084,China)

Based on monitoring results from eight monitoring sections in Tongli Town from March to August in 2012,an improved fuzzy comprehensive evaluation method was used to evaluate the water quality in this town.Six membership functions and entropy weight were used in this method,and ultimate water quality classification was judged by the effective degree of the maximum membership degree principle and the confidence criteria.The improved fuzzy comprehensive evaluation method was compared with the traditional fuzzy comprehensive evaluation method.The results show that the internal water quality of the town reached gradeⅤor a point inferior to gradeⅤ,and the external water quality was better than the internal one.Compared with the traditional method,the improved method shows better performance in distinguishing different grades of water quality and can be used to evaluate water quality inferior to grade V,it has a simple weight calculation and can determine the main pollution factors,and the evaluation results are more reasonable and reliable.

water quality evaluation;improved fuzzy comprehensive evaluation;six membership function;entropy weight;confidence criteria;Tongli Town

X824

:A

:1000-1980(2014)02-0143-07

10.3876/j.issn.1000-1980.2014.02.009

2013-01 29

水体污染控制与治理科技重大专项(2011ZX07301-003);苏州市科技支撑计划(ss201107)

徐健(1988—),男,江苏常州人,硕士研究生,主要从事排水工程理论与基础研究。E-mail:358442086@qq.com

吴玮,副教授。E-mail:222601107@qq.com