一种非最小相位系统的非线性控制器设计方法

金晓孝，王万成

(河海大学能源与电气学院，江苏南京 210098)

近30年来，微分几何方法在非线性控制系统中得到了广泛的应用，形成了较完善的理论体系［1］。通过非线性坐标变换和相应的状态反馈将一个非线性系统进行输入输出线性化，再对线性子系统设计控制器是一种有效的非线性系统控制方法，但是运用此方法的前提是要求非线性系统必须是最小相位的［2］。然而，具有非最小相位特性的非线性系统在实际工程中却广泛存在，例如化工系统［3-4］、鱼雷定深系统［5］、飞行器俯仰控制系统［2］、水轮机调节系统［6］等，因此系统的非最小相位特性使得微分几何反馈线性化方法在实际工程应用中遇到了极大挑战。为此，Kravaris等［7-8］通过输出重定义的方法解决了在输入输出线性化过程中不能保证其内部状态稳定的问题，程代展等［9］利用中心流形定理对具有非最小相位特性的非线性系统设计了控制器，袁德成等［10］提出了非线性辅助控制系统以解决对非线性非最小相位系统的控制器设计问题，Okou等［11］基于李雅普诺夫稳定理论对零动态不稳定的系统给出了控制器的设计方法。

本文在文献［11］控制器设计方法的基础上，给出了一种改进的非最小相位系统的非线性控制器设计方法，该方法消除了原方法中可能因扰动等因素使分母暂时为零而导致控制器失效的情况，同时该控制器在确保外部系统满足性能要求的同时也能保证零动态的稳定，数值算例仿真结果验证了该方法的有效性。

1 非线性系统的精确反馈线性化

以下对基于微分几何的精确反馈线性化理论作一简要介绍［1，12］。给定如下的单输入单输出非线性控制系统:

式中:x——n维状态列向量;f(x)、g(x)——状态空间中的n维光滑向量场;u——控制输入;y——被控输出;h(x)——输出函数。

如果非线性系统(1)的相对阶为r［1］，则可以选择微分同胚映射:

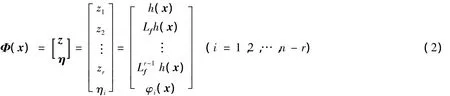
式中φi(x)满足关系Lgφi(x)=0，同时要求Φ(x)在x=x0点处的Jacobian矩阵非奇异，可将非线性系统(1)转换为下列线性化标准型:

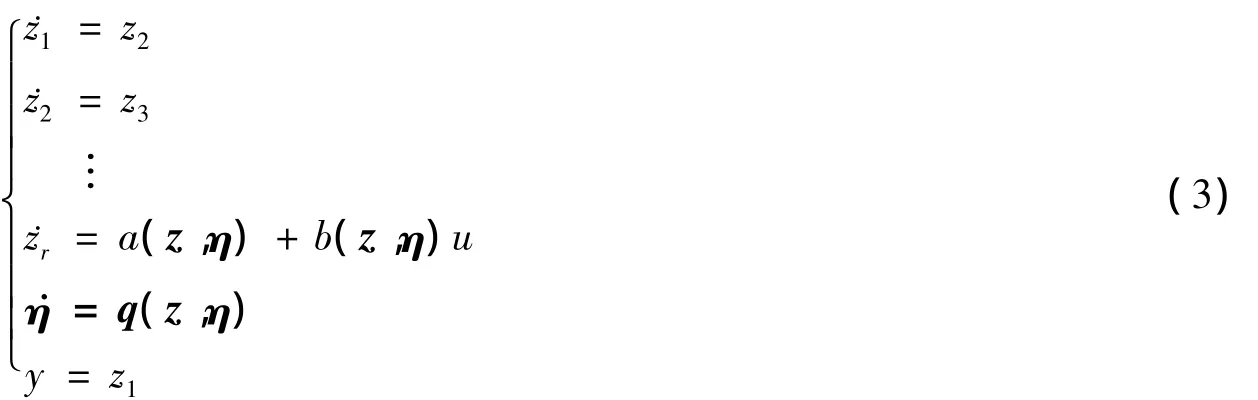
其中

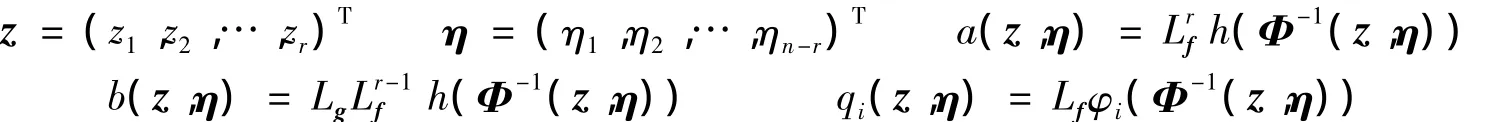
线性化标准型(3)把系统分解为外部动态z和内部动态η两部分。定义˙η=q(0，η)为非线性系统的零动态方程，如果零动态不稳定则称系统是非最小相位的。令a(z，η)+b(z，η)u=v，可见状态反馈控制u=(v-a(z，η))/b(z，η)可使外部动态z线性化，但该控制使得内部状态η变为不可观测的状态。

传统的控制方法是对线性化后的线性子系统按照线性系统理论来设计控制器，这样设计的控制器对于线性部分的控制是有效的，但它并不能保证零动态η稳定，甚至是发散的。这将给系统安全运行带来严重影响，而且由于控制能量的限制使得设计的控制器在物理上难以实现，所以必须采用一定的控制方法来克服系统的非最小相位特性。

2 系统控制器设计方法

考虑非线性系统(1)，首先按微分几何方法将其化为线性化标准型(3)，然后将其中的非线性子系统部分做下述处理:

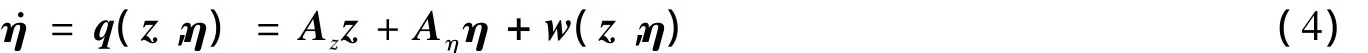
其中

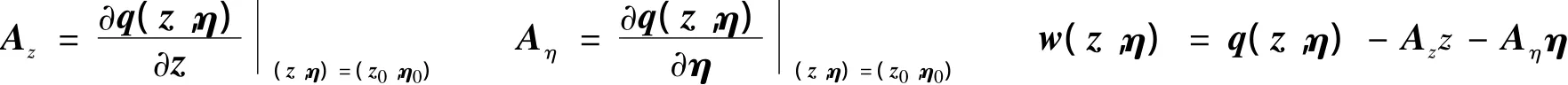
式中z0、η0是线性化标准型的平衡点。

结合式(4)，可将式(3)写成下列等价形式:

其中

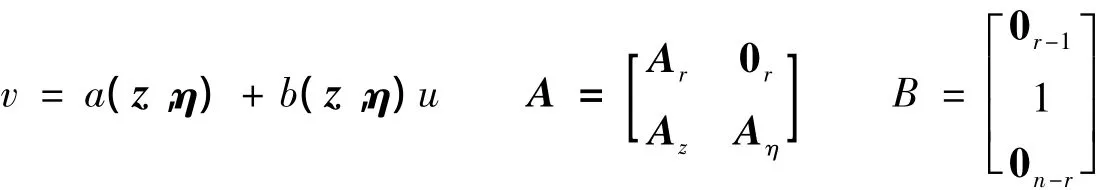
假定系统(5)的控制器为

其中

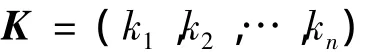
式中:K——行增益向量;vNL——为了使非线性子系统稳定而引入的补偿项。将式(6)所述的控制器代入被控系统(5)可得如下闭环系统:

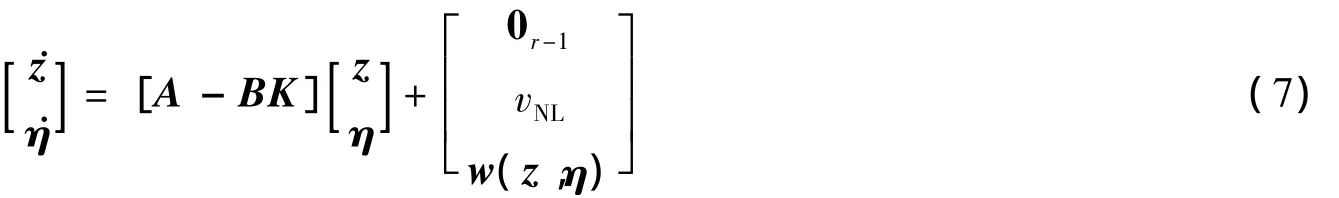
选择K使得As=［A-BK］为Hurwitz矩阵，同时构造以下李雅普诺夫函数:

其中P是满足如下李雅普诺夫方程的正定矩阵(一般可选Q为单位矩阵I):

根据李雅普诺夫稳定性定理［13］，要使控制作用下的闭环系统(7)稳定，只要L˙(z，η)＜0即可。由于Q是正定的，只需

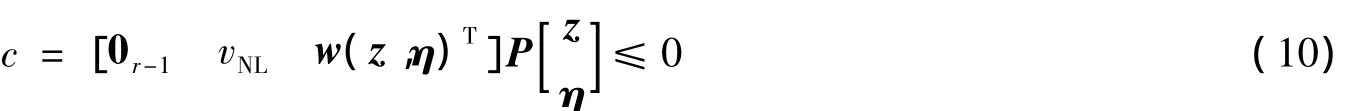
令c=0，从式(10)可解出vNL，即有

式中 Pi是矩阵 P 中各行向量，wi(z，η)由 w(z，η)=(wr+1(z，η)，…，wn(z，η))T确定。

根据上述过程可以得到式(6)所述非最小相位系统的非线性控制器，最后利用v=a(z，η)+b(z，η)u反解出

式(12)就是原非最小相位系统(1)的最终控制器。该控制器设计方法主要做了以下几点改进:

a.该方法适用的充分必要条件是式(5)中的矩阵对(A，B)是完全能控的，即能控性矩阵 Qc=[B AB…An-1]满足 rank(Qc)=n。

b.显然，式(4)的分解是该控制器设计方法的关键。对于式(4)的分解作以下改进:(a)如果非线性函数q(z，η)不满足式(4)所给定的形式，就要将其化为式(4)的形式，式中的w(z，η)可由下式确定:

在复杂的实际工程应用时按此方法分解所设计的控制器将十分复杂，尤其是在实际工程应用时，由于被控系统具有复杂非线性特征，这样非线性函数q(z，η)中通常会含有分母项，按此方法分解可能会出现分母暂时为零的情况而导致控制器失效。(b)针对上面这种情况，可作如下改进:在式(4)的基础上，进一步将非线性函数w(z，η)进行泰勒展开，只保留至二阶或三阶项(甚至可以保留至更高阶项，这可根据工程实际来确定)。由于舍去的高阶小项所引起的误差与建模或外界不确定因素所引入的误差相比是非常微小的，所以这种改进是合理的，而且更适合工程应用，拓展了该方法的适用范围。

c.式(10)中，常数c理论上尽管可以选为小于零的负数来求解vNL，但仿真实验表明这样做对控制性能影响不是很大，因此一般选择c=0即可。

上述控制器设计方法是在微分几何精确反馈线性化方法基础上给出的，与一阶近似线性化方法相比，其系统信息丢失也较少，这主要体现在两个方面:首先，该方法是在对原系统进行精确反馈线性化后，只对系统的一部分状态方程˙η=q(z，η)进行泰勒展开，而非对整个非线性系统进行展开;其次，对非线性函数w(z，η)的泰勒展开，可以进一步通过提高其展开的阶次(比如可保留至三阶或四阶)来尽可能地减少系统信息的丢失。

3 数值算例

下面以两个数值算例来说明上面给出的控制器设计方法(以下简称本文方法)及其仿真效果，其中例1主要是说明控制器的设计步骤以及与传统非线性控制器的控制效果进行对比，例2主要是说明本文方法的改进之处。

例1 考虑下列非线性非最小相位系统:

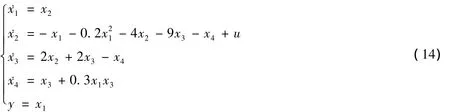
该系统具有式(3)所述的线性化标准型形式，显然是非最小相位系统。控制目标:设计控制器使输出y=x1能够稳定在设定点0上，且在该控制器作用下系统的零动态能够稳定。

a.按照传统的控制器设计方法设计控制器。为叙述方便，线性子系统单独列出如下:

其中

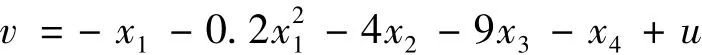
将上述线性子系统的极点配置到-3±i，可以得到状态反馈控制律v=-10x1-6x2，再结合-4x2-9x3-x4+u=v可以得到控制器u，在此控制器下仿真效果如图1和图2所示。从图1和图2中可以看出，尽管传统控制器设计方法可以很好地使输出y=x1满足设计的要求，但却不能保证零动态x3和x4稳定。

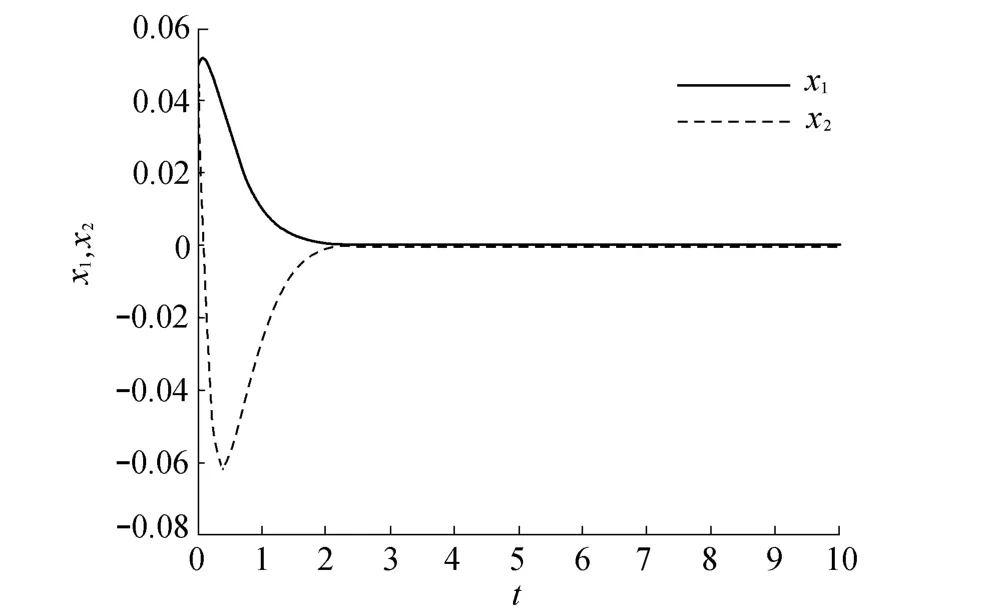
图1 状态x1和x2(传统方法)Fig.1 State of x1 and x2(traditional method)

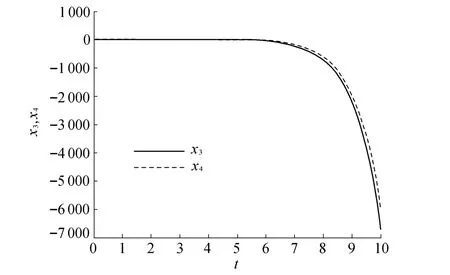
图2 状态x3和x4(传统方法)Fig.2 State of x3 and x4(traditional method)

b.按本文方法设计控制器。首先将原非线性系统改写为式(5)的形式，设控制器为v=-Kx+vNL，将As=［A-BK］的4个极点配置到 -1±i、-3、-5上，则满足条件的 K为 K=(30，12，13，47)。取 Q=I，由可以计算出正定矩阵P，再由(0，v，

NL0，0.3x1x3)Px=0可以解得vNL，从而得到v=-K，再从中反解出u，这样便得到了非线性非最小相位系统(14)的控制器。在该控制器的控制作用下，系统的4个状态变量的控制效果如图3所示。

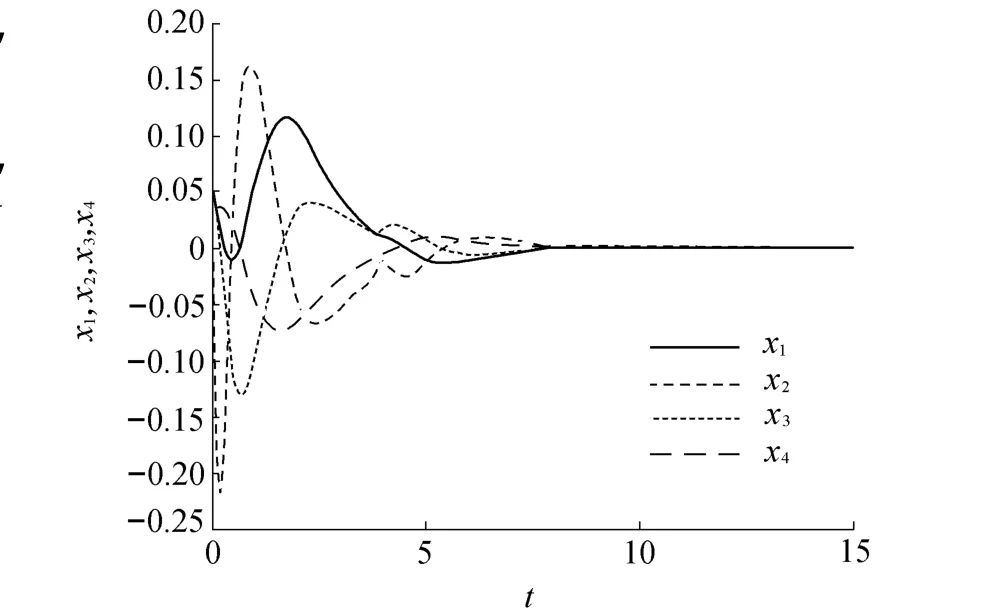
图3 状态x的控制效果Fig.3 Control effect of state x

从图3可以看出，本文方法不仅保证了外部动态y=x1的性能要求，还保证了零动态x3和x4的稳定。

例2 给定非线性非最小相位系统如下:

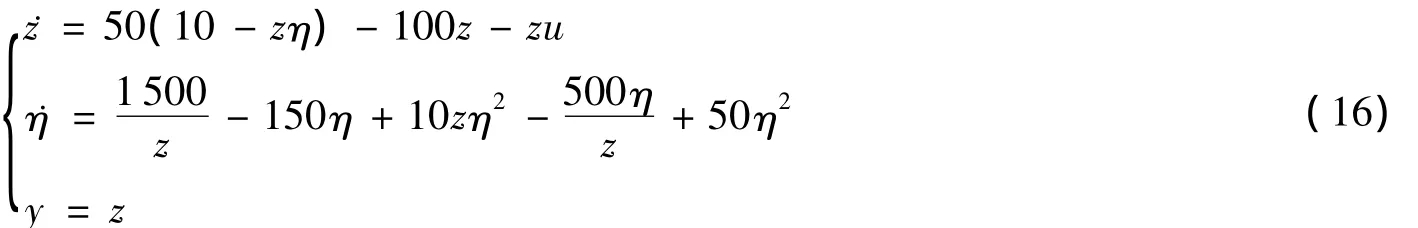
控制目标是将y=z调节到给定点1.05上。类似于例1，容易验证:传统的非线性控制器设计方法尽管可以保证y=z满足性能要求却并不能保证零动态η稳定。

根据本文方法，将式(16)中的第2个状态方程记为

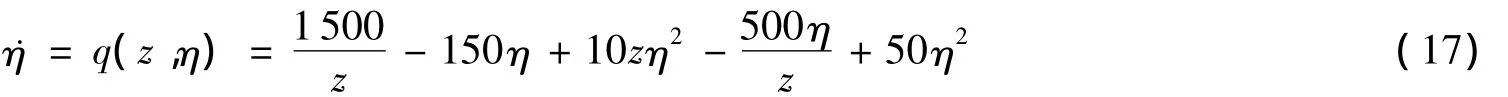
如果按照文献［11］中的分解方法，将式(17)按照式(13)来进行分解，尽管经过数学推导也可以得到控制器，但得到的控制器在形式上非常复杂，而且该控制器会出现分母为零的情况，导致仿真难以进行而使得控制器失效。为此，依据本文方法来对式(17)进行分解。

在状态(z，η)=(1.05，6.9552)处，通过二阶泰勒展开，式(17)可分解为

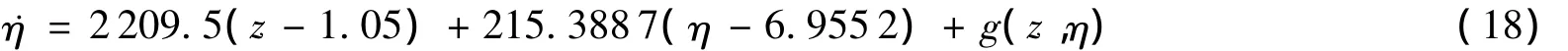
其中g(z，η)=-1708.3(z-1.05)2+60.5(η-6.9552)2+296.3093(z-1.05)(η-6.9552)

令50(10-zη)-100z-zu=v，根据式(6)，系统的控制器可设为v=-k1(z-1.05)-k2(η-6.9552)+vNL。根据前面的设计步骤，将系统的极点配置到-15±9i，可以得到k1=245.388 7，k2=24.059 7，再利用式(9)及式(10)便可确定最终的控制器。在此控制器的作用下，控制效果如图4和图5所示，可见此控制器既可以保证y=z满足性能要求同时也能保证零动态η稳定。

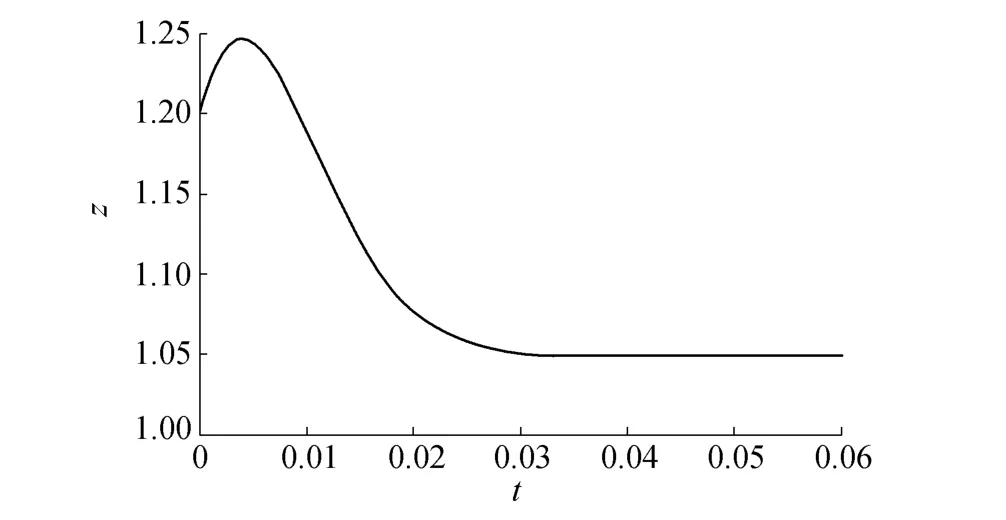
图4 状态z的控制效果Fig.4 Control effect of state z

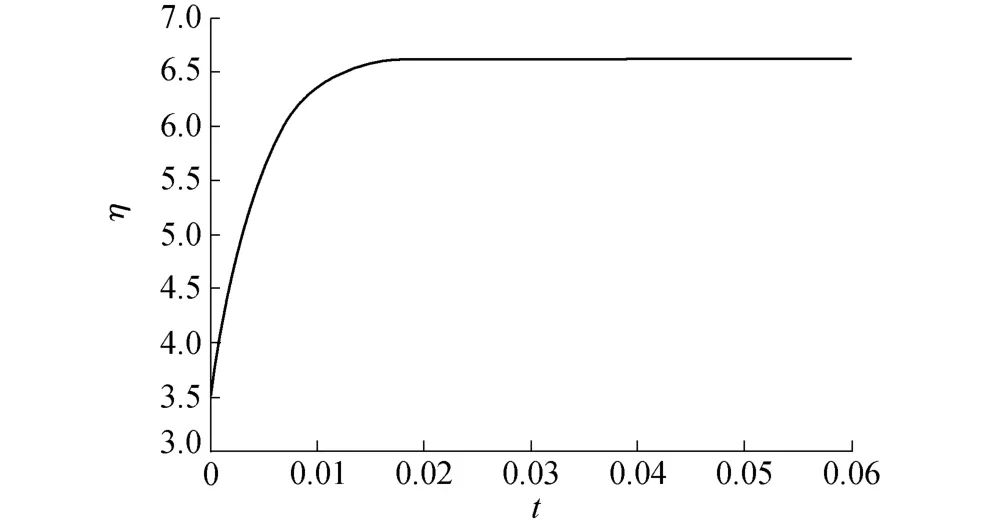
图5 零动态η的控制效果Fig.5 Control effect of zero dynamicη

由例2可以看出:(a)与文献［11］中的方法相比，本文方法适用范围更广、更加实用;(b)由式(18)可以看出，与传统的一阶近似线性化方法相比，本例只对零动态部分进行了泰勒展开，而且泰勒展开过程中保留了二阶项，这样便保留了非线性系统的更多信息，从而使得控制器保持了良好的控制性能。

4 结 语

本文借鉴文献［11］的控制器设计思想，在微分几何精确反馈线性化理论的基础上，基于极点配置和李雅普诺夫稳定理论，以单输入单输出非线性系统为被控对象，给出了一种改进的非最小相位系统的非线性控制器设计方法。该方法在确保系统外部动态满足性能要求的同时也能保证零动态的稳定。本文所给出的控制器设计方法是建立在微分几何精确反馈线性化基础上的，与近似线性化方法相比，能够保留更多的非线性系统信息，从而使得所设计的控制器具有较好的控制性能。该方法易于实现，便于工程应用。将该方法进一步推广到多输入多输出非线性系统，是我们后续的研究工作之一。

［1］卢强.电力系统非线性控制［M］.2版.北京:清华大学出版社，2008.

［2］BENVENUTI L，BENEDETTOM D D.Approximate output tracking for nonlinear non-minimum phase systems with an application to flight control［J］.International Journal of Robust and Nonlinear Control，1994，4:397-414.

［3］NIEMIEC M，KRAVARISC.Controller synthesis for multivariable nonlinear non-minimum phase processes［J］.Proceedings of American Control Conference，1998，4:2076-2080.

［4］NIEMIEC M，KRAVARISC.Nonlinear model-state feedbacKcontrol for non-minimum phase processes［J］.Automatic，2003，39:1295-1302.

［5］刘翔，李东海，姜学智，等.不稳定对象及非最小相位的自抗扰控制仿真研究［J］.控制与决策，2001，16(4):420-424.(LIU Xiang，LI Donghai，JIANG Xuezhi，et al.Simulation study on auto-disturbance-rejection control unstable systems and nonminimum phase systems［J］.Control and Decision，2001，16(4):420-424.(in Chinese))

［6］方红庆，沈祖饴，吴恺.水轮机调节系统非线性解耦控制［J］.中国电机工程学报，2004，24(3):151-155.(FANGHongqing，SHEN Zuyi，WU Kai.Nonlinear disturbance decoupling control for hydraulic turbogenerators regulation system［J］.Proceedings of the CSEE，2004，24(3):151-155.(in Chinese))

［7］KRAVARIS C，NIEMIEC M，KAZANTZIS N.Singular PDEs and the assignment of zero dynamics in nonlinear system［J］.Systems ＆ Control Letters，2004，51:67-77.

［8］HU Aiping，SADEGH N.Nonlinear non-minimum phase output tracking via output redefintion and learning control［J］.Proceedings of the American Control Conference，2001，6:4264-4269.

［9］CHEN Daizhan，MARTIN C.Stabilization of nonlinear systems via designed center manifold［J］.IEEE Transactions on Automatic Control，2001，46(9):1372-1383.

［10］袁德成，韩阳，王贵成，等.非线性辅助内模控制的研究［J］.信息与控制，1995，24(4):231-236.(YUAN Decheng，HAN Yang，WANG Guicheng，et al.Auxiliary internal model control strategy for nonlinear systems［J］.Information and Control，1995，24(4):231-236.(in Chinese))

［11］OKOU A F，AKHRIF O，DESSAINT L A.Nonlinear control of non-minimum phase systems:application to the voltage and speed regulation of power systems［J］.Proceedings of IEEE，International Conference on Control Application，1999(1):609-615.

［12］ISIDORI A.Nonlinear Control Systems［M］.3rd ed.Berlin:Springer-Verlag，1994.

［13］KHALIL H K.Nonlinear Systems［M］.New Jersey:Pearson Education，2002.