含电动汽车的微网系统多目标经济调度

庄怀东 吴红斌 刘海涛 季 宇

（1.合肥工业大学电气与自动化工程学院 合肥 230009 2.中国电力科学研究院 北京市 100192）

1 引言

电动汽车（Electric Vehicle，EV）的大规模接入势必会给电网带来诸多影响[1]，大量电动汽车的无序充电不仅会加重电网负荷高峰时的负担，还会影响系统电压和频率。随着电动汽车入网（Vehicle to Grid，V2G）概念[2]的提出，这些问题可能会得到缓解。V2G，即电动汽车作为储能单元，在停驶时可以通过一定的连接装置向电网回送功率，在车网之间实现电能双向传输。因此，将可入网电动汽车引入微网系统，考虑电动汽车有序充放电控制，结合分布式电源的应用[3]，可达到削峰填谷的作用，同时增加系统的经济性。

微网系统的经济调度，是在计及安全约束的前提下，采用不同目标函数，通过合理分配各分布式电源出力以解决负荷需求的基本问题。经济调度方面的很多研究其目标函数只考虑了运行成本，如文献[4，5]，而考虑到环境污染加剧，环境效益也逐渐纳入目标函数。在多目标经济调度方面，国内外已有诸多研究。文献[6]采用线性加权法，可将多个目标函数转化成单目标进行求解，并分析了不同权重对调度结果的影响；文献[7]应用模糊优化理论，采用最大模糊满意度法将多目标经济调度问题转化成非线性单目标优化问题，采用改进遗传算法进行优化调度，并比较分析了单目标与多目标的优化结果，但这两种方法所生成的只是个别最优解，可供选择的解空间太小。文献[8]采用NSGA—II算法，综合考虑了运行成本和污染物排放两个目标函数，依托 IEEE—30和IEEE—118节点系统进行算例试验，并将结果与采用实数编码的遗传算法得到的结果进行比较，表明算法的良好性能。但微网与IEEE标准测试系统有很大不同，而电动汽车的接入，更加大了这种差别。文献[9]基于NSGA—II算法，考虑了燃料成本最低，二氧化硫排放最少，氮氧化物排放最少等三个目标函数进行经济调度，但就污染而言，二氧化硫与氮氧化物可以统一考虑，而考虑到温室效应减少碳排放，应当考虑二氧化碳排放最少作为目标函数之一。

因此，本文在电动汽车数学模型基础上，综合考虑微网系统运行成本最低、二氧化碳排放最少、污染物处理费用最低三个目标函数，采用NSGA—II算法对目标函数间的关系进行分析，然后采用优先顺序法对含电动汽车的微网系统经济调度进行算例仿真，并分析电动汽车入网及负荷波动的影响。

2 电动汽车的数学建模

2.1 电动汽车时空特性建模

本文电动汽车建模的对象主要是私家车。空间特性主要是考虑车主的行驶习惯[10]，简单理解为日行驶里程问题；时间特性主要是考虑电动汽车的行驶结束时刻，假设车主都在行驶结束后开始充电，则为起始充电时刻。

据统计[11]，电动汽车日行驶里程S近似满足对数正态分布，即，其概率密度函数为

电动汽车的最后一次返程时刻 t0服从正态分布，即，其概率密度函数为

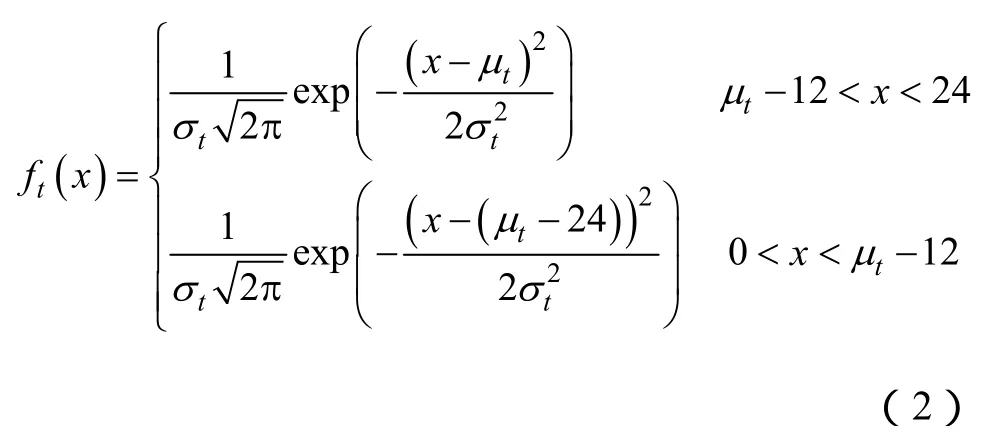
式中， μs= 8 .92；σs= 3 .24； μt=17.47；σt=3.41。

本文假设每辆电动汽车充放电均以常规慢速方式进行，功率在2～3kW间均匀分布。电动汽车参数见附录A表A1。通过蒙特卡洛模拟法，由式（1）可得电动汽车的日行驶里程S，由式（2）可得电动汽车最后一次返程时刻 t0，即入网充电起始时刻。

2.2 电动汽车的无序充电模型

电动汽车无序充电，是指在政府部门未采取相关政策时，用户均自主对电动汽车进行充电的充电模式。

由日行驶里程 S、百千米耗电量 W100、充电功率PC和充电效率ηC_EV便可通过式（3）得到电动汽车的充电持续时长，公式如下

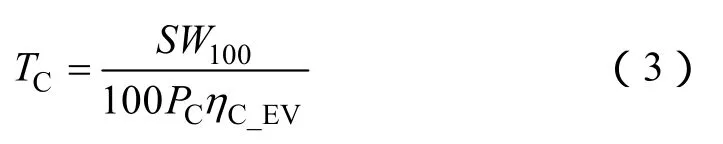
对于每辆电动汽车，由入网起始充电时刻和充电持续时长便可得到充电结束时刻。则累计各时段充电功率即可得总充电负荷。因为各辆电动汽车的充电时间相互独立，则可通过蒙特卡洛模拟法，计算得到大量电动汽车充电的日负荷表达式为

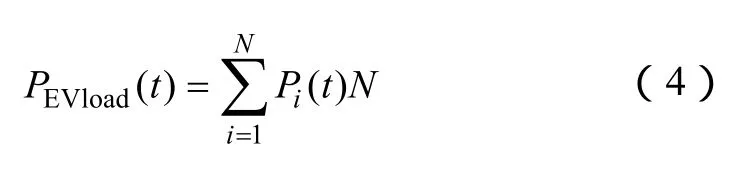
式中， PEVload(t)为时刻t的总充电功率，t= 1 ,2,··,2 4 ；N为电动汽车的数量；Pi( t)为第i辆电动汽车在时刻t的充电功率。

当调度周期为一天时，不同规模的电动汽车无序充电的日负荷曲线如图1所示。

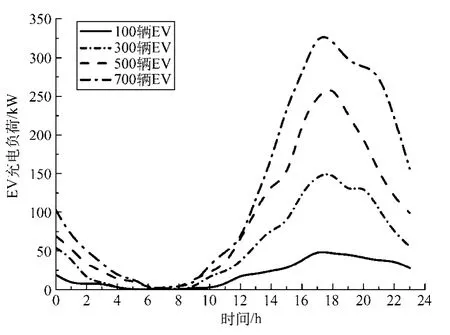
图1 不同规模EV无序充电模式下日负荷曲线图Fig.1 The load curve of different scale EVs under the uncoordinated charging mode

由图1可看出，电动汽车数量越多，负荷峰值越高。电动汽车无序充电的负荷主要集中在18点左右，正是下班高峰，用户一般在下班回家后开始给电动汽车充电。仿真结果与用户行为相符。

2.3 电动汽车的有序充放电模型

电动汽车有序充放电，即采用V2G方式入网，是在电价引导等政策下，在满足车主使用习惯条件下，对电动汽车充电和放电进行集中有序控制。为研究方便，认为其完全服从有序充放电调度。即负荷低谷时，电动汽车作为负荷充电；负荷高峰时， 电动汽车作为电源，放电供其他负荷使用。

由电动汽车蓄电池荷电状态（SOC）约束、日行驶里程S和放电功率 PdisC，可以得到最大放电持续时间为

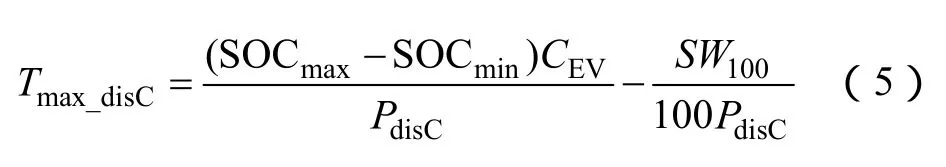
式中， CEV为电动汽车电池的总容量。入网放电时刻由最后一次返程时刻 t0与负荷高峰配合得到。放电结束时刻由最大放电时间与调度周期配合得到，即截止时间为 24点。两者相减即为实际放电时间TdisC，在此期间，电动汽车放电。将N辆电动汽车的放电功率累加起来，便可得到放电时段内电动汽车的总放电功率。

单辆电动汽车充电时所需电量为一天中所耗总能量，包括日行驶耗电量和日放电量，可采用下式计算

WEV除以充电功率及充电效率，可得充电持续时间 TC，公式如下

则用式（4）所述方法累加，即可得到充电时段的总充电功率。

电动汽车有序充放电的负荷曲线如图2所示。正值表示电动汽车充电，负值表示电动汽车放电。

由图2可看出，电动汽车充电负荷主要集中在0～6时段，处于夜间负荷低谷阶段，避开了负荷高峰，有利于微网稳定，且此时电价较低，对车主来说经济性较好；6～16时段，电动汽车主要作为交通工具使用，且此时也是车主用车时间；放电主要集中在16～24时段，此时是负荷高峰时间，电动汽车可以作为电源使用，参与经济调度。

3 微网系统多目标的数学模型

3.1 微网系统的多目标函数

具有n个决策变量的多目标优化的数学模型如下式所示：

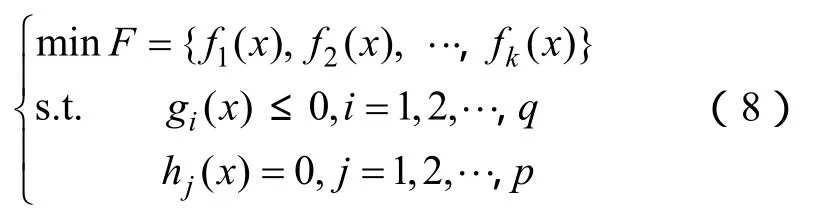
式中， x =( x1,x2,··,xn)为n维决策向量； fk(x)为第k个目标函数； gi( x)≤ 0 为q个不等式约束条件；hj( x) = 0 为p个等式约束条件。

本文多目标经济调度考虑微网系统的运行成本C1最低、二氧化碳处理费用 C2最低、污染物处理费用 C3最低等三个目标函数。

（1）目标函数1：系统运行成本最低

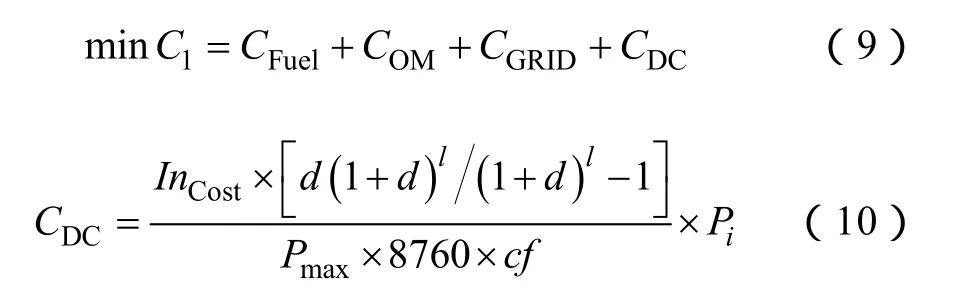
式中，CFuel为发电单元燃料消耗成本（元）；COM为发电单元的运行管理成本（元）； CGRID为微网与大电网交互成本（元），正值代表系统从大电网吸收功率，负值代表系统向大电网输送功率； CDC为发电单元折旧成本（元）； Pmax为发电单元的最大输出功率（kW）； Pi为发电单元i发出的电量（kW）；cf为容量因素； I nCost为发电单元单位容量安装成本（元）；d为利率，取8%；l为发电单元寿命（年）。各发电单元费用参数见附录A表A2。

（2）目标函数 2：二氧化碳的排放最少，以二氧化碳处理费用最低表示

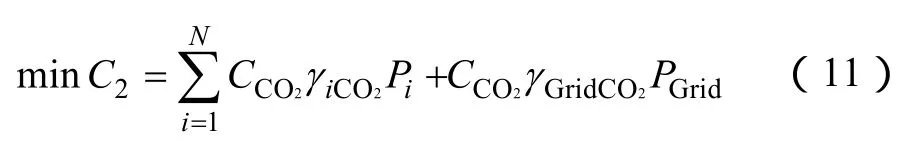
式中，N为发电单元的数目；CCO2为处理每千克二氧化碳的费用；γiCO2为发电单元i输出每千瓦电能时二氧化碳的排放系数（kg/kW）；γGridCO2为大电网输出每千瓦电能时二氧化碳的排放系数（kg/kW）；PGrid为微网与大电网间的传输功率（kW）。

（3）目标函数3：污染物处理费用最低

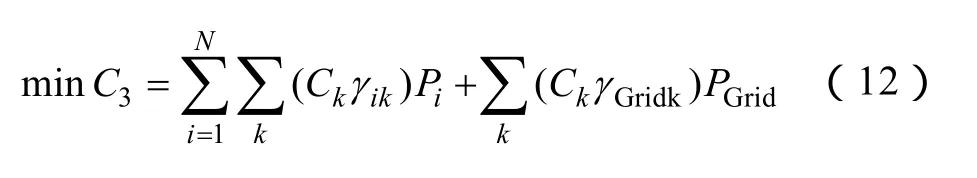
式中，k为污染物类型（ S O2、 N Ox等）； Ck为处理每千克k类污染物的费用；γik为发电单元i输出每千瓦电能时第k类污染物的排放系数；γGridk为大电网输出每千瓦电能时第k类污染物的排放系数（kg/kW）。

二氧化碳及污染物的排放系数及处理费用见附录A表A3。

3.2 约束条件

（1）功率平衡约束

式中， PGrid为正表示电网向微网输送的功率，为负表示微网向电网输送的功率； PLoad为常规负荷需求； PEVload为电动汽车的充电功率，若电动汽车处于充电状态，则为正，处于放电状态，则为负。

（2）微网内发电单元的功率限制

式中， Pimin为出力下限； Pimax为出力上限。

（3）电动汽车蓄电池的荷电状态约束

蓄电池的循环充放电次数及放电深度会影响其寿命，因此要对其荷电状态（SOC）进行约束

式中，SOC(t)为t时刻的荷电状态； S OCmin为荷电状态下限，本文取做0.2； S OCmax为荷电状态上限，本文取做0.8。

（4）微网与大电网间联络线传输容量约束

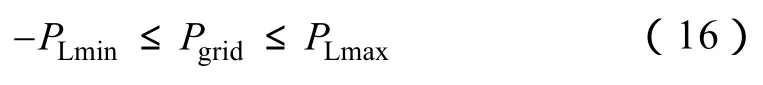
式中， PLmin为微网向电网输送功率下限； PLmax为电网向微网输送功率上限。

4 NSGA-II算法的多目标函数分析

4.1 NSGA-II算法

自从意大利经济学家V.Pareto提出多目标最优化问题，引进Pareto最优概念后，学界对此展开了多方研究。2000年，Deb等人改进了NSGA算法（非支配排序遗传算法），提出了NSGA—II算法[12]（带精英策略的快速非支配排序遗传算法），可以较好地解决多目标优化问题[13]。

本文中经济调度的目标函数有三个：运行成本最低、二氧化碳处理费用最低和污染物处理费用最低。则需要研究三个目标函数间的关系，因为若两个目标互斥，则不能同时达到最优，故需要进行折中；若不互斥则能同时达到最优，可以合并为单目标。故此，本文采用NSGA—II算法多目标函数分析，对应的流程图如图3所示：

如图3所示，NSGA—II算法描述为：首先，随机产生规模为N的初始种群 Pn，经过选择、交叉、变异产生子代种群 Qn，将两个种群合并成规模为2N的种群 Rn；然后对 Rn中的个体进行快速非支配排序形成一系列非支配层，对每个非支配层中的个体进行拥挤度计算并排序，选取前N个个体形成新的父代种群 Pn+1；重复以上步骤直至程序循环结束。

图3 NSGA—II算法的流程图Fig.3 Flowchart of NSGA—II

4.2 多目标函数算例结果及分析

本文的微网系统包含风力发电机、光伏阵列、柴油机、燃料电池等分布式电源和电动汽车。风电机组10组，太阳能电池板30块；柴油机和燃料电池的数量皆为 2组，单组功率上限为 30kW；可入网电动汽车有80辆。系统采用并网运行方式，电动汽车采取无序充电和有序充放电两种模式，考虑最大化利用可再生能源的运行策略，调度周期为1天，分为24时段分别进行计算。在Matlab环境下编程，应用 NSGA—II算法，种群大小 100，最大迭代次数200，交叉概率0.9，变异概率0.1。

下面以时刻 15为例，分析多目标函数间的关系。常规负荷 134.706kW，光伏单元发电功率16.79kW，风机发电功率 31.00kW，电网实时电价0.754 1元/kWh。得到的电动汽车无序充电及有序充放电时的Pareto最优解前沿如图4所示。

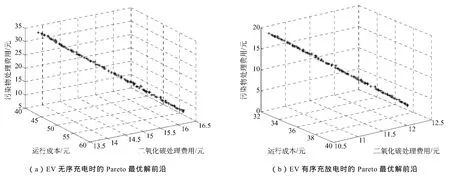
图4 EV不同充放电模式下的Pareto最优解前沿Fig.4 Pareto-optimal front of EVs under different charging/discharging mode

由图4可以直观地看出，运行成本随二氧化碳处理费用增加而增加，则两者可以同时达到最优；而两者费用都增加时，污染物处理费用下降，则运行成本、二氧化碳处理费用都与污染物处理费用之间互斥，不能达到同时最优。按线性加权法等常规多目标优化模型得出的调度结果只有一组最优解，则不能完善地权衡互斥目标间的关系。本文 NSGA—II算法结果是得到一个最优解集，各个最优解均匀地分布在Pareto前沿上，保证了最优解的多样性，微网运行者可以根据当地需要在最优解集中进行选择，权衡微网运行成本、二氧化碳排放和环境效益。

若负荷全由大电网供电，在时刻15，电动汽车无序充电时，计算可得运行成本（购电费用）为86.63元，图4a中运行成本坐标轴值皆低于此费用，则可看出此时微网的经济性较好。二氧化碳处理费用为21.45元，图4a中二氧化碳处理费用坐标轴值皆低于此费用，说明此时微网二氧化碳排放量较少。污染物处理费用为14.64元，与图4a中污染物处理费用坐标轴值比较， Pareto最优解集中一部分解高于此值，这是因为此时柴油机出力较多，而其污染较大。

同理，电动汽车有序充放电时，计算可得运行成本（购电费用）为 69.30元，二氧化碳处理费用为17.14元，污染物处理费用为11.69元，与图4b中各坐标轴值比较，也可得到上述结论。

5 含电动汽车的微网系统经济调度

5.1 基于模糊逻辑理论的多目标函数处理

本文第4节应用NSGA—II算法只可进行单点多目标调度，虽效果良好，但由于得到的是最优解集，相邻两时刻难以配合，故不能实现连续调度。

因此，本节从最优解集中选取一组最优解进行微网系统的连续经济调度。考虑到运行成本 C1和二氧化碳处理费用 C2并不互斥，可同时达到最优，故合并为一个目标，与污染物处理费用 C3组合，基于模糊逻辑理论[14]，将他们视为同等重要的决策目标，采用线性加权法即可将多目标函数转化为模糊单目标函数C

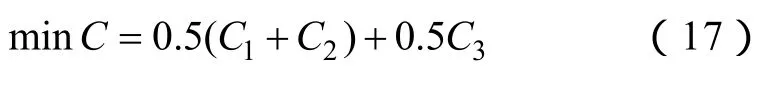
5.2 微网系统经济调度的优先顺序法

优先顺序法是将系统中分布式电源按所要求的目标函数费用由小到大排序，根据负荷大小，依次投入发电。多时段的决策过程一般收敛较慢或难于收敛，而优先顺序法把多时段的最优问题简化为各时段的最优问题逐一解决，减少了计算量，且计算过程简便、高效。由于它是在每一个时段内对目标函数进行最优求解，所以它的所有时段的总和必然也是全局的最优解。

5.3 微网系统的调度控制策略

调度策略 1：微网并网运行，电动汽车无序充电。不考虑电动汽车的放电特性，即负荷（常规负荷+电动汽车充电负荷）由燃料电池、柴油机、大电网按优化调度结果来出力。

调度策略 2：微网并网运行，电动汽车有序充放电。在大电网电价低谷时，利用低电价给电动汽车充电，将电能储存于电动汽车电池中，以备在电价高峰时使用，负荷（常规负荷+电动汽车充电负荷）由可再生能源和大电网供电；电价高峰时段电动汽车为高峰负荷放电，负荷（常规负荷减去电动汽车放电负荷）由燃料电池、柴油机、大电网按优化调度结果来出力；平价时段电动汽车作为交通工具，负荷（常规负荷）由燃料电池、柴油机、大电网按照优化调度结果来出力。并网时电动汽车在放电时段内全部放电。

5.4 不同调度策略下各分布式电源的出力分析

微网系统经过经济调度后，各分布式电源和大电网的出力结果如图5所示。

图5 不同调度策略下各发电单元出力情况Fig.5 Generating unit output under different strategies

当微网系统采用调度策略1时，从图5a可以看出：在0～2时段，风机输出功率较大，而微网总负荷较小，则微网将多余电力输送至大电网。所以在图5a中，0～2时段大电网出力为负值。至时刻3，可再生能源出力不足以满足负荷需求，考虑到燃料电池综合成本较低，则启用燃料电池。时刻5以后，燃料电池因为综合成本低于柴油机及大电网，所以一直按最大出力发电。7～10时段，大电网综合成本低于柴油机，则与燃料电池一同出力。至时刻11，大电网综合成本高于柴油机，则柴油机代替大电网与燃料电池一同出力。时刻15以后，柴油机综合成本又高于大电网，则停用，负荷改由燃料电池、大电网供电。

当微网系统采用调度策略2时，从图5b可以看出：电动汽车充电负荷集中在0～5时段，这时大电网、燃料电池的综合成本低于柴油机，则一同出力供电。燃料电池以其综合成本较低，此后一直优先使用。6～16时段，电动汽车不参与调度，其中7～10时段大电网综合成本低于柴油机，则与燃料电池一同出力。11～14时段，柴油机综合成本较低，代替大电网与燃料电池一同供电。时刻15以后柴油机综合成本高于大电网，则停用。至时刻17，电动汽车开始放电，参与调度，与燃料电池、大电网一起为负荷供电。

5.5 不同调度策略下各目标函数的费用分析

在不同调度策略下，各目标函数的费用及总费用如表1所示。

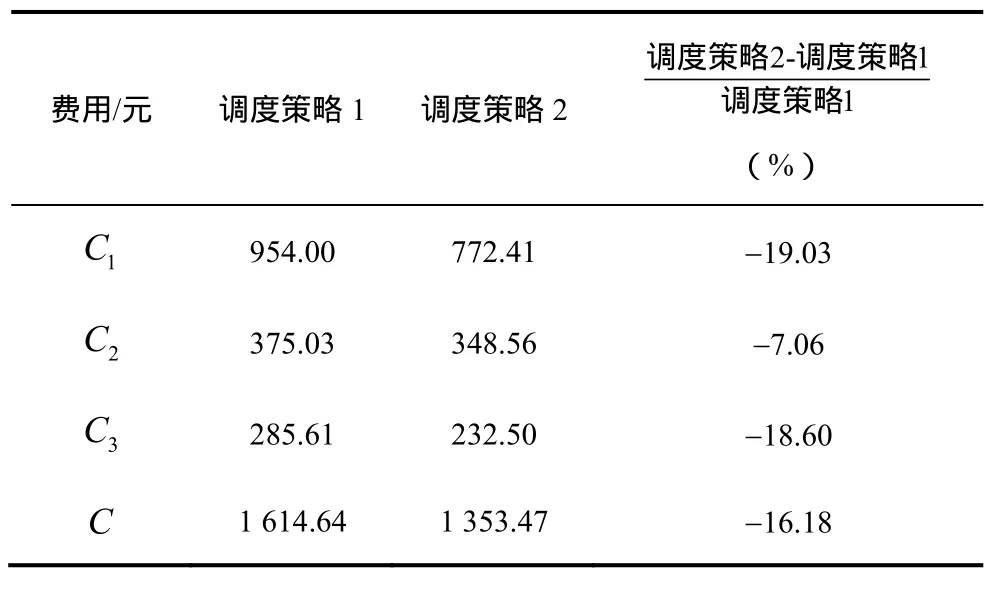
表1 不同调度策略下的调度结果费用Tab.1 Cost of dispatch results under different strategies

比较表中数据可看出，微网系统采用调度策略2时的各项费用比采用调度策略 1时的各项费用，分别降低了19.03%，7.06%，18.60%和16.18%，这说明当电动汽车以有序充放电的方式入网时，在总体的经济性、运行成本、二氧化碳排放、污染物排放等方面都有更好优势。并且，比较图5a和图5b可以看出，电动汽车在夜间电价低谷时充电，避开了负荷高峰，而在负荷高峰时放电，则可以减少向大电网购电的费用。这样，利用电动汽车的充放电控制，不仅实现削峰填谷，还降低了微网系统的总体费用，有利于提高系统的经济性。

5.6 负荷的不确定性对经济调度的影响分析

研究表明，电力系统的负荷波动一般可以用正态分布进行描述[15]。其概率密度函数如下

式中，δL为负荷预测的标准差；PLf为负荷预测值；PL为实际负荷值。

在微网系统经济调度过程中，为保证运行的可靠性，负荷波动的不确定性可以通过一定的旋转备用来平抑，本文研究过程中旋转备用由大电网提供。

表2 不同负荷波动情况下调度结果总费用Tab.2 Total cost of dispatch results under different load fluctuation

从表2中的数据可以直观地看出，无论是在调度策略1还是调度策略2情况下，随着负荷波动的增加，微网运行的总费用都增加。因为负荷波动越大，微网所需要的旋转备用容量就越多，则向大电网购电所需的费用就越高，则运行总费用也越高。

此外，在负荷波动相同的情况下，电动汽车在有序充放电时的总费用都低于无序充电时的总费用。表2中，当负荷不确定性参数从0%分别增加到5%、10%、15%和20%时，电动汽车采取有序充电时比无序充电时的总费用分别降低了15.97%、15.77%、14.21%、12.16%，仿真结果与5.5节的分析相一致。

6 结论

根据电动汽车的时空特性，建立了电动汽车无序充电和有序充放电的负荷模型。基于多目标优化模型及微网经济调度研究现状，确定了运行成本最低、二氧化碳排放最少和污染物处理费用最低三个目标函数，计及安全运行约束条件，建立了含电动汽车的微网系统多目标经济调度模型。基于 NSGA—II算法分析了多目标函数间的关系，最优解均匀地分布在Pareto最优解前沿上，保证了最优解的多样性。最后，将多目标函数处理为单目标函数，采用优先顺序法，基于不同的调度控制策略，对含电动汽车的微网系统进行经济调度，验证了模型和算法的正确性。仿真结果表明，电动汽车通过有序充放电入网比无序充电入网具有较高的经济性，与此同时，负荷波动越大，微网系统运行总费用越高。

附录A 系统参数

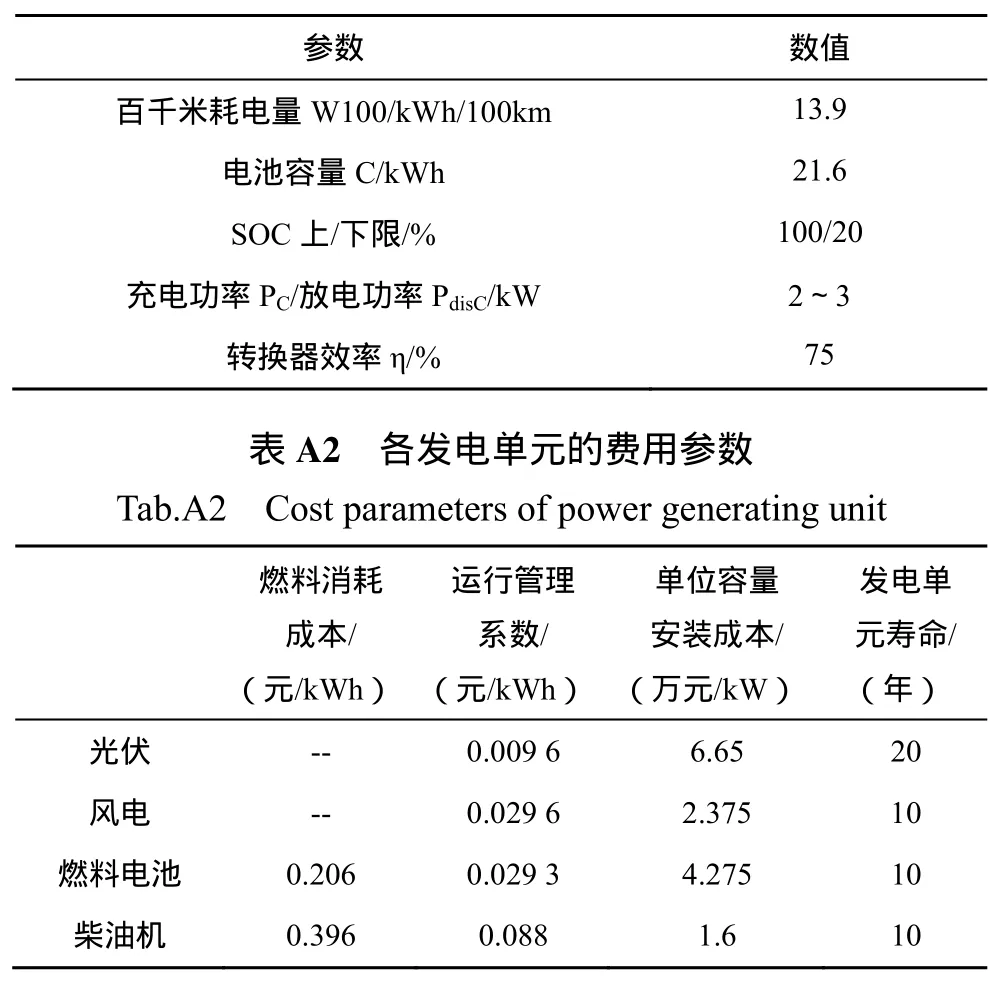
表A1 电动汽车的参数Tab.A1 Parameters of Electric vehicle

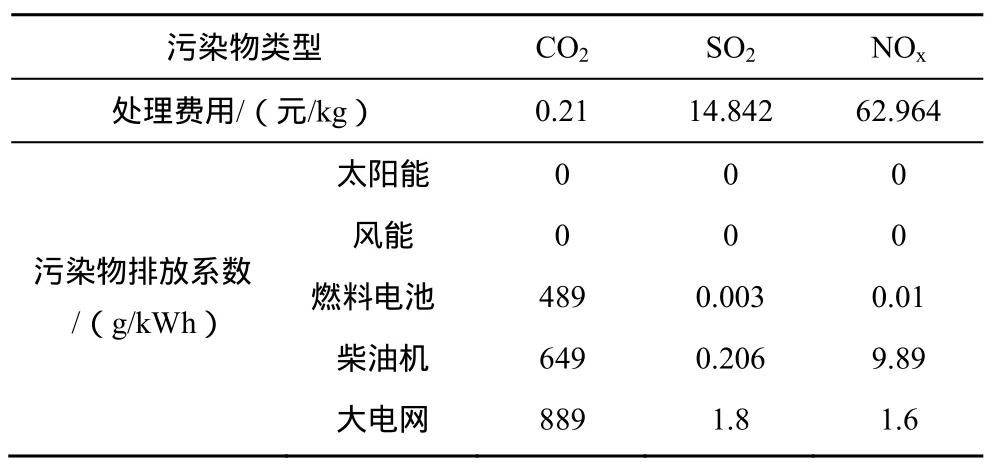
表A3 二氧化碳和污染物排放系数Tab.A3 Parameters of carbon dioxide and pollutant emissions

图A1 可再生能源发电输出功率Fig.A1 Output of renewable energy generation

图A2 微网系统的负荷需求Fig.A2 Load demanding of microgrid system

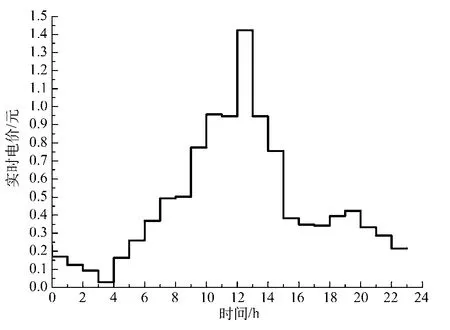
图A3 电网实时电价Fig.A3 Electricity price of grid

[1] 高赐威,张亮.电动汽车充电对电网影响的综述[J].电网技术,2011,35(2): 127-131.Gao Ciwei,Zhang Liang.A survey of influence ofelectrics vehicle charging on power grid[J].Power System Technology,2011,35(2): 127-131.

[2] Kempton W,Tomić J.Vehicle-to-Grid power fundamentals: calculating capacity and net revenue[J].Journal of power sources,2005,144(1): 268-279.

[3] 肖湘宁,陈征,刘念,等.可再生能源与电动汽车充放电设施在微电网中的集成模式与关键问题[J].电工技术学报,2013,28(2): 1-14.Xiao Xiangning,Chen Zheng,Liu Nian,et al.Integrated mode and key issues of renewable energy sources and electric vehicles' charging and discharging facilities in microgrid[J].Transactions of China Electrotechnical Society,2013,28(2): 1-14.

[4] 蒋秀洁,徐满清,龚学会,等.计及阀点效应负荷经济分配的杂交粒子群算法[J].电力系统保护与控制,2009,37(8): 10-13.Jiang Xiujie， Xu Manqing， Gong Xuehui,et al.Hybrid particle swarm optimization for economic dispatch with valve-point effect[J].Power System Protection and Control,2009,37(8): 10-13.

[5] 修春波,陆丽芬.改进的混沌优化算法及其在电力系统负荷分配中的应用研究[J].电力系统保护与控制,2010,38(21): 109-112,117.Xiu Chunbo,Lu Lifen.Chaos optimization algorithm and its application in economic load dispatch on power system[J].Power System Protection and Control,2010,38(21): 109-112,117.

[6] Mohamed F A,Koivo H N.Online management of microgrid with battery storage using multiobjective optimization[C].Power Engineering,Energy and Electrical Drives,2007.POWERENG 2007.International Conference on.IEEE,2007: 231-236.

[7] 陈洁,杨秀,朱兰,等.微网多目标经济调度优化[J].中国电机工程学报,2013,33(19): 57-66.Chen Jie,Yang Xiu,Zhu Lan,et al.Microgrid multi-objective economic dispatch optimization[J].Proceedings of the CSEE,2013,33(19): 57-66.

[8] Rajkumar M,Mahadevan K,Kannan S,et al.NSGA-II technique for multi-objective generation dispatch of thermal generators with nonsmooth fuel cost functions[J].Journal of Electrical Engineering &Technology,2014,9(2): 423-432.

[9] King R T F A,Rughooputh H C S.Elitist multiobjective evolutionary algorithm for environmental/economic dispatch[C].Evolutionary Computation,2003.CEC'03.The 2003 Congress on.IEEE,2003,2: 1108-1114.

[10] 吴红斌,侯小凡,赵波,等.计及可入网电动汽车的微网系统经济调度[J].电力系统自动化,2014,38(9): 77-84.Wu Hongbin,Hou Xiaofan,Zhao Bo,et al.Economical dispatch of microgrid considering plug-in electric vehicle[J].Automation of Electric Power Systems,2014,38(9): 77-84.

[11] Vyas A,Santini D.Use of national surveys for estimating ‘full’ PHEV potential for oil use reduction[EB/OL].http://www.transportation.anl.gov/pdfs/HV/525.pdf,2008.

[12] Ahmed F,Deb K.Multi-objective optimal path planning using elitist non-dominated sorting genetic algorithms[J].Soft Computing,2013,17(7):1283-1299.

[13] 李莉.基于遗传算法的多目标寻优策略的应用研究[D].无锡: 江南大学,2008.

[14] 周明,娄雅融.兼顾购电费用和煤耗的双目标加权模糊发电调度模型[J].电网技术,2010,34(11):140-145.Zhou Ming,Lou Yarong.A bi-objective weighted fuzzy generation dispatching model considering both power purchase cost and coal consumption[J].Power System Technology,2010,34(11): 140-145.

[15] 刘小平,丁明,张颖媛,等.微网的动态经济调度[J].中国电机工程学报,2011,31(31): 77-84.Liu Xiaoping,Ding Ming,Zhang Yingyuan,et al.Dynamic economic dispatch for microgrids[J].Proceedings of the CSEE,2011,31(31): 77-84.