双余度永磁无刷直流电机匝间短路故障诊断

付朝阳 刘景林 张晓旭

（西北工业大学自动化学院 西安 710072）

1 引言

在航空航天等高精密控制系统中，广泛采用余度控制技术。控制系统中实现余度控制一种方案是一台电机及其控制系统作为一个通道，采用多台电机及其控制系统并联运行，这种方案的缺点是体积大、重量重、成本高。另一种方案是将余度技术引入到电机上，电机定子中设置多套绕组，共用一套转子系统，每套绕组分别与控制系统构成独立的通道。该方案特点是体积小、重量轻、成本低。

目前，国内科研机构已对多绕组电机进行了一些研究[1]，而对双余度电机的研究较少。文献[3]研究了双余度无刷直流电机的极弧系数对其转矩波动的影响，通过采用电磁场有限元分析的方法，计算了极弧系数对电气双余度波形和定位转矩的影响，给出了电气双余度极弧系数选取的参考方法。文献[4]采用场路结合的方法设计了一种用于直接驱动作动器（DDA）的电气/机械混合式四余度无刷直流力矩电动机，该电机具有同轴的两段定、转子，每段定子中隔槽嵌放两套绕组，从而构成电气/机械混合四余度，通过实验验证了该方案的可行性。文献[5]对双余度无刷电机的数学模型进行了推导，设计了相关原理样机，验证了双余度设计的可行性。文献[7]研究了绕组短路故障对直接驱动作动器（DDA） 用电气/ 机械混合四余度无刷直流力矩电动机（BLDCTM） 性能的影响，分析了短路故障对电机电气参数造成的影响，系统的仿真结果表明某一相绕组出现匝间短路或某余度的两相绕组出现相间短路时，系统依然可以正常运行，大大提高了系统的可靠性。文献[8]针对航空电作动系统用双余度无刷直流电机的方案寻优问题，提出了一种基于遗传算法的优化设计方法，计算结果表明：在满足性能要求的前提下，优化设计能够有效地减小系统的体积重量。

在上述文献中，大多针对双余度永磁无刷直流电机的设计及其控制方法进行了研究，针对故障诊断方面的研究较少。由于绕组中设置了两套绕组，大大提高了系统的可靠性，但是作为一个多源故障系统，双余度永磁无刷直流电机由于绕组间的耦合作用，存在一个故障对应多个故障特征和多个故障特征对应相似故障特征的情况，并且由于早期绕组匝间短路故障信号微弱而难以被发现。对于中小型的永磁直流电机，绝缘良好的漆包线漆膜可承受4 000V的高压，而正常情况下，电机工作电压不超过400V，因此绝缘未受损坏的电机在应用中发生匝间短路的可能非常小。但由于电机在生产和安装过程中，经过绕线、嵌线、排线和多次搬运，每道环节都可能使线圈导线的漆膜划伤或擦伤；另一方面，电机在应用中由于频繁停、转等操作而引起的电枢回路过电压，使绕组绝缘薄弱处的绝缘击穿，也极易形成绕组匝间短路。

2 匝间短路仿真模型的建立与求解

2.1 故障信号的选择

双余度永磁无刷直流电机采用了两套电枢绕组，在电机运行时，两套绕组会通过电感互相耦合，而当电机发生故障时，电机的转速、转矩和电流等都会发生变化，电机转矩方程如下所示：

式中 CT——转矩常数；

φ——每极磁通；

I——电枢电流。

设电枢电流的脉动频率为，可知电机转速为

式中 n——电机转速；

p——电机极对数。

由上述两个公式可以看到，其转矩、转速均与电流相关。因此当电机发生故障时，电机的电枢电流信号会有比较明显的变化，主要表现在以下几个参数中：稳态电枢电流均值，稳态电流的基波频率等。

2.2 仿真模型的建立

随着科学技术的进步，飞行器电源系统也在不断发展。在经历了低压直流电源、恒速恒频（CSCF）交流电源、变速恒频（VSCF）电源之后，未来飞行器中将会采用高压直流电源系统，基于此，本文设计电机参数见表1。

表1 双余度高压无刷直流电机主要参数Tab.1 Main parameters of dual redundancy high voltage brushless DC motor

对于比较明显的多匝短路时，电流值会发生明显突变，而对于细微的匝间短路时，普通的电流检测则很难发现，为了能够准确地模拟短路故障，本文将其中的一相定子槽分为两部分，短路的部分匝数为5，如图1所示（3、6、9、12点方向的定子槽被分为两部分），这两部分分别嵌入线圈，保持总的匝数不变（与其他定子槽匝数一致）。

图1 匝间短路仿真模型Fig.1 Simulation model of inter-turn short circuit

2.3 仿真结果

采用 3D瞬态求解器进行计算，得到一余度 A相匝间短路时各相电流波形，如图2所示。与正常模型仿真和实验值相比，各相电流均略有增加。

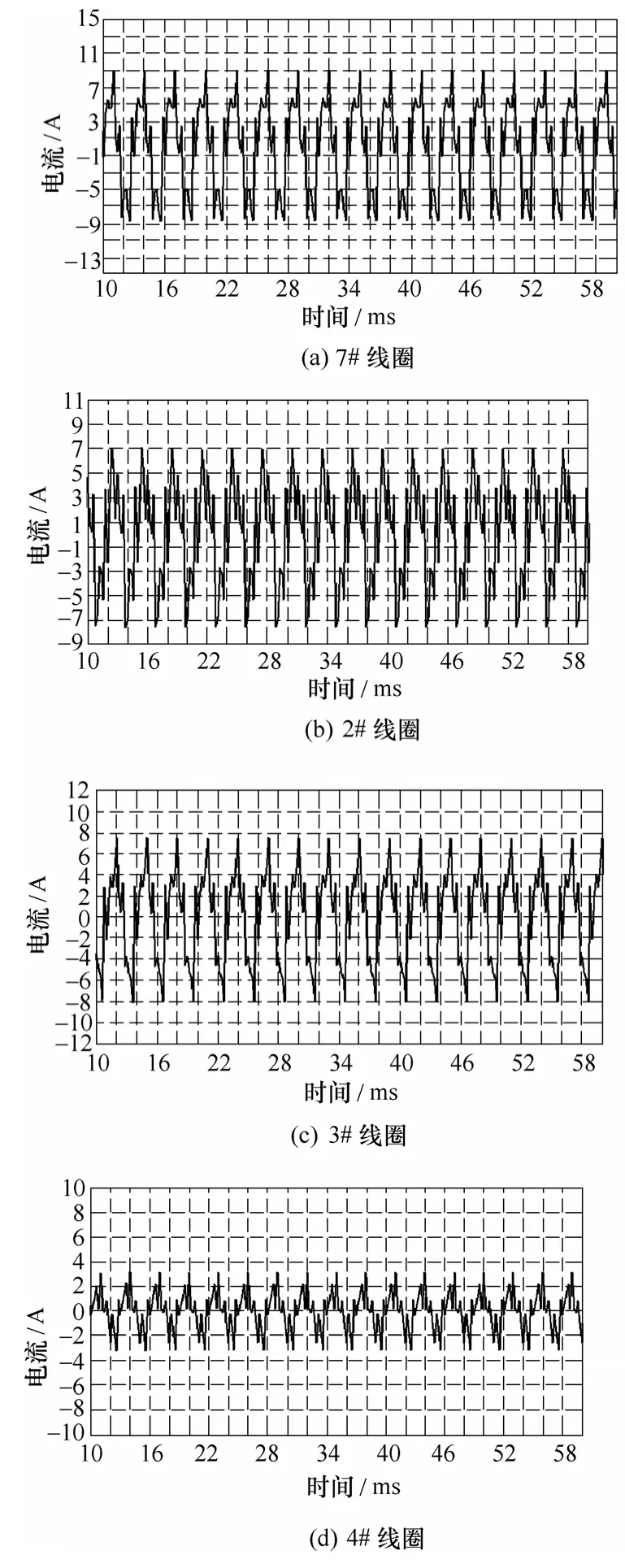
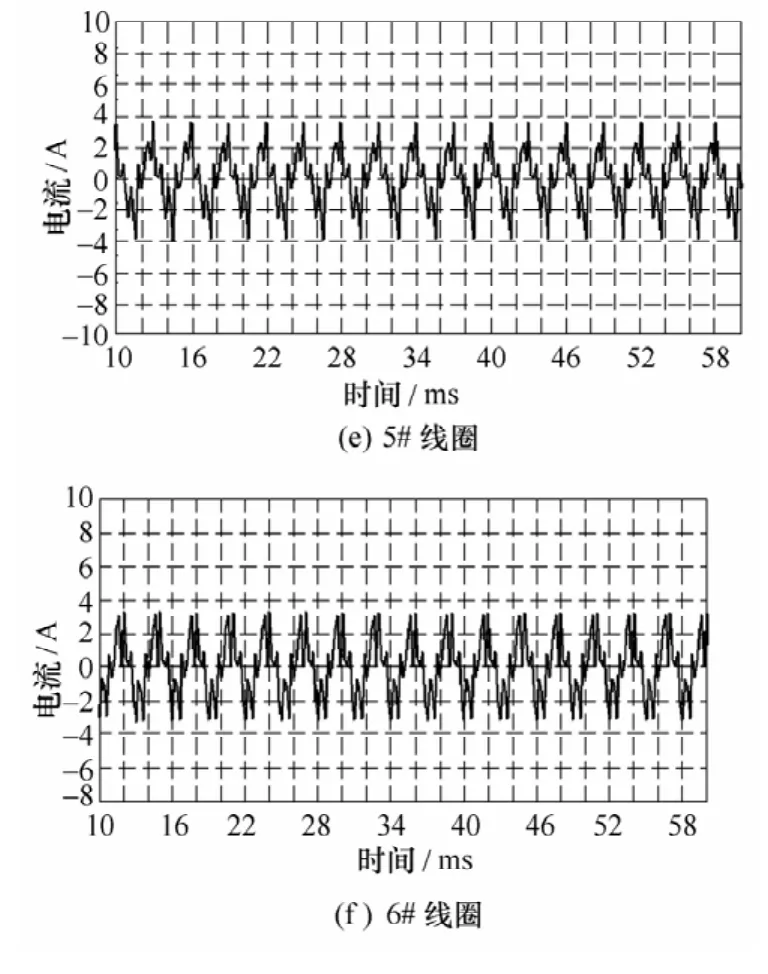
图2 相电流波形Fig.2 Phase current waveform

3 故障信号特征提取

3.1 小波函数的选择

由于小波函数具有多样性，对于同一信号进行信号处理选用不同的小波基波，得到的结果往往差别很大，小波分析在工程应用中的一个十分重要的问题就是选择最优小波基问题。目前主要是通过用小波分析方法处理信号的结果与理论结果的误差来判定所选小波基的好坏，并由此选定小波基[14,15]。

考虑电流信号 X = { xk| xk∈ R }k∈Z，把X分成二个不相交的集合：偶下标采样 Xe= { x2k}k∈Z和奇下标采样 Xo={x2k + 1 }k∈Z，通常情况下这两个集合是紧密相关的，因而从一个集合能很好地建立另一个集合的预测P。

知道了d和奇采样值，可立即恢复信号

若P性能好，则d将是一个稀疏集，换言之，期望d的一阶熵小于xo的。

取 λ-1,k= λ0,2k,k ∈ Z

利用相邻两偶采样对奇采样进行预测，记差值

若信号是相关的，则大多数小波系数γ-1,k将很小。在理论上，可以继续通过对{λ-1,k}k∈Z施加以上操作，然而，上述简单的操作性能并不好，为此引入另一个条件，即希望,jkλ系数的平均值在每一次分解时保持一致，或者说使，可通过借助于1,kγ-对1,kλ-进行提升来实现这点

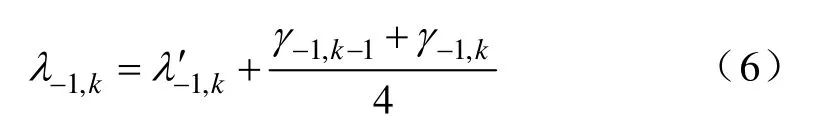
根据上述方法，本文选择了 Daubechies3和coif5小波函数进行故障信号特征提取。为了比较两种小波函数的优劣，首先对电机进行了动态仿真，在250ms时，破坏控制电路为一相5匝绕组短路，分别采用Daubechies3和coif5对一余度A相电流信号进行了2层小波分解，结果如图3和图4所示。

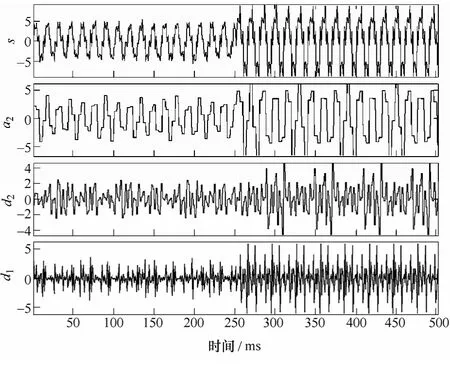
图3 Daubechies3小波分解Fig.3 Daubechies3 wavelet decomposition

图4 Coif5小波分解Fig.4 Coif5 wavelet decomposition

由仿真结果可以看到，在小波分解高频部分的第1层和第2层，250ms时明显发生了突变信号，相比较而言，coif5小波函数更能反映出故障突变点，故本文选取coif5小波函数进行特征提取。

3.2 故障特征向量

相电流d2分解系数如图5所示。求每相d2层小波分解系数序列的能量，将其按照顺序排列，得到一个向量[213.91，300.12，218.32，32.18，52.54，55.49]，同样方法可以得到其他相匝间短路时特征向量，见表2。

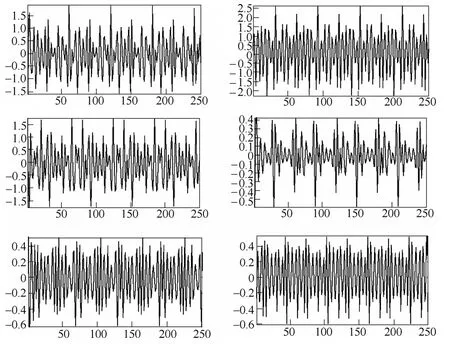
图5 d2分解系数Fig.5 d2wavelet decomposition coefficient

表2 故障特征向量表Tab.2 Fault feature vectors

4 故障模式识别

本文采用了小波分析与神经网络的松散型结合，选取小波作为信号处理的前置手段，为神经网络提供特征向量，之后完成训练和诊断。诊断模型结构如图6所示。

图6 故障诊断结构示意图Fig.6 Structure of fault diagnosis

为了便于分析，对输入样本进行归一化处理，对各故障状态能量值进行归一化后，结果见表 3，正常工作时对应于序号1，1余度A相短路时对应于序号2，以此类推。

表3 归一化后的故障特征向量表Tab.3 Normalization fault feature vectors

PNN是一种机构简单、训练简洁、应用相当广泛的人工神经网络。在实际应用中，尤其是在解决分类问题的应用中，它的优势在于用线性学习算法来完成以往非线性学习算法所做的工作。这种网络对应的权值就是模式样本的分布，故能够满足实时处理要求，本文采用PNN神经网络进行故障诊断[13]。

在进行故障诊断的过程中，求和层对模式层中同一模式的输出求和，并乘以代价因子；决策层则选择求和层中最大输出对应的故障模式作为诊断结果。当故障样本的数量增加时，模式层的神经元将随之增加。而当故障模式多于两种时，则求和层神经元将增加。所以，随着故障经验知识的积累，概率神经网络可以不断横向扩展，故障诊断的能力也将不断提高。基于PNN的系统模型如图7所示。

采用30个故障样本对PNN网络进行训练，然后采集一组测试样本，输入到PNN诊断模型中，诊断结果见表4，PNN诊断模型能够针对不同相的短路故障进行准确的诊断。

图7 PNN诊断模型Fig.7 Diagnosis model

表4 诊断结果Tab.4 Diagnosis result

5 实验

对一台双余度永磁无刷直流电机的一套定子绕组进行了改动，引出附加抽头，附加抽头之间接入短路电阻 R，以防短路电流过大烧坏电机绕组，调节短路电阻的大小可以改变短路电流，用以模拟短路故障的严重程度。

利用数据采集系统对电机进行了匝间短路故障下的电流信号采集，得到了相应的故障特征向量，诊断结果见表 5。由结果可以看到，与仿真结果基本一致，能够准确识别绕组匝间短路故障。

表5 诊断结果Tab.5 Diagnosis result

6 结论

本文针对双余度永磁无刷直流电机中常见的绕组匝间短路故障进行了研究。针对傅立叶变换的不足，提出了用小波变换进行故障检测的方法；根据电机的故障树，确定了电流作为其故障诊断信号；通过对不同小波基函数的对比分析，选择 coif5作为小波基函数；利用Mallat算法对多种典型电机故障信号进行了检测，采用第2层分解时的高频系数d2作为特征值，得到了各种故障时的特征向量。

根据电机故障信号的特点，选择小波神经网络作为其故障诊断方法，采用了松散型的结合方法；利用小波变换采集了多组故障信号特征向量并进行了归一化处理；建立了基于PNN神经网络，诊断结果表明模型能准确地识别绕组匝间短路故障。

[1] 郝亮亮,王善铭,邱阿瑞,等.多相无刷励磁系统旋转整流器故障的仿真与识别[J].电工技术学报,2012,27(4): 138-144.Hao Liangliang,Wang Shanming,Qiu Arui,et al.Simulation and recognition for rotary rectifier fault of multi-phase brushless excitation system[J].Transactions of China Electrotechnical Society,2012,27(4):138-144.

[2] 安群涛,孙力,孙立志,等.三相逆变器开关管故障诊断方法研究进展[J].电工技术学报,2011,26(4): 135-144.An Quntao,Sun Li,Sun Lizhi,et al.Recent developments of fault diagnosis methods for switches in three-phase inverters[J].Transactions of China Electrotechnical Society,2011,26(4): 135-144.

[3] 王巍,郭宏,李艳明,等.电气双余度无刷直流电动机转子极弧系数研究[J].电机与控制学报,2009,13(6): 862-866.Wang Wei,Guo Hong,Li Yanming,et al.Research on rotor pole-arc of electrical dual-redundancy brushless DC motor[J].Electric Machines and Control,2009,13(6): 862-866.

[4] Guo Hong,Wang Wei,Xing Wei,et al.Design of electrical mechanical hybrid 4 redundancy brushless DC torque motor[J].Chinese Journal of Aeronautics,2010,2(23): 211-215.

[5] 董慧芬,周元钧,沈颂华.双通道无刷直流电动机容错动态性能分析[J].中国电机工程学报,2007,27(21): 89-94.Dong Huifen,Zhou Yuanjun,Shen Songhua.Analysis on the fault-tolerant dynamic Performance of a brushless DC motor with double channels[J].Proceedings of the CSEE,2007,27(21): 89-94.

[6] 许允之,方磊,张建文.基于最小二乘支持向量机的电机故障鉴别[J].电力系统保护与控制,2012,40(14): 63-68.Xu Yunzhi,Fang Lei,Zhang Jianwen.Motor fault identification based on least squares support vector machine[J].Power System Protection and Control,2012,40(14): 63-68.

[7] 王巍,郭宏,李艳明.电气/机械混合四余度无刷直流力矩电动机绕组短路分析[J].航空学报,2010,31(5): 975-982.Wang Wei,Guo Hong,Li Yanming.Analysis of winding short-circuit in electrical/mechanical hybrid 4-redundancy brushless DC torque motor[J].Acta Aeronautica et Astronautica Sinica,2010,31(5):975-982.

[8] 武志勇,郭宏,吕振华,等.基于遗传算法的双余度无刷直流电机优化设计.北京航空航天大学学报,2011,37(12) : 1541-1545.Wu Zhiyong,Guo Hong,Lü Zhenhua,et al.Genetic algorithm based optimal design for dual-redundancy brushless DC motor[J].Journal of Beijing University of Aeronautics and A,2011,37(12): 1541-1545.

[9] 卢胜利,陈昊,昝小舒.开关磁阻电机功率变换器的故障诊断与容错策略[J].电工技术学报,2009,24(11): 199-206.Lu Shengli,Chen Hao,Zan Xiaoshu.Fault diagnosis and fault-tolerant control strategy for power converter of switched reluctance motor[J].Transactions of China Electrotechnical Society,2009,24(11): 199-206.

[10] 杨伟,顾明星,彭静萍.证据理论在电机故障诊断中的应用[J].电力系统保护与控制,2010,38(2):63-67.Yang Wei,Gu Mingxing,Peng Jingping.Application of evidence theory in fault diagnosis for electric machine[J].Power System Protection and Control,2010,38(2): 63-67.