一维非线性薛定谔方程的性质

何红生，邹卫东，张加强

(集美大学 理学院， 福建 厦门 361021)

非线性薛定谔方程(NLS)为i∂,u+α△u+β|u|2=0，称立方Schrödinger 方程，最早主要描述非线性波的调制(即非线性波包)方程[1],描述强光在光纤中的传播[2],经过几十年的研究发展，非线性薛定谔方程成为物理学中的一个重要模型，可以描述许多物理过程，如：激光巨变、等离子体物理、非线性光学[3]、分子动力学、玻色爱因斯坦凝聚[4～6],流体力学等等。近年来，非线性薛定谔方程也是一种研究热门的非线性物理方程，并且得到很多重要又有意义的结论[7～10]。

本文我们考虑一维的非线性薛定谔在外势场中的性质，主要讨论了点电荷电势、周期势等两种外势场情况，非线性薛定谔方程有哪些具体的性质，进而讨论非线性薛定谔方程的性质受哪些因素的影响，从而可以更加清楚的去了解非线性薛定谔方程的相关性质。

一维非线性薛定谔方程的表达式为

(1)

其中，α,β可以是复数。

外势场中一维非线性薛定谔方程的表达式为

(2)

一、点电荷势场的情况

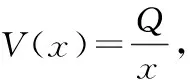
(3)

为了数值计算的方便，我们选择合适的参数α=1+i,β=1+i，Q=sin(t)

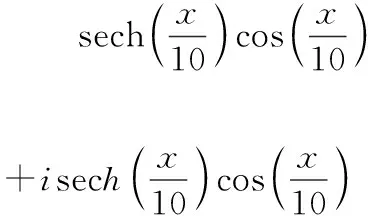
选周期性边界条件：u(-10,t)=u(-10,t)

经过数值计算，其结果如图1所示：

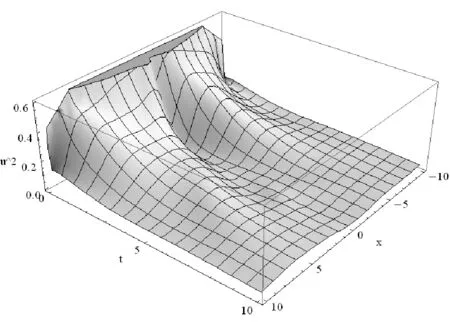
图1 |u|2与变量x,t的关系

我们研究一下振幅|u|2随时间变化的关系，对图1作不同时刻的截面图，可得：

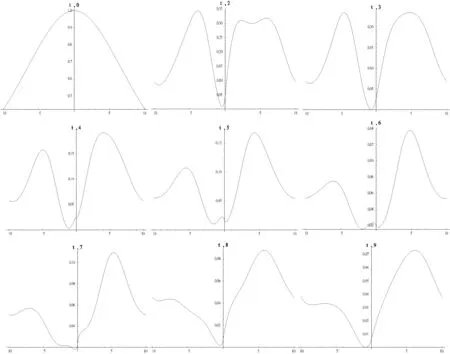
图2 |u|2与时间t的关系切片图

研究表明在点电荷势场中一维中的孤子会发生劈裂两个孤子，并且随着时间会发生改变。

二、周期势场的情况

1.正弦函数的周期势

取周期势场为：V(x)=sin(x),

则有

(4)

为了数值计算的方便，我们选择合适的参数α=1+i,β=1+i

取定初始条件：u(x,0)=sech(x)cos(x)+isech(x)cos(x)

选周期性边界条件：u(-10,t)=u(10,t)

经过数值计算，其结果如图3所示：

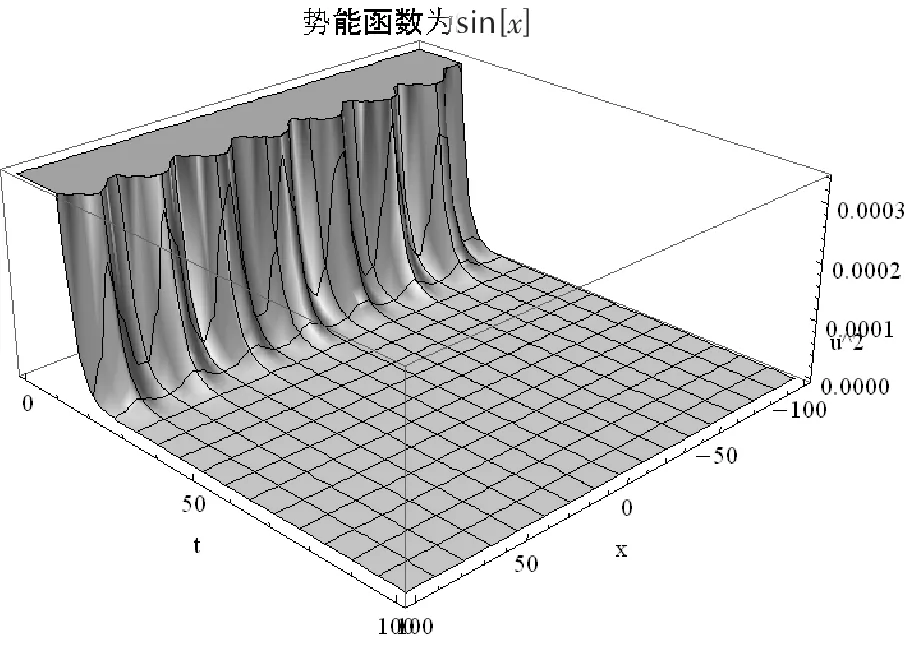
图3 |u|2与x,t的关系图

我们研究一下振幅|u|2随时间变化的关系，对图3作不同时刻的截面图，可得：

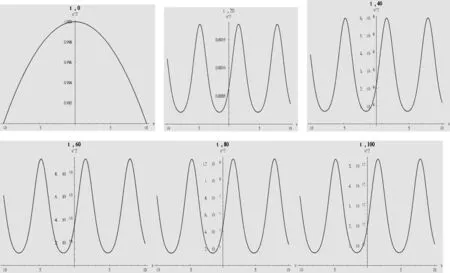
图4 |u|2与时间t的关系切片图

研究表明在正弦周期势场中非线性薛定谔方程具有较好的周期解，不过随着时间的变化周期的振幅在变小。

2.正切函数的周期势

取周期势场为：V(x)=tan(x)，

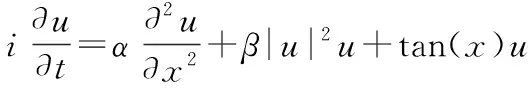
(5)

为了数值计算的方便，我们选择合适的参数α=1+i,β=1+i

取定初始条件：u(x,0)=sech(x)cos(x)+isech(x)cos(x)

选周期性边界条件：u(-10,t)=u(10,t)

经过数值计算，其结果如图5所示：

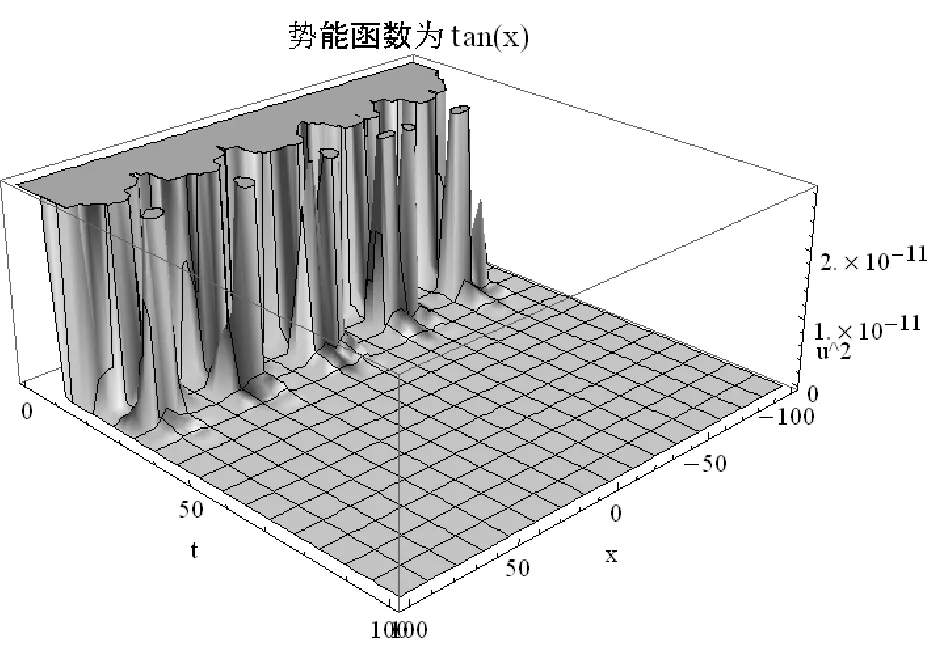
图5 |u|2与x,t的关系图

我们研究一下振幅|u|2随时间变化的关系，对图5作不同时刻的截面图，可得：

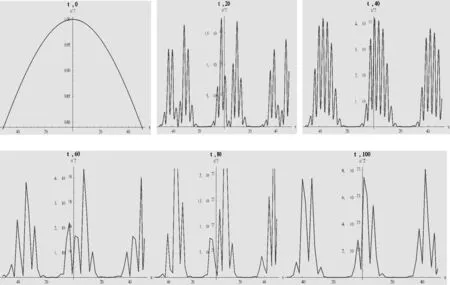
图6 |u|2与时间t的关系切片图

研究表明在正切周期势场中，由于外势场的奇异性导致了非线性薛定谔方程具有奇异性，并且具有类周期性。

参考文献：

[1]刘式适，刘式达.物理学中的非线性方程=Nonlinear Equationuations in Physics[M]．北京：北京大学出版社，2000.

[2]Govind P. Agrawal.贾东方,等译.非线性光纤光学原理及应用[M]．北京：电子工业出版社，2010.

[3]叶佩弦.非线性光学物理[M]．北京：北京大学出版社，2007.

[4]刘杰.玻色-爱因斯坦凝聚体动力学[M]．北京：科学出版社，2009.

[5]李帮庆，马玉兰.非线性发展方程与(G'/G)展开法[M]．北京：原子能出版社，2010.

[6]Robert W.Boyd. Nonlinear optics[M]．北京：世界图书出版社，2010.

[7]Gil Fanjoux, Jérémy Michaud, Hervé Maillotte, and Thibaut Sylvestre. Cascaded Raman slow light and optical spatial solitons in Kerr media[J].PRE.,2013,87:033838.

[8]Min Li, Jing-Hua Xiao, Wen-Jun Liu, Pan Wang, Bo Qin, and Bo Tian. Mixed-type vector solitons of the N-coupled mixed derivative nonlinear Schrödinger equations from optical fibers[J].PRE.,2013,87:032914.

[9]Franz G. Mertens, Niurka R. Quintero, A. R. Bishop. Nonlinear Schrödinger solitons oscillate under a constant external force[J].PRE,2013,87:032917.

[10]Justin T. Cole and Ziad H. Musslimani, Band gaps and lattice solitons for the higher-order nonlinear Schr?dinger equation with a periodic potential[J].PRA.,2014,90: 013815.