用于HJ-1-C卫星ScanSAR的等效RD几何校正方法

刘佳音 温双燕 张弘毅④ 洪 文

①(中国科学院空间信息处理与应用系统技术重点实验室 北京 100190)

②(微波成像技术国家重点实验室 北京 100190)

③(中国科学院电子学研究所 北京 100190)

④(中国科学院大学 北京 100049)

1 引言

HJ-1-C卫星是我国自主研制的第1颗民用合成孔径雷达卫星，它于2012年11月19日从太原卫星发射中心成功发射，其有效载荷为S波段SAR，具有全天时、全天候对地观测能力，可以获得5 m分辨率图像。HJ-1-C卫星与早前发射的环境一号A, B星组成环境与灾害检测预报的“小卫星星座”，从而可以对生态环境和灾害进行大范围、全天候、全天时动态检测，及时反映生态环境和灾害的发生，并对发展趋势进行预测，为灾害快速评估、救援和重建等工作提供重要科学数据。HJ-1-C卫星总重890 kg，轨道为500 km、降交点地方时上午6时的太阳同步轨道，使用6×2.8 m的可折叠式网状抛物面天线。HJ-1-C卫星SAR具有条带和扫描两种工作模式，成像带宽度分别为40 km和100 km。HJ-1-C的SAR雷达单视时空间分辨率可到5 m，距离向4视时分辨率为20 m，提供的SAR图像以多视模式为主[1]。

自从SIR-C[2]和RADARSAT[3]实现扫描模式(即ScanSAR)以来，扫描模式几乎成为了标准的星载SAR成像模式，最新的RADARSAT-2[4]和TerraSAR-X[5]星载SAR都具有扫描模式。虽然扫描模式的成像分辨率较低，但具有几百公里的观测宽度，在海岸线监测、冰山监视、船只航行等方面具有广泛应用[6]。而实现几百公里宽幅SAR图像的高效高精度定位则是ScanSAR地面处理的重要工作之一。常规星载SAR几何定位方法主要有两大类，一种基于地面控制点的间接定位法，主要从和SAR图像对应的数字地图中选取一定数量的合适地面控制点(Ground Control Points, GCP)，基于有理函数模型[7]、共线方程[8]及严密模型[9]等构象模型进行匹配校正。另一种在没有任何地面控制点情况下，利用卫星平台的位置、速度以及姿态等系统参数，根据星载SAR成像几何关系，对斜距图像的每个像素进行直接定位。

通常ScanSAR模式的成像及定位流程是先采用SPECAN等算法对每burst部分数据进行成像，然后利用RD算法进行定位校正，最后根据每burst校正后图像的地理位置进行拼接，获得全幅ScanSAR地图图像。但由于SPECAN算法在距离校正时仅考虑了距离游走，且忽略距离徙动的空变性[10]，因此成像精度差，同时该定位后拼接的流程会增加一次在burst之间重叠区域的重采样，不但降低效率，而且导致图像质量下降。因此本文根据HJ-1-C卫星ScanSAR模式的工作特点，在ECS成像算法和传统斜距多普勒定位方法基础上，提出一种适用于ScanSAR的等效RD几何校正方法。首先根据方位时刻关系进行方位拼接，然后根据斜距关系拼接各个子带，接着拟合等效参数，进行斜距多普勒定位，最后实现ScanSAR图像的几何校正。

2 HJ-1-C卫星ScanSAR的成像处理

2.1 HJ-1-C卫星ScanSAR的工作特性

ScanSAR工作模式是星载SAR的宽观测带工作模式，它是牺牲一部分方位分辨率来获得宽观测带。图1给出了ScanSAR工作模式的空间几何关系。对于正侧视的情况，通过天线在距离向的扫描来合成雷达图像，从而使观测带加宽。对于不同波束位置(简称波位)或称子观测带，ScanSAR工作模式是依次分别成像的。最初天线的波束指向宽观测带的近端并在那里驻留足够长的时间以合成1幅单波束照射区的雷达图像，然后天线波束在指向下一个位置以合成那里的雷达图像，依次类推，当卫星飞到最近端覆盖区的边缘时，天线波束指向宽观测带的最远端并合成那里的雷达图像，这时天线波束将指向最近端紧靠原来覆盖区的位置，并且开始第2次重复前面的过程。就是以这种方式，ScanSAR模式产生了一个加宽的雷达镶嵌图。

图1 ScanSAR工作原理几何关系Fig.1 Geometry for ScanSAR

HJ-1-C卫星的ScanSAR首先通过天线转动控制器，实现2845°°～的天线侧摆，同时SAR天线馈源阵共有12个馈源喇叭，相邻4个馈源形成1个波束，12个馈源由下而上依次共形成9个波束，通过大功率电子开关进行切换，进而获得覆盖2547°°～的视角范围。HJ-1-C卫星的ScanSAR共实现3组4波束扫描和5组3波束扫描方式，其基本参数如表1所示。

表1 HJ-1-C卫星的工作参数Tab.1 The radar parameters for HJ-1-C satellite

2.2 用于HJ-1-C卫星ScanSAR的ECS成像算法

针对ScanSAR成像特点，Moreira等人[11]根据正侧视距离模型提出Extended Chirp Scaling(ECS)算法，是CS的变形算法，在距离向通过修改CS因子，可以实现ScanSAR在距离向的自动配准，方位向则采用SPECAN算法完成聚焦。其处理框图如图2所示。

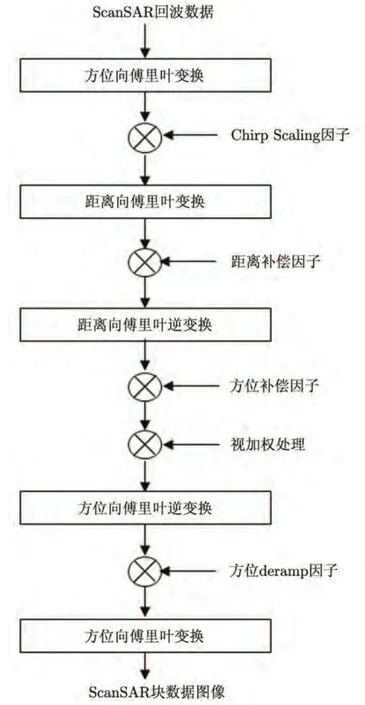
图2 ScanSAR的ECS算法流程图Fig.2 Functional flow diagram of ECS for ScanSAR

ECS算法主体类同于Chirp Scaling算法，其中距离向聚焦处理为匹配滤波，而方位向聚焦处理为谱分析方法。相应于方位向调频率去斜的谱分析方法，ECS算法首先进行方位加权因子的操作以完成方位向处理的旁瓣抑制；其次的Chirp Scaling操作、距离徙动校正、距离压缩、二次距离压缩同Chirp Scaling算法中的对应操作；方位补偿因子的操作用于校正由Chirp Scaling操作所带来的残余方位相差和方位信号的双曲相位去除；根据天线方向图，进行视加权处理；方位deramp因子实现方位去调频；最后经过多视处理完成ScanSAR成像处理。当ScanSAR块数据距离徙动量较大时，采用该方法进行成像处理，不仅能完全校正距离徙动，而且处理速度较快。

3 HJ-1-C卫星ScanSAR的几何校正

3.1 斜距多普勒定位模型

利用星历参数和SAR处理参数完成SAR图像定位的斜距-多普勒方法由斜距方程、多普勒中心频率方程、地球模型方程3个非线性方程组成[12]。

根据SAR精确测距的特点，建立SAR斜距图像的距离方程：

根据SAR多普勒频移成像的原理，建立SAR斜距图像的多普勒方程：

像点对应的物点位于地球表面，满足如下地球椭球方程：

其中：R表示卫星平台和目标点之间的斜距； Rs表示卫星平台位置矢量，表示目标点位置矢量，表示卫星平台速度矢量，表示目标点速度矢量； fdc表示多普勒中心频率；Re, Rp分别表示地球椭球模型的长半轴和短半轴，h表示地球高程。

3.2 用于HJ-1-C卫星ScanSAR的等效RD几何校正方法

斜距多普勒定位模型是基于基本雷达成像几何关系(即传统条带模式的几何关系)建立，而扫描模式与条带模式相比有较大区别，不同子带的波位参数均不相同，不能直接使用RD定位方法。通常用于扫描模式的几何校正方法一般对每个子带图像分别进行几何校正，然后再将若干组校正后的子带图像根据位置信息进行拼接。但是这种常规方法存在两个问题：(1)在子带图像几何校正和子带图像拼接时均需要进行图像重采样，不但效率低，而且多次图像插值影响图像质量；(2)由于不同子带图像的波位参数和系统误差不同，这样在重叠区子带图像根据位置信息不能完全重合，还需要进行匹配，不但降低处理效率，而且增加了处理难度。因此针对以上问题，本文提出了一种用于HJ-1-C卫星ScanSAR的高效率高精度的等效RD几何校正方法。首先对每个burst形成的图像分别进行方位向和距离向拼接，然后根据拼接后的ScanSAR图像进行等效参数计算，再代入斜距多普勒方程中，求解获得像素的地理位置，最后对整景ScanSAR图像进行重采样。

(1) 方位向拼接

同一观测带内的图像拼接和普通的条带式方位向拼接没有本质区别，只是必须考虑ScanSAR的时序关系。如图3所示，卫星每次飞行时在子观测带内的驻留时间为 Td, Tsyn为合成孔径时间， Tr为实际数据的保留长度。从图中可知，成像处理后的每个块数据图像方位向都包括3个部分：首 Td、中间Tsyn− Td和末 Td。其中只有中间部分是积累完整的点，可以保留。考虑到对于ScanSAR，要想获取方位向连续的图像，同一子观测带相邻块之间要有部分重叠，实际数据的保留长度为 Tr, Tr≤ Tsyn−Td。因此只要将块图像沿方位向在中间的 Tsyn− Td长数据中，以相同的方式截取长度为 Tr的数据，就能够保证图像的正确拼接。

(2) 距离向拼接

如图4所示，各子观测带的采样窗起点和采样窗终点分别为 TWbi和 TWei，因此相邻子观测带的重叠数据长度为：

考虑到相关运算和距离徙动校正的需要，必须有：

其中 Tp为脉冲宽度， Tm为最大距离徙动量。

在图像拼接时将处理得到的每个子观测带的图像沿距离向保留 TWei− TWbi− Trpi长度的数据，就可以用来进行图像拼接。

(3) 等效参数计算

由于每个子带的波位参数不相同，拼接后的ScanSAR图像不能直接使用雷达参数进行定位，需要根据成像处理过程中的参数，分别对等效脉冲重复频率、距离向像素间隔、近距、多普勒中心频率进行计算。

· 等效脉冲重复频率ePRF

其中， Vc为卫星飞行速度在地面分量， Sa为方位向标称分辨率。

· 距离向像素间隔Δr

其中， Clight是光速，N为距离向多视视数，在HJ-1-C卫星中设为4, fs为雷达采样频率。

· 近距 rnear

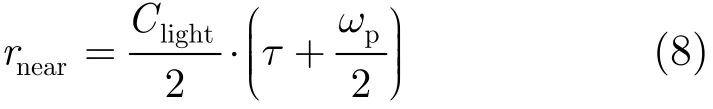
其中，τ为雷达采样延时，ωp为信号脉宽。

· 多普勒中心频率

多普勒中心频率根据成像处理中的每个子带多普勒中心频率和拼接后图像像素关系进行多项式拟合，一般为2次项：

其中，a0, a1, a2为拟合系数， ri为拼接后图像像素。

图3 同一子观测带相邻块之间的拼接时序关系Fig.3 Time series relationship of adjacent blocks in one burst

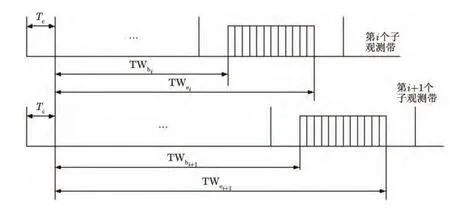
图4 相邻子观测带之间的拼接关系Fig.4 Mosaic relationship of adjacent bursts

4 HJ-1C卫星ScanSAR的几何校正处理流程

本文根据HJ-1C卫星ScanSAR模式的工作特点，在ECS成像算法和传统斜距多普勒定位方法基础上，提出一种适用于ScanSAR的等效RD几何校正方法。由于扫描模式的不同，子带的波位参数均不相同，而且同一子带的回波信号中间也有较长时间的“间断”，同一子带内相邻子块回波信号相位不衔接，因而首先对每一跳形成的子数据块进行ECS算法的成像处理和辐射校正，然后根据方位时刻关系进行同一观测带内的方位拼接，接着将各个子观测带图像按照斜距关系进行相邻子观测带之间的距离拼接，形成整景ScanSAR图像，之后利用成像处理的参数进行等效脉冲重复频率、距离向像素间隔、近距和多普勒中心频率的等效参数计算，并带入斜距多普勒方程进行定位，最后进行地图投影和图像重采样，获得一幅几何校正后的 ScanSAR图像。HJ-1C卫星ScanSAR的几何校正处理流程如图5所示。

5 实验

为验证本文算法的精度和效率，选取一组2013年3月18日在北京地区的HJ-1C卫星ScanSAR数据(编号MY_HJ1C_20130318_001828_S1_SAR_07360_06540)，该组数据对应的雷达参数如表 1，由4波束组成，具体参数如表2。首先进行ECS成像，然后对每burst进行方位向拼接和距离向拼接，接着根据成像过程中设定的参数分别计算等效参数，其结果如表3，最后在全幅ScanSAR图像上利用等效参数进行定位和校正。图6是经过ECS成像处理及方位和距离向拼接后的ScanSAR图像，图7是经过等效RD几何校正后的ScanSAR图像。本实验在校正后图像上均匀选取5个检查点，与Google Earth的参考影像图进行定位精度比较。表4给出了5个检查点的定位精度结果。

在24核Intel Xeon(CPU2.93 GHz)服务器计算节点上运行本文算法程序，上述一景图像成像处理用时72 s，几何校正用时10 s。

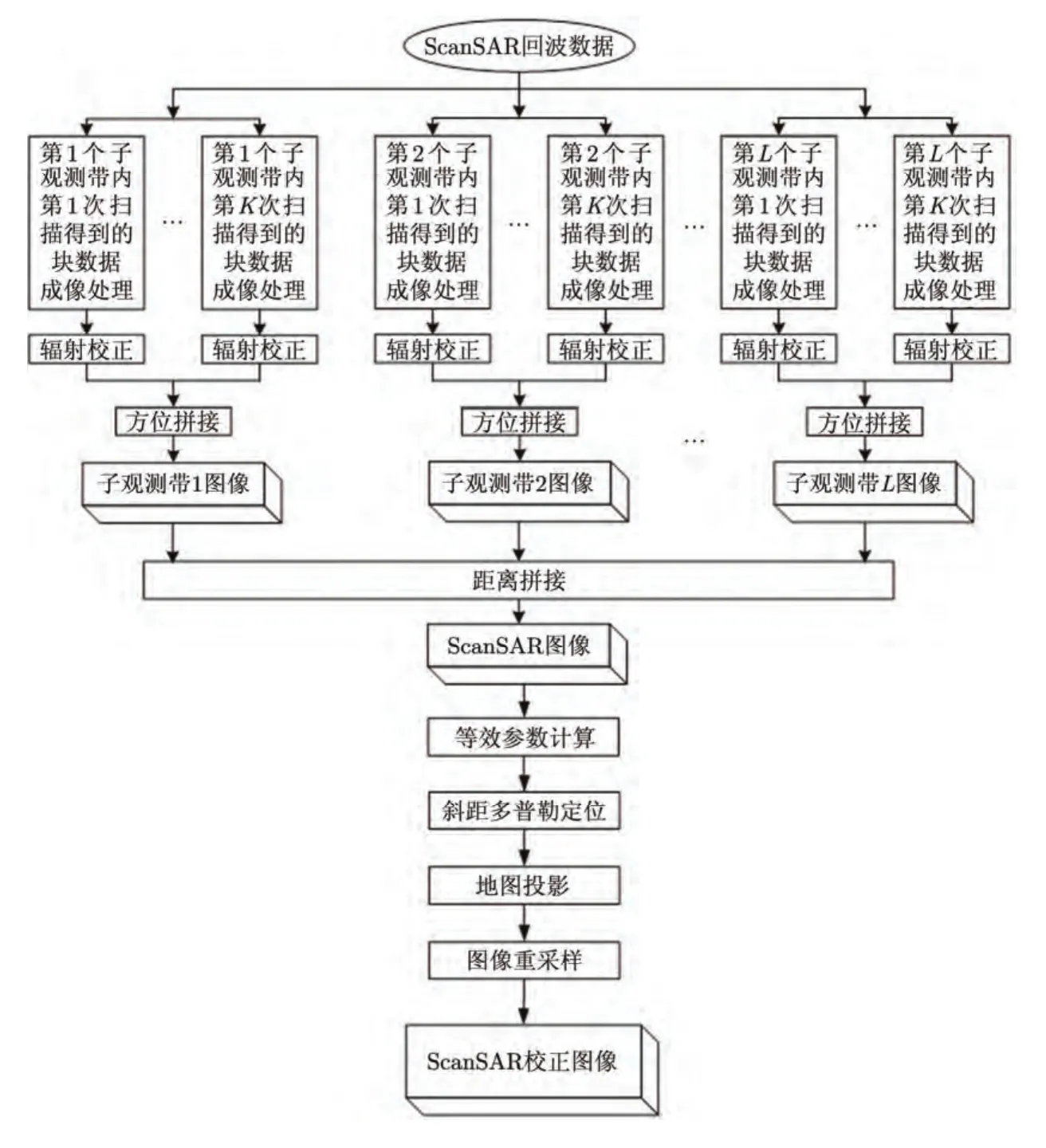
图5 HJ-1-C卫星ScanSAR的几何校正处理流程Fig.5 Geo-correct flow diagram of ScanSAR for HJ-1-C satellite

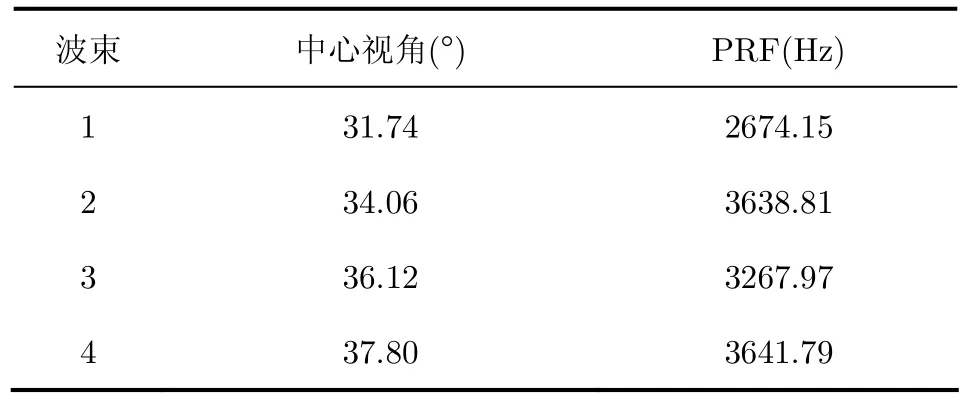
表2 HJ-1-C卫星ScanSAR (MY_HJ1C_20130318_001828 S1_SAR_07360_06540)波位参数Tab.2 The beam paramters of ScanSAR for HJ-1-C satellite(MY_HJ1C_20130318_001828_S1_SAR_07360_06540)

表3 等效参数计算结果Tab.3 The result of equivalent parameters

图6 成像处理及拼接后的ScanSAR图像Fig.6 ScanSAR image after image process and mosaic

图7 几何校正后的ScanSAR图像Fig.7 ScanSAR image after geo-correct

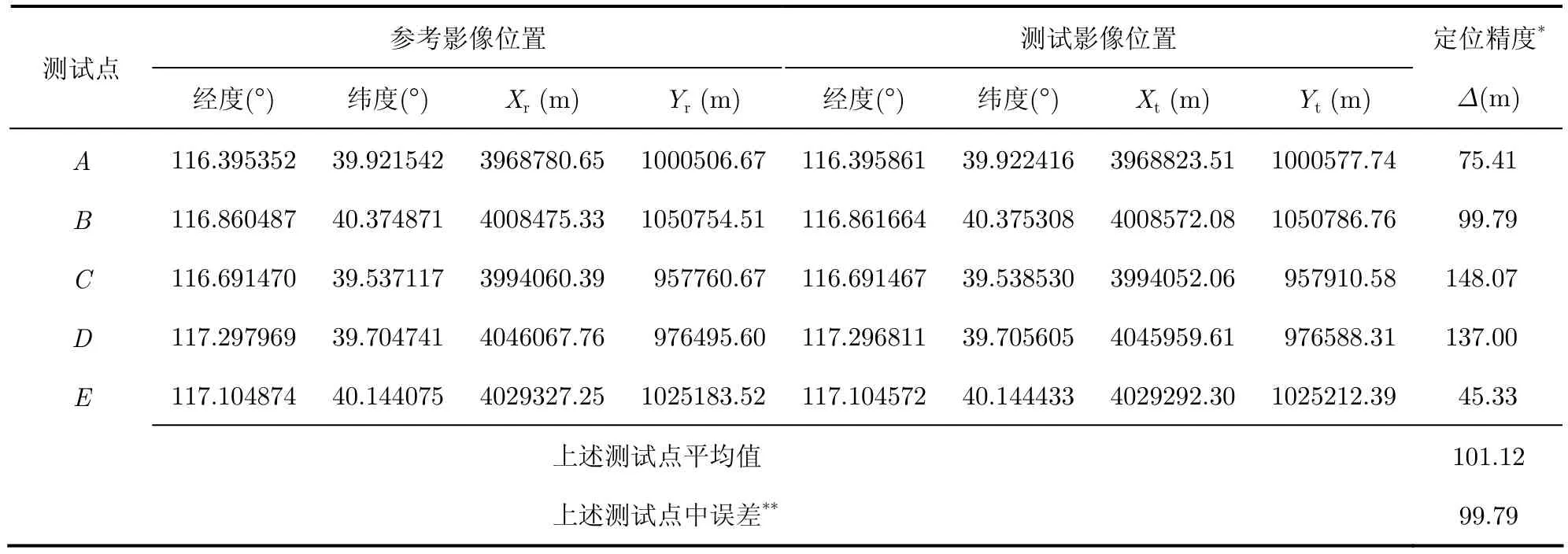
表4 HJ-1-C卫星ScanSAR (20130318)的几何定位精度Tab.4 The geolocation precision of ScanSAR for HJ-1-C satellite (20130318)

6 结论

通过对以上HJ-1-C卫星实际数据的处理实验，可以看出本文提出的等效RD几何校正方法，不但根据时序关系对 ScanSAR进行有效的方位向和距离向拼接，而且通过等效参数计算，将RD定位模型引入ScanSAR模式的定位中，保证了定位精度。通过实际数据结果表明：

(1) HJ-1-C卫星的ScanSAR模式在北京地区定位精度中误差为100 m；

(2) 在24核Intel Xeon服务器环境下，可以10 s完成一景ScanSAR图像的几何校正。

[1]王毅.环境一号C雷达卫星[J].卫星应用, 2012, (5): 74.Wang Yi.HJ-1-C radar satellite[J].Satellite Application,2012, (5): 74.

[2]Freeman A, Cruz J, Chapman B, et al..Calibration of SIR-C data products[C].IEEE Geoscience and Remote Sensing Symposium (IGARSS), Firenze, July 10-14, 1995: 1585-1587.

[3]Satish S, Stephane C, and Stephanie M.The RADARSAT-1 imaging performance, 14 years after lauch, and independent report on RADARSAT-2 image quality[C].IEEE Geoscience and Remote Sensing Symposium (IGARSS’2010), Honolulu,HI, July 25-30, 2010: 3458-3461.

[4]Touzi R, Hawkins R K, and Cote S. High-precision assessment and calibration of polarimetric RADARSAT-2 SAR using transponder measurements[J].IEEE Transactions on Geoscience and Remote Sensin g, 2013, 51(1): 487-503.

[5]Giustarini L, Hostache R, Matgen P, et al..A change detection approach to flood mapping in urban areas using TerraSAR-X[J].IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(4): 2417-2430.

[6]魏钟铨.合成孔径雷达卫星[M].北京: 科学出版社, 2001: 162.Wei Zhong-quan.Synthetic Aperture Radar Satellite[M].Beijing: Science Press, 2001: 162.

[7]魏晓红, 张路, 贺雪艳, 等.基于有理函数模型的星载SAR影像几何校正[J].遥感学报, 2012, 16(5): 1089-1099.Wei Xiao-hong, Zhang Lu, He Xue-yan, et al..Spaceborne SAR image geocoding with RFM model[J].J ournal ofRemote Sensing, 2012, 16(5): 1089-1099.

[8]尤红建, 丁赤飚, 付琨.SAR图像对地定位的严密共线方程模型[J].测绘学报, 2007, 36(2): 158-162.You Hong-jian, Ding Chi-biao, and Fu Kun.SAR image localization using rigorous SAR collinearity equation model[J].Acta Geodaetica et Cartographica Sinica, 2007,36(2): 158-162.

[9]刘佳音, 尤红建, 洪文.用于星载 SAR 图像几何校正的稀疏控制点修轨方法[J].武汉大学学报(信息科学版), 2013, 38(3):262-265.Liu Jia-yin, You Hong-jian, and Hong Wen.Modified orbit algorithm with sparse ground control points for georectification of space-borne SAR image[J].Geomatics and Information Science of Wuhan University, 2013, 38(3): 262-265.

[10]李春升, 杨威, 王鹏波.星载SAR成像处理算法综述[J].雷达学报, 2013, 2(1): 111-122.Li Chun-sheng, Yang Wei, and Wang Peng-bo.A review of spaceborne SAR algorithm for image formation[J].Journal of Radars, 2013, 2(1): 111-122.

[11]Moreira A, Mittermayer J, and Scheiber R.Extended chirp scaling algorithm for air- and spaceborne SAR data processing in stripmap and ScanSAR imaging modes[J].IEEE Transactions on Geoscience and Remote Sensing, 1996,34(5): 1123-1136.

[12]Curlander J C.Location of spaceborne SAR imagery[J].IEEE Transactions on Geoscience and Remote Sensing, 1982,20(3): 359-364.